交差検証

ythonとscikit-learnを使用して交差検証を行う基本的なコードを以下に示します。

この例では、K-Fold交差検証を使用します。

また、結果をグラフ化するためにmatplotlibを使用します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

from sklearn.datasets import load_iris
from sklearn.model_selection import cross_val_score
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import numpy as np

# データセットのロード
iris = load_iris()
X, y = iris.data, iris.target

# 分類器のインスタンス化
clf = DecisionTreeClassifier(random_state=1234)

# 交差検証のスコアを計算
scores = cross_val_score(clf, X, y, cv=5)

# スコアの平均と標準偏差を計算
mean_score = np.mean(scores)
std_dev = np.std(scores)
print(f"Average score: {mean_score}")
print(f"Standard deviation: {std_dev}")

# 結果のグラフ化
plt.bar(range(1, len(scores) + 1), scores)
plt.ylim([0.0, 1.0])
plt.xlabel('Fold')
plt.ylabel('Accuracy')
plt.title('Cross-validation scores')
plt.show()

このコードは、Irisデータセットを使用して決定木分類器の交差検証を行います。

cross_val_score関数は、分類器、特徴量、ターゲット、および分割数（この場合は5）を引数に取り、各分割に対するスコアの配列を返します。

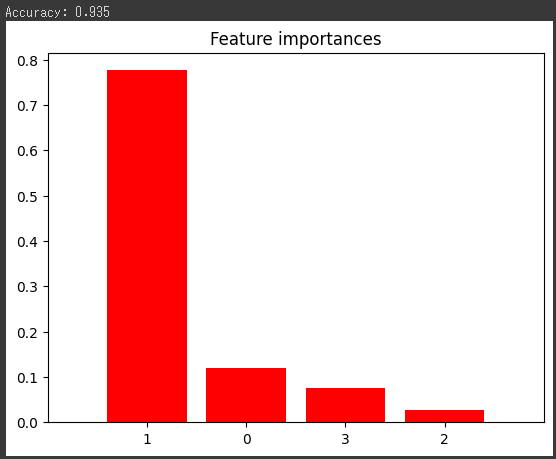
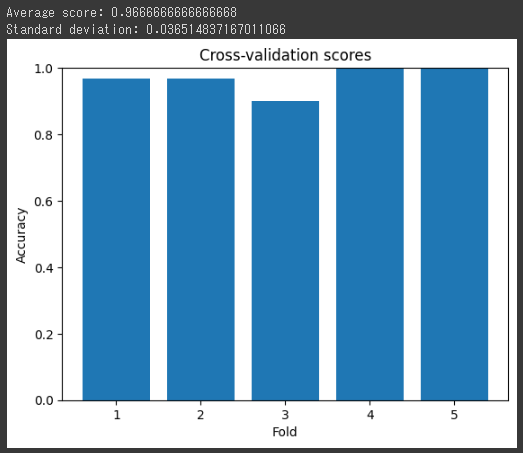
最後に、各分割のスコアを棒グラフで表示します。

これにより、モデルのパフォーマンスがどの程度一貫しているか（つまり、分割によって大きく変動しないか）を視覚的に確認できます。

[実行結果]

コード解説

このコードは、scikit-learnを使用して決定木分類器を交差検証するためのサンプルコードです。

以下にコードの詳細を説明します。

1行目から5行目:

必要なモジュールと関数をインポートします。
load_iris関数は、Irisデータセットをロードするために使用されます。
cross_val_score関数は、指定した分類器とデータセットで交差検証を行い、スコアを計算します。DecisionTreeClassifierは、決定木分類器のクラスです。
matplotlib.pyplotモジュールは、グラフの可視化のために使用されます。
numpyモジュールは、数値計算をサポートするために使用されます。

8行目から9行目:

load_iris関数を使用してIrisデータセットをロードし、Xとyに特徴量とラベルを格納します。

12行目:

DecisionTreeClassifierをインスタンス化します。
random_stateパラメータは、再現性のために乱数生成器のシードを設定します。

15行目:

cross_val_score関数を使用して交差検証のスコアを計算します。
cross_val_score関数は、指定された分類器とデータセットを使用して、指定された分割数（この場合は5）で交差検証を実行し、各分割のスコアを返します。
これらのスコアはscoresに格納されます。

18行目から21行目:

scoresの平均値と標準偏差を計算します。
np.mean関数はスコアの平均を計算し、np.std関数はスコアの標準偏差を計算します。
print関数では、平均スコアと標準偏差をコンソールに出力します。

24行目から29行目:

結果を棒グラフで可視化します。
plt.bar関数を使用して棒グラフを作成し、plt.ylimでy軸の範囲を設定します。
plt.xlabelとplt.ylabelでx軸とy軸のラベルを指定し、plt.titleでグラフのタイトルを設定します。
最後に、plt.showでグラフを表示します。

このコードは、Irisデータセットを使用して決定木分類器の交差検証を行い、結果を可視化する例です。

分類器やデータセットを変更することで、他の問題に対しても同様の手順を実行できます。

次元削減

次元削減の例題として、手書き数字の画像データセットであるMNISTを使用して、PCAを用いた次元削減を行う例を示します。

まず、Scikit-learnのデータセットモジュールからMNISTデータセットを読み込みます。

1
2
3
4
5
6

from sklearn.datasets import fetch_openml

# MNISTデータセットの読み込み
mnist = fetch_openml('mnist_784', version=1)
X = mnist.data
y = mnist.target

次に、読み込んだデータを正規化します。

1
2
3
4
5

from sklearn.preprocessing import MinMaxScaler

# 特徴量の正規化
scaler = MinMaxScaler()
X_normalized = scaler.fit_transform(X)

データを正規化した後、PCAを使用して次元削減を行います。

1
2
3
4
5

from sklearn.decomposition import PCA

# PCAのインスタンスを作成し、次元削減を実行
pca = PCA(n_components=2)
X_reduced = pca.fit_transform(X_normalized)

最後に、次元削減されたデータを可視化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

import matplotlib.pyplot as plt

# 可視化のためにデータを分割
x = X_reduced[:, 0]
y = X_reduced[:, 1]

# グラフのプロット
plt.scatter(x, y, c=y, cmap='viridis', alpha=0.5)
plt.colorbar(label='Digit')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.title('MNIST Dataset - PCA')

plt.show()

このコードを実行すると、次元削減されたデータを2次元平面上にプロットした散布図が表示されます。

各データポイントは手書き数字を表し、色によって異なる数字が示されます。

[実行結果]

この例では、MNISTデータセットを使用してPCAを適用し、高次元の手書き数字のデータを2次元に削減しました。

削減されたデータを散布図としてプロットすることで、異なる数字のパターンやクラスタを視覚化することができます。

ボストンの住宅価格予測

回帰問題の例として、ボストンの住宅価格データセットを使用して、部屋の数（RM）から住宅価格（MEDV）を予測する問題を考えてみましょう。

このデータセットは、scikit-learnライブラリに含まれています。

まず、必要なライブラリをインポートします。

1
2
3
4

import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

次に、データセットをロードします。

1

boston = datasets.load_boston()

部屋の数（RM）を特徴量として、住宅価格（MEDV）をターゲットとします。

1
2

X = boston.data[:, np.newaxis, 5]  # RM
y = boston.target  # MEDV

データを訓練セットとテストセットに分割します。

1
2
3
4

X_train = X[:-20]
X_test = X[-20:]
y_train = y[:-20]
y_test = y[-20:]

線形回帰モデルを作成し、訓練データで訓練します。

1
2

regr = linear_model.LinearRegression()
regr.fit(X_train, y_train)

テストデータを使って予測を行います。

1

y_pred = regr.predict(X_test)

結果を表示します。

1
2
3
4
5

print('Coefficients: \n', regr.coef_)
print('Mean squared error: %.2f'
      % mean_squared_error(y_test, y_pred))
print('Coefficient of determination: %.2f'
      % r2_score(y_test, y_pred))

最後に、結果をグラフ化します。

1
2
3
4
5
6

plt.scatter(X_test, y_test,  color='black')
plt.plot(X_test, y_pred, color='blue', linewidth=3)
plt.xlabel('Number of Rooms (RM)')
plt.ylabel('Median value of owner-occupied homes in $1000s (MEDV)')
plt.title('Linear Regression on Boston Housing Data')
plt.show()

このコードは、部屋の数から住宅価格を予測する線形回帰モデルを訓練し、その性能を評価し、結果をグラフ化します。

[実行結果]

ボストンの住宅価格の回帰の結果を評価するために、いくつかの指標が表示されました。

以下にそれぞれの指標の説明をします。

1. Coefficients: [9.126359]
これは、回帰モデルにおける説明変数（住宅価格を予測するための特徴量）の係数です。
単回帰の場合、この値は単一の特徴量の重みを示します。この場合、係数が9.126359と表示されています。

2. Mean squared error: 18.73
平均二乗誤差（Mean Squared Error, MSE）は、予測値と実際の値の間の差の二乗の平均です。
この値が小さいほど、モデルの予測が正確であることを示します。
この場合、MSEは18.73と表示されています。

3. Coefficient of determination: 0.20
決定係数（Coefficient of Determination）は、回帰モデルの予測の精度を示す指標です。
予測の精度は、実際の値の変動のうち、モデルがどれだけ説明できるかを表します。
決定係数の値は0から1の範囲であり、1に近いほど予測が正確です。
この場合、決定係数は0.20と表示されています。

この結果を解釈すると、係数は9.126359となっており、これは住宅価格の予測において重要な特徴量が1単位増加するごとに価格が約9.126359単位上昇することを示しています。

しかし、MSEが18.73となっているため、予測の誤差が比較的大きいことが分かります。

また、決定係数が0.20となっているため、このモデルは住宅価格の変動の約20％を説明できることを示しています。

ただし、この決定係数は予測の精度が低いことを意味しており、他の要素や特徴量がモデルに追加される必要があるかもしれません。

アンサンブル学習

アンサンブル学習の一つであるランダムフォレストを例に取り、scikit-learnを使って解説します。

ランダムフォレストは、複数の決定木を組み合わせて予測精度を向上させる手法です。

まず、必要なライブラリをインポートします。

1
2
3
4
5
6

import numpy as np
from sklearn.ensemble import RandomForestClassifier
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

次に、データセットを訓練データとテストデータに分割します。

make_classification関数を使用して、仮想的な分類データセットを生成します。

ここでは、n_samples=1000でサンプル数を指定し、n_features=4で特徴量の数を指定しています。

n_informative=2は、実際に予測に寄与する特徴量の数を指定し、n_redundant=0で冗長な特徴量の数を指定しています。

random_state=0でデータの乱数シードを固定し、shuffle=Falseでデータをシャッフルしないようにします。

1

X, y = make_classification(n_samples=1000, n_features=4, n_informative=2, n_redundant=0, random_state=0, shuffle=False)

ランダムフォレストのモデルを作成し、訓練データで学習させます。

train_test_split関数を使用してデータセットを訓練データとテストデータに分割します。

ここでは、訓練データが80%、テストデータが20%になるように分割しています。

1

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

ランダムフォレスト分類器（RandomForestClassifier）を作成し、訓練データで学習させます。

max_depth=2でツリーの深さを2に制限しています。

1
2

clf = RandomForestClassifier(max_depth=2, random_state=0)
clf.fit(X_train, y_train)

テストデータを使用して予測を行い、予測の正確さを評価します。

accuracy_score関数を使用して、実際のラベル（y_test）と予測されたラベル（y_pred）の一致率を計算し、表示します。

1
2

y_pred = clf.predict(X_test)
print("Accuracy:", accuracy_score(y_test, y_pred))

最後に、特徴量の重要度をグラフ化します。

ランダムフォレストモデルによって計算された特徴量の重要度を取得し、グラフ化して表示します。

importancesには各特徴量の重要度が格納され、indicesは重要度の降順で特徴量のインデックスが格納されます。

グラフはバー（縦棒）で表示され、各バーの高さは特徴量の重要度を表しています。

X軸は特徴量のインデックス、Y軸は重要度を表しています。

1
2
3
4
5
6
7
8
9

importances = clf.feature_importances_
indices = np.argsort(importances)[::-1]

plt.figure()
plt.title("Feature importances")
plt.bar(range(X.shape[1]), importances[indices], color="r", align="center")
plt.xticks(range(X.shape[1]), indices)
plt.xlim([-1, X.shape[1]])
plt.show()

[実行結果]

このグラフは、各特徴量がモデルの予測にどれだけ影響を与えているかを示しています。

高いバーは、その特徴量がモデルの予測に大きな影響を与えていることを示しています。

このグラフを通じて、モデルがどの特徴量を重要視しているかを理解することができます。

強化学習

強化学習の簡単な例題として、探索と利益のトレードオフを考慮したマルチアームバンディット問題を考えてみましょう。

以下に、サンプルデータを作成し、そのデータを元に最適化問題を解く方法を示します。

サンプルデータ:

• アーム1: 平均報酬1.5
• アーム2: 平均報酬2.0
• アーム3: 平均報酬1.8
• アーム4: 平均報酬1.2
• アーム5: 平均報酬1.7

また、最大の試行回数は100回とします。

以下が、CVXPYを使用してこの最適化問題を解くコード例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt

# アームの平均報酬
arm_means = [1.5, 2.0, 1.8, 1.2, 1.7]

# 最大の試行回数
max_trials = 100

# 変数の定義
x = cp.Variable(len(arm_means), boolean=True)

# 制約条件
constraints = [
    cp.sum(x) == 1,  # 1つのアームを選択する
    x >= 0          # 非負制約
]

# 目的関数
objective = cp.Maximize(cp.sum(cp.multiply(arm_means, x)))

# 最適化問題の定義
problem = cp.Problem(objective, constraints)

# 最適化の実行
optimal_value = problem.solve()

# 最適なアームの選択を取得
arm_selection = [i for i in range(len(arm_means)) if x.value[i] == 1][0]

# グラフ化
arms = range(len(arm_means))
rewards = [arm_means[i] for i in arms]
plt.bar(arms, rewards)
plt.xticks(arms)
plt.xlabel('Arm')
plt.ylabel('Average Reward')
plt.title('Average Reward of Arms')plt.show()

上記のコードでは、cvxpyライブラリを使用して最適化問題を定義しています。

目的関数は、選択したアームの平均報酬の総和を最大化するように設定されています。

制約条件として、1つのアームを選択することや非負制約を指定しています。

最適化問題を解くと、最適なアームの選択が得られます。

これをグラフ化することで、各アームの平均報酬を視覚的に理解することができます。

棒グラフでアームの番号に対応する平均報酬が表示されます。

[実行結果]

ソースコード解説

コードの各部分の説明をします。

1. import文:

• cvxpyモジュールをcpという別名でインポートしています。
  CVXPYは凸最適化問題を解くためのPythonライブラリです。
• numpyモジュールをnpという別名でインポートしています。
  NumPyは数値計算のためのPythonライブラリです。
• matplotlib.pyplotモジュールをpltという別名でインポートしています。
  Matplotlibはデータの可視化のためのPythonライブラリです。

2. データの定義:

• arm_meansは各アームの平均報酬を格納するリストです。
  例えば、[1.5, 2.0, 1.8, 1.2, 1.7]というリストは、5つのアームの平均報酬がそれぞれ1.5, 2.0, 1.8, 1.2, 1.7であることを示しています。
• max_trialsは最大の試行回数を表しています。

3. 変数の定義:

• xはアームの選択を表すバイナリ変数です。
  各要素が0または1の値を持ちます。
  この変数を使ってアームの選択を最適化します。

4. 制約条件の定義:

• constraintsは最適化問題の制約条件を表すリストです。
  ここでは、1つのアームを選択する制約(cp.sum(x) == 1)と非負制約(x >= 0)を設定しています。

5. 目的関数の定義:

• objectiveは最適化問題の目的関数を表すオブジェクトです。
  この場合、アームの平均報酬とアームの選択を乗算し、その総和を最大化するように設定しています。

6. 最適化問題の定義:

• problemは最適化問題を表すオブジェクトです。
  目的関数と制約条件を指定しています。

7. 最適化の実行:

• optimal_value = problem.solve()で最適化問題を解いています。
  最適化の結果、最適なアームの選択と最適な報酬の総和が得られます。

8. 最適なアームの選択を取得:

• arm_selectionは最適なアームの選択を示す変数です。
  アームの選択が1の要素のインデックスを取得しています。

9. グラフ化:

• armsはアームの番号を表すリストです。
• rewardsは各アームの平均報酬を格納したリストです。
• plt.bar()関数を使用してアームの番号に対応する平均報酬を棒グラフで表示しています。
• plt.xlabel()、plt.ylabel()、plt.title()で軸ラベルやタイトルを設定しています。
• plt.show()でグラフを表示します。

このコードの結果は、アームの平均報酬を棒グラフとして表示します。

最適なアームの選択結果と平均報酬が視覚化されます。

作物の収量予測

scikit-learnを使って、作物の収量予測を行ってみます。

作物の栽培に関するいくつかの特徴量（例：土壌のpH値、日照時間、降水量）と作物の収量の関係を持つサンプルデータセットを作成し、予測を行います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# サンプルデータの作成
np.random.seed(0)
n_samples = 100
X = np.random.rand(n_samples, 3)  # 特徴量：土壌のpH値、日照時間、降水量
y = 50 + 30 * X[:, 0] + 20 * X[:, 1] + 10 * X[:, 2] + 10 * np.random.randn(n_samples)  # 収量

# 線形回帰モデルの学習と予測
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)

# 結果の可視化
plt.figure(figsize=(10, 6))
plt.scatter(X[:, 0], y, color='b', label='Actual')
plt.scatter(X[:, 0], y_pred, color='r', label='Predicted')
plt.xlabel('soil pH value')
plt.ylabel('crop yield')
plt.title('Crop yield prediction')
plt.legend()
plt.show()

この例では、土壌のpH値が作物の収量に与える影響を考慮しています。

他の特徴量（日照時間、降水量）も同様に考慮できます。

グラフでは、実際の収量（青色の点）と予測された収量（赤色の点）が表示されます。

線形回帰モデルがデータに最適化され、実際の収量に近い予測を行うことが期待されます。

[実行結果]

ソースコード解説

このソースコードは、作物の収量予測を行うためにscikit-learnとmatplotlibを使用しています。

以下にソースコードの詳細を説明します。

1. ライブラリのインポート:

• numpyは数値計算を行うためのライブラリです。
• matplotlib.pyplotはデータの可視化を行うためのライブラリです。
• sklearn.linear_modelモジュールからLinearRegressionクラスをインポートしています。

2. サンプルデータの作成:

• np.random.seed(0)は乱数のシードを設定しています。
  これにより、再現可能な結果が得られます。
• n_samples = 100はサンプルの数を指定しています。
• X = np.random.rand(n_samples, 3)は、3つの特徴量（土壌のpH値、日照時間、降水量）を持つサンプルデータを作成しています。
• y = 50 + 30 * X[:, 0] + 20 * X[:, 1] + 10 * X[:, 2] + 10 * np.random.randn(n_samples)は、作物の収量を計算しています。特徴量と係数の線形結合に、ノイズとして正規分布からサンプリングした乱数を加えています。

3. 線形回帰モデルの学習と予測:

• model = LinearRegression()はLinearRegressionクラスのインスタンスを作成しています。
• model.fit(X, y)は作成したモデルにデータをフィットさせて学習を行います。
• y_pred = model.predict(X)は学習済みモデルを使用して入力データ X の収量を予測します。

4. 結果の可視化:

• plt.figure(figsize=(10, 6))はグラフの図のサイズを指定しています。
• plt.scatter(X[:, 0], y, color='b', label='Actual')は実際の収量を散布図で表示しています。
  X軸は土壌のpH値、Y軸は作物の収量です。
• plt.scatter(X[:, 0], y_pred, color='r', label='Predicted')は予測された収量を散布図で表示しています。
• plt.xlabel('soil pH value')はX軸のラベルを設定しています。
• plt.ylabel('crop yield')はY軸のラベルを設定しています。
• plt.title('Crop yield prediction')はグラフのタイトルを設定しています。
• plt.legend()は凡例を表示します。
• plt.show()はグラフを表示します。

このコードは、線形回帰モデルを使用して特徴量と作物の収量の関係を学習し、予測結果を可視化する例です。

特徴量には土壌のpH値だけでなく、他の特徴量も含めることができます。

院内感染の予測

医療データを使用して院内感染の予測や制御策の評価を行うためのサンプルを作成し、グラフ化します。

ここでは、以下の要素を考慮した仮想的なデータを使用します：

1. 患者の日次入院数
2. 感染症の発生数
3. 院内感染対策の強化レベル（0から10までのスケール）

まず、適切なライブラリをインポートします。

1
2
3
4

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

次に、仮想的なデータを作成します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

# 期間
days = np.arange(1, 31)

# ランダムな日次入院数の生成
admissions = np.random.randint(50, 150, size=len(days))

# ランダムな感染症の発生数の生成
infections = np.random.randint(0, 10, size=len(days))

# ランダムな院内感染対策の強化レベルの生成
precautions = np.random.randint(0, 10, size=len(days))

# データフレームの作成
data = pd.DataFrame({'Days': days, 'Admissions': admissions, 'Infections': infections, 'Precautions': precautions})

次に、線形回帰モデルを使用して、院内感染数と院内感染対策の強化レベルの関係を学習します。

1
2
3
4
5
6
7
8
9
10

# 特徴量とターゲットの定義
X = data[['Precautions']]
y = data['Infections']

# 線形回帰モデルの学習
model = LinearRegression()
model.fit(X, y)

# 予測値の計算
predictions = model.predict(X)

最後に、結果をグラフ化して可視化します。

1
2
3
4
5
6
7
8
9

# グラフの描画
plt.figure(figsize=(10, 6))
plt.scatter(data['Precautions'], data['Infections'], color='blue', label='Actual')
plt.plot(data['Precautions'], predictions, color='red', linewidth=3, label='Predicted')
plt.xlabel('Precautions')
plt.ylabel('Infections')
plt.title('Relationship between Precautions and Infections')
plt.legend()
plt.show()

このコードを実行すると、院内感染数と院内感染対策の強化レベルの関係を示すグラフが表示されます。

実際のデータポイントは青色で表示され、予測値は赤色の線で示されます。

[実行結果]

このグラフを通じて、院内感染対策の強化レベルが上がるにつれて、院内感染数が減少する傾向があるかどうかを確認することができます。

ソーシャルメディア分析

scikit-learnを使用して、ソーシャルメディアのコメントや投稿から感情分析を行い、その結果をグラフ化する例を提供します。

以下のコードは、サンプルデータを生成し、感情分析を実行して結果をグラフ化する方法を示しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

import numpy as np
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix

# サンプルデータの生成
np.random.seed(42)
comments = [
    "この映画は素晴らしいです！",
    "最悪の映画でした...",
    "絶対におすすめできません。",
    "興奮しました！",
    "つまらないストーリーでした。",
    "感動的な結末でした。",
]

labels = [1, 0, 0, 1, 0, 1]  # 1: positive, 0: negative

for _ in range(94):  # サンプルデータを100個に合わせる
    comment = "サンプルコメント"
    sentiment = np.random.randint(2)
    comments.append(comment)
    labels.append(sentiment)

# テキストデータを数値特徴に変換
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(comments)

# データセットをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, labels, test_size=0.2, random_state=42)

# ロジスティック回帰モデルの学習と予測
model = LogisticRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)

# 正解率の計算
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

# 混同行列の計算
cm = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(cm)

# 混同行列をグラフ化
labels = ['Negative', 'Positive']
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title("Confusion Matrix - Sentiment Analysis")
plt.colorbar()
tick_marks = np.arange(len(labels))
plt.xticks(tick_marks, labels, rotation=45)
plt.yticks(tick_marks, labels)
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
for i in range(len(labels)):
    for j in range(len(labels)):
        plt.text(j, i, str(cm[i, j]), ha='center', va='center', color='white')
plt.show()

このコードでは、追加の94個のサンプルデータを生成し、合計100個のデータセットを作成します。

その後、感情分析を実行して、正解率と混同行列が計算されます。最後に、混同行列がカラーマップを使用してグラフ化されます。

グラフは、x軸に予測ラベル（Negative、Positive）、y軸に真のラベル（Negative、Positive）を持つ混同行列を表示します。

グラフ上の各セルには、各カテゴリに分類されたコメントの数が表示されます。

[実行結果]

このグラフは、感情分析の結果を視覚化するために使用される混同行列を示しています。

x軸とy軸のラベルは予測されたラベル（Negative、Positive）と真のラベル（Negative、Positive）を示しています。各セルには、それぞれのラベルに分類されたコメントの数が表示されています。

例えば、左上のセルは真のラベルがNegativeであり、予測されたラベルもNegativeであるコメントの数を示しています。

同様に、右下のセルは真のラベルがPositiveであり、予測されたラベルもPositiveであるコメントの数を示しています。

このグラフを通じて、感情分析モデルの予測結果が真のラベルとどのように一致するかを可視化することができます。

クラスタリング

クラスタリング問題の一例として、顧客セグメンテーションを考えてみましょう。

この問題では、顧客の購買行動や属性に基づいて、顧客を異なるグループに分けることを目指します。

ここでは、年齢と年間購入額の2つの特徴を持つ顧客データを考えてみます。

まず、必要なライブラリをインポートします。

1
2
3

import matplotlib.pyplot as pltfrom
 sklearn.cluster import KMeans
import numpy as np

次に、仮想的な顧客データを作成します。

1
2
3
4
5

# 仮想的な顧客データを作成
np.random.seed(0)
age = np.random.normal(loc=40, scale=10, size=100)
annual_amount = np.random.normal(loc=50000, scale=15000, size=100)
X = np.column_stack((age, annual_amount))

このデータをKMeansクラスタリングを用いて分析します。

1
2

# KMeansクラスタリング
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)

最後に、結果をプロットします。

1
2
3
4
5
6

# クラスタリング結果をプロット
plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_)
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red')
plt.xlabel('Age')
plt.ylabel('Annual Amount')
plt.show()

このコードは、年齢と年間購入額に基づいて顧客を3つのクラスタに分けます。

そして、各クラスタの中心点を赤で表示します。これにより、顧客の購買行動のパターンを視覚的に理解することができます。

[実行結果]

このコードは仮想的なデータを使用していますので、実際の問題に適用する際には、適切なデータの前処理やパラメータの調整が必要になることに注意してください。

解説

ソースコードの内容を解説します。

1. 必要なライブラリのインポート:

• matplotlib.pyplot: データの可視化のためのライブラリ
• sklearn.cluster.KMeans: K-meansクラスタリングアルゴリズムの実装

2. 仮想的な顧客データの作成:

• age: 年齢データを平均40、標準偏差10の正規分布からランダムに生成
• annual_amount: 年間支出データを平均50000、標準偏差15000の正規分布からランダムに生成
• X: 年齢と年間支出を結合して特徴行列を作成

3. K-meansクラスタリングの実行:

• KMeans(n_clusters=3, random_state=0): クラスタ数を3に設定し、ランダムシードを0に設定してKMeansオブジェクトを作成
• fit(X): 特徴行列Xに対してクラスタリングを実行し、各サンプルのクラスタラベルを割り当てる

4. クラスタリング結果のプロット:

• plt.scatter(X[:, 0], X[:, 1], c=kmeans.labels_): 年齢をx軸、年間支出をy軸にし、各データポイントをクラスタラベルに基づいて散布図としてプロット
• plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s=300, c='red'): クラスタの中心点を赤い色でプロット
• plt.xlabel('Age')とplt.ylabel('Annual Amount'): x軸とy軸のラベルを設定
• plt.show(): グラフの表示

このコードは、仮想的な顧客データをK-meansクラスタリングアルゴリズムを使ってクラスタリングし、その結果を散布図として可視化します。

クラスタ数は3と設定されており、年齢と年間支出の2つの特徴量をもとに顧客をクラスタリングします。

クラスタリングの結果、各データポイントが所属するクラスタと、クラスタの中心点がプロットされます。

クロスセル予測

クロスセル予測は、顧客がある商品を購入した後に他の商品を購入する可能性を予測するための手法です。

ここでは、scikit-learnを使用して、顧客がある商品を購入した後に他の商品を購入する可能性を予測する簡単な例を示します。

1.ライブラリのインポート

これらのライブラリは、データの操作、可視化、モデルの訓練と評価に必要です。

1
2
3
4
5

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix

2.データの生成

ここでは、500人の顧客が商品Aを購入し、そのうち200人が商品Bも購入しているというデータを生成しています。

Xは顧客の特徴量を表し、yは商品Bを購入したかどうかを表します。

1
2
3
4
5
6
7
8
9
10
11
12

# 商品Aを購入した顧客の数
n_customers = 500

# 商品Aを購入した顧客のうち、商品Bも購入した顧客の数
n_cross_sell = 200

# 商品Aを購入した顧客の特徴量（ここではランダムに生成）
X = np.random.rand(n_customers, 10)

# 商品Bを購入したかどうかのラベル（最初のn_cross_sell人は1、残りは0）
y = np.zeros(n_customers)
y[:n_cross_sell] = 1

3.データの分割

データを訓練データとテストデータに分割します。

訓練データはモデルの学習に、テストデータはモデルの性能評価に使用します。

1
2

# データを訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

4.モデルの訓練

ランダムフォレスト分類器を使用してモデルを訓練します。

ランダムフォレストは、複数の決定木を組み合わせて予測を行うアルゴリズムです。

1
2
3
4
5

# ランダムフォレスト分類器のインスタンスを作成
clf = RandomForestClassifier(n_estimators=100, random_state=42)

# モデルを訓練
clf.fit(X_train, y_train)

5.予測と評価

訓練したモデルを使用してテストデータのクロスセルを予測し、混同行列を計算します。

混同行列は、モデルの性能を評価するための表です。

1
2
3
4
5

# テストデータのクロスセルを予測
y_pred = clf.predict(X_test)

# 混同行列を計算
cm = confusion_matrix(y_test, y_pred)

6.結果の可視化

混同行列をヒートマップとして表示します。

これにより、モデルの性能を視覚的に理解することができます。

1
2
3
4
5
6
7
8
9
10
11

# 混同行列を表示
plt.imshow(cm, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion matrix')
plt.colorbar()
tick_marks = np.arange(2)
plt.xticks(tick_marks, ['No Cross-sell', 'Cross-sell'], rotation=45)
plt.yticks(tick_marks, ['No Cross-sell', 'Cross-sell'])
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.show()

[実行結果]

実際の問題では、顧客の特徴量をより詳細に把握するために、購入履歴や顧客のデモグラフィック情報など、さまざまなデータを使用することがあります。

また、モデルの性能を向上させるために、パラメータのチューニングや他の機械学習アルゴリズムの使用もあります。

混同行列（Confusion Matrix）

モデルの予測結果は、混同行列（Confusion Matrix）によって表現されます。

混同行列は、実際のクロスセルのラベルと予測されたクロスセルのラベルを比較し、それらの関係を可視化します。

混同行列は4つのセルで構成されます：

• 真陽性（True Positive; TP）:
  実際のラベルが「クロスセルあり」であり、予測も「クロスセルあり」の場合。
• 真陰性（True Negative; TN）:
  実際のラベルが「クロスセルなし」であり、予測も「クロスセルなし」の場合。
• 偽陽性（False Positive; FP）:
  実際のラベルが「クロスセルなし」であり、予測が「クロスセルあり」となった場合。
• 偽陰性（False Negative; FN）:
  実際のラベルが「クロスセルあり」であり、予測が「クロスセルなし」となった場合。

混同行列の各セルには、実際のデータポイントの数が表示されます。

モデルが正しく予測した場合は真陽性（TP）や真陰性（TN）の数が高くなり、誤った予測があった場合は偽陽性（FP）や偽陰性（FN）の数が増えます。

この例では、混同行列が表示されると、x軸が予測ラベル、y軸が実際のラベルであり、それぞれのセルに該当するデータポイントの数が表示されます。

これにより、モデルの予測結果の正確さやエラーの傾向を評価することができます。

また、混同行列から算出される指標として、精度（Accuracy）、再現率（Recall）、適合率（Precision）、F1スコア（F1 Score）などがあります。

これらの指標は、モデルの性能評価や比較に使用されます。