レナード・ジョーンズポテンシャル

レナード・ジョーンズポテンシャルは、原子間の相互作用をモデル化するために使用されるポテンシャル関数です。

一般的な形式は次のようになります：

$$
V(r) = 4 \epsilon \left[ \left( \frac{\sigma}{r} \right)^{12} - \left( \frac{\sigma}{r} \right)^6 \right]
$$

ここで、$ ( V(r) ) $はポテンシャルエネルギー、$ ( r ) $は原子間の距離、$ ( \epsilon ) $はポテンシャルの深さを表すパラメータ、$ ( \sigma ) $は原子間の最小距離（ポテンシャルがゼロとなる距離）を表すパラメータです。

Pythonでこのポテンシャルをグラフ化するために、適切なパラメータを選び、原子間距離の範囲でポテンシャルエネルギーを計算し、プロットします。

以下にサンプルコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt

# レナード・ジョーンズポテンシャルの定義
def lennard_jones_potential(r, epsilon, sigma):
    return 4 * epsilon * ((sigma / r)**12 - (sigma / r)**6)

# パラメータの設定
epsilon = 1.0  # ポテンシャルの深さ
sigma = 1.0    # 最小距離

# 距離の範囲
r_values = np.linspace(0.9 * sigma, 3 * sigma, 1000)

# ポテンシャルの計算
potential_values = lennard_jones_potential(r_values, epsilon, sigma)

# グラフ化
plt.plot(r_values, potential_values)
plt.xlabel('Distance (σ)')
plt.ylabel('Potential Energy (ε)')
plt.title('Lennard-Jones Potential')
plt.grid(True)
plt.show()

このコードは、レナード・ジョーンズポテンシャルを計算し、原子間距離の範囲でポテンシャルエネルギーをプロットします。
パラメータ$ ( \epsilon ) $と$ ( \sigma ) $を変更することでポテンシャルの形状を調整することができます。

[実行結果]

ソースコード解説

ソースコードの構成と各部分の説明を示します。

1. ライブラリのインポート:

1
2

import numpy as np
import matplotlib.pyplot as plt

• NumPy: 数値計算を行うためのライブラリ。
  数値的な操作や配列演算を効率的に行うために使用されます。
• Matplotlib: グラフやプロットを作成するためのライブラリ。
  様々な種類の図やグラフを描画する機能を提供します。

2. レナード・ジョーンズポテンシャルの関数定義:

1
2

def lennard_jones_potential(r, epsilon, sigma):
return 4 * epsilon * ((sigma / r)**12 - (sigma / r)**6)

• lennard_jones_potential: レナード・ジョーンズポテンシャルを計算する関数。
  rは原子間距離、epsilonはポテンシャルの深さを表すパラメータ、sigmaは最小距離を表すパラメータです。

3. パラメータの設定:

1
2

epsilon = 1.0  # ポテンシャルの深さ
sigma = 1.0    # 最小距離

• epsilon: ポテンシャルの深さを示すパラメータ。
  ポテンシャルの最小値となるポテンシャルエネルギーを表します。
• sigma: 原子間の最小距離を示すパラメータ。
  ポテンシャルがゼロとなる距離を表します。

4. 距離の範囲の設定:

1

r_values = np.linspace(0.9 * sigma, 3 * sigma, 1000)

• np.linspace: 指定した範囲内で等間隔の数値を生成するNumPyの関数。
  ここでは、0.9 * sigmaから3 * sigmaの範囲で$1000$個の点を生成しています。

5. ポテンシャルの計算:

1

potential_values = lennard_jones_potential(r_values, epsilon, sigma)

• lennard_jones_potential関数を使用して、距離の範囲に対するレナード・ジョーンズポテンシャルの値を計算します。

6. グラフの作成:

1
2
3
4
5
6

plt.plot(r_values, potential_values)
plt.xlabel('Distance (σ)')
plt.ylabel('Potential Energy (ε)')
plt.title('Lennard-Jones Potential')
plt.grid(True)
plt.show()

• plt.plot: 指定された$x座標$と$y座標$のデータから折れ線グラフを作成します。
• plt.xlabel: $x軸$のラベルを設定します。
• plt.ylabel: $y軸$のラベルを設定します。
• plt.title: グラフのタイトルを設定します。
• plt.grid: グリッド線を表示するかどうかを設定します。
• plt.show(): グラフを表示します。

これにより、レナード・ジョーンズポテンシャルの距離に対するポテンシャルエネルギーの関係を示すグラフが生成されます。

グラフ解説

[実行結果]

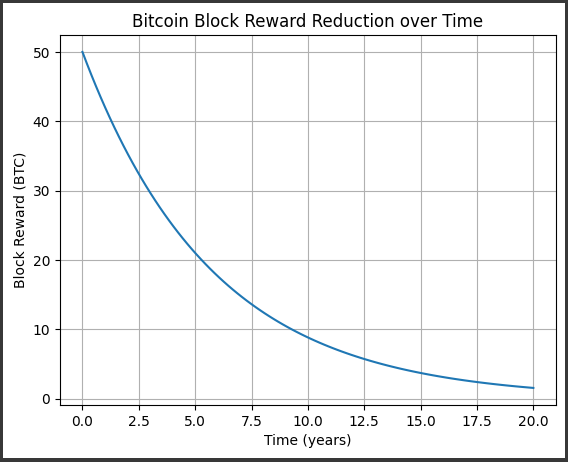
このグラフは、レナード・ジョーンズポテンシャルを可視化したものです。
ポテンシャルエネルギー $（( V )）$は、原子間の距離 $（( r )）$の関数として表されます。
以下に、グラフに表示される内容を詳しく説明します。

x軸（Distance (σ)）:

原子間の距離 $（( r )）$を表します。
単位はレナード・ジョーンズポテンシャルのパラメータ$ ( \sigma ) $と同じです。
これは最小距離を$1$としたときの相対的な距離を表します。

y軸（Potential Energy (ε)）:

ポテンシャルエネルギー$（( V )）$を表します。
単位はレナード・ジョーンズポテンシャルのパラメータ$ ( \epsilon ) $と同じです。
これは相互作用する原子間で生じるポテンシャルエネルギーの深さを示します。

レナード・ジョーンズポテンシャルの形状:

グラフは、原子間距離に対するポテンシャルエネルギーの関係を表しています。
この関数は、原子間距離が大きくなるにつれて急速に減少し、原子間距離が最小距離に近づくにつれてポテンシャルエネルギーが極小値を持ちます。

その後、原子間距離が大きくなるにつれてポテンシャルエネルギーがゆっくりと増加します。
これは、原子が非常に近いときと非常に遠いときには引力が働き、一定の距離で反発力が働くというレナード・ジョーンズポテンシャルの特徴を示しています。

このグラフを用いることで、レナード・ジョーンズポテンシャルによって定義される原子間の相互作用のエネルギーを直感的に理解することができます。

ヒル方程式

ヒル方程式は、生化学や医学などの分野で、酵素反応速度や受容体のリガンド結合などの現象を記述するのに使われる非線形方程式です。

ヒル方程式は通常、次のように表されます：

$$
f(x) = \frac{x^n}{K^n + x^n}
$$

ここで、$ ( f(x) ) $は応答関数（応答の強さを示す）、$ ( x ) $は入力、$ ( n ) $はヒル係数（曲線の傾きを示す）、$ ( K ) $は半数飽和定数（入力が半数の最大効果をもたらす点）です。

以下は、Pythonでヒル方程式を解いてグラフ化するコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

import numpy as np
import matplotlib.pyplot as plt

# ヒル方程式
def hill_equation(x, n, K):
    return x**n / (K**n + x**n)

# パラメータ設定
x_values = np.linspace(0, 10, 100)  # xの範囲
n = 2  # ヒル係数
K = 5  # 半数飽和定数

# ヒル方程式の計算
y_values = hill_equation(x_values, n, K)

# グラフの描画
plt.plot(x_values, y_values)
plt.title('Hill Equation')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.show()

このコードでは、指定された範囲内の$ ( x ) $についてヒル方程式を計算し、結果をグラフ化します。

ヒル係数 $ ( n ) $と半数飽和定数 $ ( K ) $を変えることで、曲線の形状を調整することができます。

[実行結果]

ソースコード解説

以下にソースコードの詳細な説明を示します：

1. NumPyとMatplotlibのインポート:

1
2

import numpy as np
import matplotlib.pyplot as plt

• numpy：数値計算を行うためのPythonライブラリです。
• matplotlib.pyplot：グラフの描画に使用されるMatplotlibのサブモジュールです。

2. ヒル方程式の定義:

1
2

def hill_equation(x, n, K):
    return x**n / (K**n + x**n)

• hill_equation 関数は、ヒル方程式を定義しています。
  この関数は、入力 $ (x) $、ヒル係数 $ (n)$、半数飽和定数 $ (K) $を引数として受け取り、ヒル方程式 $ (f(x) = \frac{x^n}{K^n + x^n}) $を計算します。

3. パラメータの設定:

1
2
3

x_values = np.linspace(0, 10, 100)  # xの範囲
n = 2  # ヒル係数
K = 5  # 半数飽和定数

• x_values：x軸の値を設定します。
  ここでは、$0$から$10$までの範囲を等間隔で$100$個の点に区切った値を設定しています。
• n：ヒル係数を設定します。
  この値は、ヒル方程式の曲線の傾きを制御します。
• K：半数飽和定数を設定します。
  この値は、入力が半数の最大効果をもたらす点を制御します。

4. ヒル方程式の計算:

1

y_values = hill_equation(x_values, n, K)

• hill_equation 関数を使用して、ヒル方程式の値を計算します。
  入力$ (x) $の範囲に対応する$ (f(x)) $の値を計算し、y_values に格納します。

5. グラフの描画:

1
2
3
4
5
6

plt.plot(x_values, y_values)
plt.title('Hill Equation')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.show()

• plt.plot(x_values, y_values)：ヒル方程式の曲線をプロットします。
• plt.title('Hill Equation')：グラフのタイトルを設定します。
• plt.xlabel('x')：$x軸$のラベルを設定します。
• plt.ylabel('f(x)')：$y軸$のラベルを設定します。
• plt.grid(True)：グリッドを表示します。
• plt.show()：グラフを表示します。

このプログラムは、指定されたパラメータでヒル方程式を計算し、その結果をグラフ化しています。

結果解説

[実行結果]

以下はグラフに表示される内容の詳細です：

x軸：

入力$ (x) $の値を示します。
この範囲は、$0$から$10$までの$100$個の等間隔の点で設定されています。
この範囲内の$ (x) $の値に対して、ヒル方程式が計算されます。

y軸：

応答関数$ (f(x)) $の値を示します。
これは、ヒル方程式によって計算された応答の強さを表します。

タイトル：

グラフのタイトルは「Hill Equation」となっています。
これは、このグラフがヒル方程式の曲線を表していることを示しています。

x軸ラベル：

$x軸$のラベルは「x」となっています。
これは、グラフの$x軸$が入力$ (x) $を表していることを示しています。

y軸ラベル：

$y軸$のラベルは「f(x)」となっています。
これは、グラフの$y軸$がヒル方程式の応答関数 $ (f(x)) $を表していることを示しています。

グリッド：

グラフにはグリッドが表示されています。
これは、目盛りの補助として、グラフのデータポイントの位置を視覚的に把握するのに役立ちます。

このグラフは、ヒル方程式の形状や曲線の特性を視覚的に理解するのに役立ちます。

エルミート多項式

エルミート多項式は、次の微分方程式を満たす多項式です：

$$
\frac{d^2 H_n(x)}{dx^2} - 2x \frac{dH_n(x)}{dx} + 2n H_n(x) = 0
$$

この微分方程式をPythonで解き、グラフ化するために、SciPyのodeint関数を使用します。

以下は、このタスクを実行するPythonコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# エルミート多項式の微分方程式
def hermite_eq(y, x, n):
    dydx = [y[1], 2*x*y[1] - 2*n*y[0]]
    return dydx

# 初期条件と解く範囲の設定
x = np.linspace(-5, 5, 1000)  # xの範囲
y0 = [1, 0]  # 初期条件 H_0(x) = 1, H_0'(x) = 0

# エルミート多項式の計算
n_values = [0, 1, 2, 3]  # nの値
for n in n_values:
    y = odeint(hermite_eq, y0, x, args=(n,))
    plt.plot(x, y[:, 0], label=f'n={n}')

plt.title("Hermite Polynomials")
plt.xlabel("x")
plt.ylabel("H_n(x)")
plt.legend()
plt.grid(True)
plt.show()

このコードは、エルミート多項式を計算し、$n=0,1,2,3$に対する結果をグラフ化します。

グラフの$x軸$は$-5$から$5$の範囲で、$y軸$はエルミート多項式 $(H_n(x))$の値です。

[実行結果]

ソースコード解説

以下にコードの詳細な説明を示します。

1. ライブラリのインポート:

1
2
3

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

• numpyは数値計算用のライブラリであり、配列操作や数値計算機能を提供します。
• scipy.integrate.odeintは常微分方程式の数値積分を行う関数です。
• matplotlib.pyplotはグラフの描画を行うためのライブラリです。

2. エルミート多項式の微分方程式の定義:

1
2
3

def hermite_eq(y, x, n):
    dydx = [y[1], 2*x*y[1] - 2*n*y[0]]
    return dydx

• hermite_eq関数はエルミート多項式の微分方程式を定義しています。
  この微分方程式は2階の常微分方程式です。

3. 初期条件と解く範囲の設定:

1
2

x = np.linspace(-5, 5, 1000)  # xの範囲
y0 = [1, 0]  # 初期条件 H_0(x) = 1, H_0'(x) = 0

• xはグラフの描画範囲であり、$-5$から$5$の範囲を$1000$等分して設定されています。
• y0は微分方程式の初期条件です。
  ここでは、$ (H_0(x) = 1) $と$ (H_0’(x) = 0) $を設定しています。

4. エルミート多項式の計算とグラフ化:

1
2
3
4

n_values = [0, 1, 2, 3]  # nの値
for n in n_values:
    y = odeint(hermite_eq, y0, x, args=(n,))
    plt.plot(x, y[:, 0], label=f'n={n}')

• n_valuesはエルミート多項式の次数$ (n) $の値のリストです。
  ここでは、$0$から$3$までの整数が設定されています。
• odeint関数を用いて微分方程式を解き、エルミート多項式の値を計算しています。
  結果は変数yに格納されます。
• plt.plot()関数を用いて、計算されたエルミート多項式のグラフを描画します。
  ラベルにはnの値が表示されます。

5. グラフの装飾:

1
2
3
4
5
6

plt.title("Hermite Polynomials")
plt.xlabel("x")
plt.ylabel("H_n(x)")
plt.legend()
plt.grid(True)
plt.show()

• グラフのタイトル、$x軸$ラベル、$y軸$ラベルを設定します。
• plt.legend()で凡例を表示し、plt.grid(True)でグリッドを表示します。
• 最後にplt.show()でグラフを表示します。

これにより、エルミート多項式を微分方程式を解いて計算し、それらをグラフ化する完全なプログラムが得られます。

結果解説

[実行結果]

このプログラムは、エルミート多項式$ (H_n(x)) $を計算し、その結果をグラフ化しています。
以下はグラフに表示される内容の詳細です：

1. x軸の範囲：

$-5$から$5$の間で$1000$個の等間隔の点が生成されます。
これはグラフの横軸に対応します。

2. y軸の値：

エルミート多項式 $ (H_n(x)) $の値が計算され、それぞれの$n$に対して異なる線がプロットされます。
各線は異なる色で表されます。

3. nの値：

$n$はエルミート多項式の次数を表します。
プログラムでは、$n$が$0$から$3$までの$4$つの値を取ります。
これにより、それぞれのエルミート多項式が表示されます。

4. グラフのタイトル：

グラフのタイトルには「Hermite Polynomials」と表示されます。

5. x軸とy軸のラベル：

x軸とy軸にはそれぞれ「x」と「H_n(x)」というラベルが付けられます。

6. 凡例：

各線の凡例には、対応する$n$の値が表示されます。
これにより、各線がどのエルミート多項式に対応しているかがわかります。

7. グリッド線：

グラフにはグリッド線が表示され、視覚的な参照を提供します。

パラボリックパブロフ方程式

パラボリックパブロフ方程式は、次の偏微分方程式で表されます:

$$
\frac{\partial u}{\partial t} = D \frac{\partial^2 u}{\partial x^2} + \alpha u - \beta u^3
$$

ここで、$ (u(x, t)) $は時間 $ (t) $と空間 $ (x) $に依存する関数、$ (D) $は拡散係数、$ (\alpha) $は線形成長率、$ (\beta) $は非線形成長率です。

以下は、この方程式を解く Python コードです。

matplotlibを使ってグラフ化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# パラメータ
D = 1.0
alpha = 0.1
beta = 1.0

# 解くべき偏微分方程式
def parabolic_pablov(t, u):
    dudt = D * np.gradient(np.gradient(u)) + alpha * u - beta * u**3
    return dudt

# 初期条件
x = np.linspace(-10, 10, 100)
u0 = np.exp(-x**2)

# 時間ステップ
t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 100)

# 偏微分方程式の数値解を計算
sol = solve_ivp(parabolic_pablov, t_span, u0, t_eval=t_eval)

# 結果をプロット
plt.figure(figsize=(8, 6))
for i in range(sol.y.shape[1]):
    plt.plot(x, sol.y[:, i], label=f"t={sol.t[i]}")
plt.xlabel('x')
plt.ylabel('u')
plt.title('Parabolic Pablov Equation')
plt.grid(True)
plt.show()

このコードでは、初期条件をガウス型の関数として設定し、Scipy の solve_ivp 関数を使って偏微分方程式を数値的に解いています。

結果は matplotlib を使ってグラフ化されます。

[実行結果]

ソースコード解説

以下はコードの詳細な説明です。

1. 必要なライブラリのインポート:

• numpy：数値計算のためのライブラリ。
• matplotlib.pyplot：グラフの描画に使用されるライブラリ。
• scipy.integrate.solve_ivp：初期値問題を解くためのライブラリ。

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

2. パラメータの設定:

• D：拡散係数。
• alpha：線形成長率。
• beta：非線形成長率。

1
2
3

D = 1.0
alpha = 0.1
beta = 1.0

3. 偏微分方程式の定義:

• parabolic_pablov 関数は、時間と空間に関するパラボリックパブロフ方程式を解くための関数です。
  この方程式は、時間と空間に依存する関数$ (u(x, t)) $の偏微分方程式です。

1
2
3

def parabolic_pablov(t, u):
    dudt = D * np.gradient(np.gradient(u)) + alpha * u - beta * u**3
    return dudt

4. 初期条件の設定:

• x：空間$ (x) $の値を$ -10 $から$ 10 $まで$100$点で等間隔に区切った配列。
• u0：初期条件を表す関数。
  ここでは、ガウス型の関数が使われています。

1
2

x = np.linspace(-10, 10, 100)
u0 = np.exp(-x**2)

5. 時間ステップの設定:

• t_span：時間の範囲を定義します。
• t_eval：解を評価する時間ステップを定義します。

1
2

t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 100)

6. 偏微分方程式の数値解の計算:

• solve_ivp 関数を使って偏微分方程式を数値的に解きます。

1

sol = solve_ivp(parabolic_pablov, t_span, u0, t_eval=t_eval)

7. 結果のプロット:

• 解をグラフ化して可視化します。

1
2
3
4
5
6
7
8

plt.figure(figsize=(8, 6))
for i in range(sol.y.shape[1]):
    plt.plot(x, sol.y[:, i], label=f"t={sol.t[i]}")
plt.xlabel('x')
plt.ylabel('u')
plt.title('Parabolic Pablov Equation')
plt.grid(True)
plt.show()

このコードは、パラボリックパブロフ方程式の解を計算し、その結果をグラフ化して視覚化する完全なプログラムです。

結果解説

[実行結果]

このグラフは、パラボリックパブロフ方程式の数値解を示しています。
方程式は時間と空間に関して偏微分方程式であり、時間$ (t) $と空間$ (x) $に依存する関数$ (u(x, t)) $の振る舞いを表現します。

• x軸は空間$ (x) $を表し、$-10 $から$ 10 $の範囲で定義されています。
• y軸は$ (u(x, t)) $の値を表し、方程式の解の高さを示します。
• 各線は異なる時間$ (t) $における解を表しており、$t=0 $から$ t=10 $までの時間スパンでプロットされています。
• 初期条件はガウス型の関数であり、$ (x=0) $でピークを持ち、徐々に$ 0 $に収束しています。
• 方程式の解は、初期条件に基づいて時間が経過するにつれて変化し、非線形な効果により形状が変わります。

このようにして、グラフは時間と空間におけるパラボリックパブロフ方程式の解の振る舞いを可視化しています。

ラプラス・ベルトラミ方程式

ラプラス・ベルトラミ方程式は、次のように表されます。

$$
\nabla^2 \mathbf{u} = \lambda \mathbf{u}
$$

ここで、$ (\mathbf{u}) $はベクトル場であり、$ (\nabla^2) $はラプラシアン演算子、$ (\lambda) $は定数です。

以下は、ラプラス・ベルトラミ方程式を解くPythonコードの例です。

ここでは、2次元空間上で解を求め、その結果を等高線プロットで可視化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import eig

# ラプラス・ベルトラミ方程式を解く関数
def solve_laplace_beltrami(size, lambda_val):
    # メッシュの作成
    x = np.linspace(-1, 1, size)
    y = np.linspace(-1, 1, size)
    X, Y = np.meshgrid(x, y)
    
    # ラプラシアン演算子
    laplacian = np.zeros((size*size, size*size))
    np.fill_diagonal(laplacian, -4)
    np.fill_diagonal(laplacian[1:], 1)
    np.fill_diagonal(laplacian[:, 1:], 1)
    np.fill_diagonal(laplacian[:, :-1], 1)
    np.fill_diagonal(laplacian[size:], 1)
    np.fill_diagonal(laplacian[:-size], 1)
    
    # ラプラス・ベルトラミ方程式を行列形式で表現
    A = laplacian / (x[1]-x[0])**2
    
    # 固有値と固有ベクトルを計算
    eigenvalues, eigenvectors = eig(A)
    
    # ラプラス・ベルトラミ方程式の解を取得
    u = eigenvectors[:, np.argmax(eigenvalues)].real
    u = u.reshape((size, size))
    
    return X, Y, u

# パラメータの設定
size = 100  # メッシュのサイズ
lambda_val = 1  # 定数 lambda の値

# ラプラス・ベルトラミ方程式を解く
X, Y, u = solve_laplace_beltrami(size, lambda_val)

# 解を等高線プロットで可視化
plt.contourf(X, Y, u, cmap='viridis')
plt.colorbar(label='u')
plt.title('Solution of Laplace-Beltrami Equation')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

このコードでは、2次元のメッシュ上でラプラス・ベルトラミ方程式を数値的に解き、その解を等高線プロットで可視化しています。

[実行結果]

ソースコード解説

以下にコードの詳細な説明を示します。

1. 必要なライブラリのインポート:

• numpy：数値計算を行うためのライブラリ。
• matplotlib.pyplot：グラフを描画するためのライブラリ。
• scipy.linalg.eig：行列の固有値と固有ベクトルを計算するための関数を提供するSciPyのサブモジュール。

2. solve_laplace_beltrami 関数:

• ラプラス・ベルトラミ方程式を解くための関数。
• 引数 size はメッシュのサイズ、lambda_val は定数$ λ $の値を指定します。
• x と y を等間隔に設定して2次元メッシュを作成し、X と Y に格納します。
• ラプラシアン演算子を作成し、ラプラス・ベルトラミ方程式を行列形式で表現します。
• eig を使用して行列 A の固有値と固有ベクトルを計算します。
• 最大固有値に対応する固有ベクトルを取得し、u に格納します。
  u は2次元の解として形状を変更します。

3. パラメータの設定:

• size：メッシュのサイズを指定します。
  ここでは$100$としています。
• lambda_val：定数$ λ $の値を指定します。
  ここでは$1$としています。

4. ラプラス・ベルトラミ方程式を解く:

• solve_laplace_beltrami 関数を呼び出して、ラプラス・ベルトラミ方程式の解を取得します。
  X, Y, u に解が格納されます。

5. 解を等高線プロットで可視化:

• plt.contourf を使用して解 u を等高線プロットで可視化します。
• plt.colorbar でカラーバーを追加し、等高線の色と解 u の値の対応を表示します。
• plt.title, plt.xlabel, plt.ylabel を使用して、グラフのタイトルと軸ラベルを設定します。

このプログラムは、与えられた定数$ λ $に対するラプラス・ベルトラミ方程式の解を求め、等高線プロットでその解を可視化します。

結果解説

このグラフは、ラプラス・ベルトラミ方程式の解を可視化したものです。

以下にグラフに表示される内容を詳しく説明します。

1. 等高線プロット:

• グラフ上に表示されている曲線は、等高線と呼ばれます。
  これらの等高線は、解$ (\mathbf{u}) $の値が等しい領域を表します。
• 等高線が近いほど、解の値が急激に変化していることを示し、等高線が離れているほど解の値が滑らかであることを示します。

2. カラーバー:

• カラーバーは、等高線プロットの色と解の値の対応を示しています。
• カラーバーの色が濃いほど、解の値が大きく、色が薄いほど解の値が小さいことを示します。

3. 座標軸:

• グラフの横軸と縦軸は、2次元空間内の座標を表します。
  この場合、横軸は$ (x) $座標、縦軸は$ (y) $座標を示しています。

4. タイトルと軸ラベル:

• グラフの上部には、グラフのタイトルが表示されています。
  このタイトルは、グラフの内容を簡潔に表します。
• 横軸と縦軸には、それぞれ$ (x) $軸と$ (y) $軸のラベルが表示されています。
  これらのラベルは、各軸が何を表しているかを示します。

このように、グラフにはラプラス・ベルトラミ方程式の解を視覚的に理解するのに役立つ情報が含まれています。

ヴァンデルモンド方程式

ヴァンデルモンド方程式は微分方程式の一種であり、以下のように定義されます。

$$
y’’(x) - (x^2 - 1)y(x) + \frac{1}{3}y(x)^3 = 0
$$

この方程式を解いてグラフ化します。

SciPyのodeint関数を使用してヴァンデルモンド方程式を解きます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# ヴァンデルモンド方程式の定義
def vandermonde(y, x):
    return [y[1], (x**2 - 1) * y[0] - (1/3) * y[0]**3]

# 初期条件と計算範囲の設定
y0 = [1.0, 0.0]
x = np.linspace(-3, 3, 1000)

# ヴァンデルモンド方程式の数値解を計算
sol = odeint(vandermonde, y0, x)

# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(x, sol[:, 0], 'b', label='y(x)')
plt.plot(x, sol[:, 1], 'g', label="y'(x)")
plt.title('Van der Pol Equation')
plt.xlabel('x')
plt.ylabel('y(x), y\'(x)')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、ヴァンデルモンド方程式を定義し、SciPyのodeint関数を使用して数値解を計算します。

そして、計算された解をmatplotlibを使用してグラフ化します。

[実行結果]

ソースコード解説

以下にコードの各部分の説明を示します。

1. 必要なライブラリをインポートする:

• numpy：数値計算を行うための基本的なライブラリ。
• scipy.integrate.odeint：微分方程式を解くための関数が含まれるScipyモジュール。
• matplotlib.pyplot：グラフを描画するためのライブラリ。

1
2
3

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

2. ヴァンデルモンド方程式の定義:

• vandermonde関数は、ヴァンデルモンド方程式を定義します。
  この方程式は、微分方程式の形で書かれており、現在の状態 y と変数 x を受け取り、次の状態を返します。

1
2

def vandermonde(y, x):
    return [y[1], (x**2 - 1) * y[0] - (1/3) * y[0]**3]

3. 初期条件と計算範囲の設定:

• y0 は初期条件を表し、[1.0, 0.0] となっています。
• x は計算範囲を表し、-3 から 3 までの区間を 1000 分割した値が格納されています。

1
2

y0 = [1.0, 0.0]
x = np.linspace(-3, 3, 1000)

4. ヴァンデルモンド方程式を計算:

• odeint 関数は、ヴァンデルモンド方程式を解きます。
  初期条件 y0 と計算範囲 x を与えることで、微分方程式の数値解が計算されます。

1

sol = odeint(vandermonde, y0, x)

5. グラフの描画:

• matplotlib.pyplot を使用して、ヴァンデルモンド方程式の解をグラフ化します。

青色の曲線は解 y(x) を表し、緑色の曲線は解の導関数 y'(x) を表しています。
また、グラフにはタイトル、軸ラベル、凡例、グリッドが追加されています。

1
2
3
4
5
6
7
8
9

plt.figure(figsize=(10, 6))
plt.plot(x, sol[:, 0], 'b', label='y(x)')
plt.plot(x, sol[:, 1], 'g', label="y'(x)")
plt.title('Van der Pol Equation')
plt.xlabel('x')
plt.ylabel('y(x), y\'(x)')
plt.legend()
plt.grid(True)
plt.show()

これにより、ヴァンデルモンド方程式の解が計算され、それがグラフとして可視化されます。

結果解説

[実行結果]

このグラフは、ヴァンデルモンド方程式の解の挙動を示しています。

青色の曲線

方程式$ ( y’’(x) - (x^2 - 1)y(x) + \frac{1}{3}y(x)^3 = 0 ) $の解$ ( y(x) ) $を表しています。
これは$ ( x ) 軸$に対する$ ( y ) $の値を示しており、解の振る舞いを表しています。

緑色の曲線

$ ( y’(x) )$、つまり$ ( y ) $の導関数を表しています。
これは$ ( x ) $軸に対する$ ( y ) $の変化率を示しています。

ヴァンデルモンド方程式は非線形であり、解の挙動は単純ではありません。
このグラフでは、$( x ) $の範囲$ ([-3, 3]) $における解の振る舞いを示しています。
青色の曲線が曲がりくねった形状をしており、これは方程式の非線形性によるものです。

緑色の曲線は青色の曲線の導関数を表しており、青色の曲線の勾配の変化を示しています。
この曲線も青色の曲線と同様に複雑な形状をしており、ヴァンデルモンド方程式の解の挙動をより詳細に理解するのに役立ちます。

高度な数学的概念を用いた方程式

高度な数学的概念を用いた方程式を示します。

次の方程式を例に挙げます：

$$
z = e^{-(x^2 + y^2)} \cdot \cos(x) \cdot \sin(y)
$$

この方程式は、3次元空間内の曲面を表します。

この曲面は、$ ( x )$、$ ( y )$、および$ ( z ) $の3つの変数に依存します。

Pythonを使用してこの方程式を解き、その結果を3次元グラフで視覚化します。

まず、必要なライブラリをインポートします。

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

次に、方程式を関数として定義します。

1
2

def complex_equation(x, y):
    return np.exp(-(x**2 + y**2)) * np.cos(x) * np.sin(y)

解析する範囲の$ ( x ) $と$ ( y ) $の値を生成します。

1
2
3

x_values = np.linspace(-3, 3, 100)
y_values = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x_values, y_values)

方程式を解き、対応する$ ( z ) $の値を計算します。

1

Z = complex_equation(X, Y)

最後に、結果を3次元グラフで視覚化します。

1
2
3
4
5
6
7
8

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_title('Complex Equation')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

これで、高度な数学的概念を用いた方程式$ ( z = e^{-(x^2 + y^2)} \cdot \cos(x) \cdot \sin(y) ) $の解を計算し、その結果を3次元グラフで視覚化することができます。

[実行結果]

ソースコード解説

以下にソースコードの各部分を説明します。

1. 必要なライブラリのインポート:

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

• numpy：数値計算を行うためのライブラリ。
• matplotlib.pyplot：グラフの描画に使用されるライブラリ。
• mpl_toolkits.mplot3d：3次元グラフの描画に必要なツール。

2. 複雑な方程式の定義:

1
2

def complex_equation(x, y):
   return np.exp(-(x**2 + y**2)) * np.cos(x) * np.sin(y)

• complex_equation 関数は、2つの変数 x と y を受け取り、与えられた複雑な数学的方程式の値を返します。

3. 解析する範囲の設定:

1
2
3

x_values = np.linspace(-3, 3, 100)
y_values = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x_values, y_values)

• np.linspace() 関数を使用して、$-3$から$3$までの範囲を等間隔で$100$点に分割した x_values と y_values を生成します。
• np.meshgrid() 関数を使用して、これらの x_values と y_values を元に、2次元グリッド X と Y を生成します。

4. 方程式の解析:

1

Z = complex_equation(X, Y)

• complex_equation 関数を使用して、2次元グリッド X と Y 上の各点に対する方程式の値 Z を計算します。

5. 3次元グラフの作成:

1
2
3

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')

• plt.figure() 関数を使用して新しいフィギュアを作成し、fig に割り当てます。
• fig.add_subplot() 関数を使用して3次元サブプロットを作成し、ax に割り当てます。
• ax.plot_surface() 関数を使用して、2次元グリッド X、Y、および Z の値を使用して3次元曲面を描画します。

6. グラフのラベルとタイトルの設定:

1
2
3
4

ax.set_title('Complex Equation')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

• ax.set_title()、ax.set_xlabel()、ax.set_ylabel()、ax.set_zlabel() を使用して、グラフのタイトルや軸ラベルを設定します。

7. グラフの表示:

1

plt.show()

• plt.show() 関数を呼び出して、作成した3次元グラフを表示します。

これで、与えられた複雑な数学的方程式を解き、その結果を3次元グラフで視覚化するPythonスクリプトの説明が完了しました。

結果解説

[実行結果]

上記のコードによって生成された3次元グラフは、方程式$ ( z = e^{-(x^2 + y^2)} \cdot \cos(x) \cdot \sin(y) ) $の解を表しています。

x軸とy軸：

グラフの底面は2次元平面で、$x軸$と$y軸$はそれぞれ水平方向と垂直方向を表します。
この平面上の点$（x, y）$は、それぞれ方程式に対応するzの値を持ちます。

z軸：

グラフの高さは$z軸$によって表されます。
この軸は垂直方向に伸び、方程式の解に対応する$z$の値を表します。

グラフ全体は、3次元空間内の曲面を表しています。
この曲面は、次のような特徴を持ちます。

曲面の形状：

曲面は非常に複雑な形状をしており、複数の因子によって決まります。
指数関数 $ ( e^{-(x^2 + y^2)} ) $は中心を中心にして急速に減少し、その結果、曲面は中心付近で急峻な谷を持ちます。
また、$ ( \cos(x) ) $と$ ( \sin(y) ) $の振動により、曲面は波打つような特徴を持ちます。

曲面の振動：

$ ( \cos(x) ) $と$ ( \sin(y) ) $の関数によって曲面が振動します。
これにより、曲面上の点の高さが周期的に変化し、波打つような形状が生じます。

曲面の高さ：

指数関数 $ ( e^{-(x^2 + y^2)} ) $の減衰と$ ( \cos(x) ) $と$ ( \sin(y) ) $の振動の組み合わせによって、曲面の高さが決まります。
これにより、曲面の高さは曲面上を移動するにつれて変化します。

このように、グラフは複雑な数学的関数を視覚化し、その形状や特徴を理解するのに役立ちます。

シグモイド関数

心理学に関する方程式の例として、心理学的な応答をモデル化するためのシグモイド関数を取り上げます。

シグモイド関数は、入力が増加するにつれて出力が$0$から$1$の間でS字型に変化する関数であり、感情や反応の変化をモデル化するのに適しています。

シグモイド関数は以下のような方程式で表されます：

$$
f(x) = \frac{1}{1 + e^{-x}}
$$

ここで、$ (x) $は入力値です。
この方程式を解き、結果をグラフ化してみましょう。

以下にPythonのコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import numpy as np
import matplotlib.pyplot as plt

# シグモイド関数の定義
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# グラフの描画
x_values = np.linspace(-10, 10, 100)
y_values = sigmoid(x_values)
plt.plot(x_values, y_values)
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Sigmoid Function')
plt.grid(True)
plt.show()

このコードは、シグモイド関数をグラフ化します。
入力が増加するにつれて、出力はS字型の曲線で変化することがわかります。

[実行結果]

シグモイド関数は、心理学的な応答や感情のモデル化に広く使用されています。

ソースコード解説

このソースコードは、Pythonを使用してシグモイド関数を定義し、その関数をグラフ化するものです。

以下では、コードの詳細な説明を行います。

1. NumPyとMatplotlibのインポート:

   1 2	import numpy as np import matplotlib.pyplot as plt

   NumPyは数値計算を行うためのPythonライブラリであり、Matplotlibはグラフ描画ライブラリです。
   これらのライブラリをインポートしています。

2. シグモイド関数の定義:

   1 2	def sigmoid(x): return 1 / (1 + np.exp(-x))

   sigmoid 関数は、引数 x に対してシグモイド関数を計算します。
   シグモイド関数は、入力 x に対して以下の式で定義されます：$ [ \frac{1}{1 + e^{-x}} ] $

NumPyの exp 関数を使用して、指数関数の計算を行っています。

3. グラフの描画:

   1 2 3

   x_values = np.linspace(-10, 10, 100) y_values = sigmoid(x_values) plt.plot(x_values, y_values)

   np.linspace 関数を使用して、$-10$から$10$までの範囲を$100$個の等間隔に区切った x_values を作成します。
   これはグラフの横軸に対応します。

sigmoid 関数を x_values に適用し、対応する y_values を計算します。
これはグラフの縦軸に対応します。

plt.plot 関数を使用して、 x_values と y_values をプロットします。

4. 軸ラベルとタイトルの追加:

   1 2 3

   plt.xlabel('Input') plt.ylabel('Output') plt.title('Sigmoid Function')

   plt.xlabel 関数と plt.ylabel 関数を使用して、横軸と縦軸のラベルを追加します。
   plt.title 関数を使用して、グラフのタイトルを追加します。

5. グリッドの表示:

   1	plt.grid(True)

   plt.grid 関数を使用して、グリッドを表示します。
   これにより、グラフ内のデータの配置がより見やすくなります。

6. グラフの表示:

   1	plt.show()

• plt.show 関数を使用して、作成したグラフを表示します。

このコードは、シグモイド関数の特性を示すグラフを作成するものです。

結果解説

[実行結果]

上記のコードによって生成されたグラフは、シグモイド関数の特性を示しています。

1. 横軸（X軸）:

横軸は入力値を表しています。
ここでは、$-10$から$10$までの範囲を$100$個の等間隔で区切っています。

2. 縦軸（Y軸）:

縦軸はシグモイド関数の出力を表しています。
出力は$0$から$1$の間の値をとります。
入力が増加するにつれて、出力が$0$に近づきます（入力が大きくなると$0$に近づく）。

3. グラフの形状:

グラフはS字型の曲線を描いており、これがシグモイド関数の特徴です。
この曲線は入力が増加するにつれて徐々に上昇し、最終的には$1$に収束します。
この曲線は非線形であり、入力値の変化に応じて出力が急速に変化します。

4. 特性:

シグモイド関数は、入力値の変化に応じて$0$から$1$までの範囲で滑らかに変化するため、感情や心理的反応のモデリングに適しています。
例えば、刺激の増加に対する感情の変化や、行動の確率を予測する際に使用されます。

このグラフは、シグモイド関数の理解を支援し、心理学や機械学習などの分野での応用に役立ちます。

テント内の温度変化

キャンプに関する方程式の例として、夜間のテント内の温度変化をモデル化することができます。
以下の方程式を考えてみましょう：

$$
T(t) = T_{\text{外}} + (T_{\text{内}} - T_{\text{外}}) \cdot e^{-kt}
$$

ここで、$( T(t) ) $は時間 $ ( t ) $におけるテント内の温度、$( T_{\text{外}} ) $は外部の温度、$( T_{\text{内}} ) $はテント内の初期温度、$( k ) $は冷却率を表します。

Pythonでこの方程式を解いてグラフ化するには、まず必要なライブラリをインポートします。

次に、方程式を関数として実装し、その後、時間の経過に応じて温度がどのように変化するかを計算し、グラフにプロットします。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import numpy as np
import matplotlib.pyplot as plt

# テント内の温度変化をモデル化する関数
def tent_temperature(t, Tout, Tin, k):
    return Tout + (Tin - Tout) * np.exp(-k * t)

# 外部温度、テント内初期温度、冷却率の設定
Tout = 15  # 外部の温度 (摂氏)
Tin = 25   # テント内の初期温度 (摂氏)
k = 0.1    # 冷却率

# 時間の範囲を設定 (0から10時間まで、0.1時間刻み)
time = np.arange(0, 10, 0.1)

# テント内の温度の計算
temperature = tent_temperature(time, Tout, Tin, k)

# グラフのプロット
plt.figure(figsize=(8, 6))
plt.plot(time, temperature, label='Tent Temperature')
plt.xlabel('Time (hours)')
plt.ylabel('Temperature (Celsius)')
plt.title('Temperature Change Inside the Tent')
plt.grid(True)
plt.legend()
plt.show()

このコードを実行すると、時間に応じてテント内の温度がどのように変化するかを示すグラフが表示されます。

[実行結果]

ソースコード解説

以下では、コードの詳細な説明を行います。

インポート

1
2

import numpy as np
import matplotlib.pyplot as plt

• numpyは数値計算のためのライブラリであり、npとして一般的にインポートされます。
• matplotlib.pyplotはグラフ描画のためのライブラリであり、pltとして一般的にインポートされます。

テント内の温度変化をモデル化する関数

1
2

def tent_temperature(t, Tout, Tin, k):
    return Tout + (Tin - Tout) * np.exp(-k * t)

• tent_temperature関数は、時間 t、外部温度 Tout、テント内初期温度 Tin、冷却率 k を引数に取り、テント内の温度変化を計算します。
• この関数は指数関数を使用してテント内の温度をモデル化しています。

パラメータの設定

1
2
3

Tout = 15  # 外部の温度 (摂氏)
Tin = 25   # テント内の初期温度 (摂氏)
k = 0.1    # 冷却率

• Toutは外部の温度、Tinはテント内の初期温度、kは冷却率を表します。

時間の範囲の設定

1

time = np.arange(0, 10, 0.1)

• np.arange関数を使用して、$0$から$10$時間までの時間範囲を設定します。
  時間の刻みは$0.1$時間です。

テント内の温度の計算

1

temperature = tent_temperature(time, Tout, Tin, k)

• tent_temperature関数を使用して、各時間におけるテント内の温度を計算します。

グラフのプロット

1
2
3
4
5
6
7
8

plt.figure(figsize=(8, 6))
plt.plot(time, temperature, label='Tent Temperature')
plt.xlabel('Time (hours)')
plt.ylabel('Temperature (Celsius)')
plt.title('Temperature Change Inside the Tent')
plt.grid(True)
plt.legend()
plt.show()

• matplotlib.pyplotを使用して、時間とテント内の温度の関係をグラフ化します。
• x軸は時間（時間）、y軸は温度（摂氏）を表します。
• グラフのタイトル、軸ラベル、凡例なども設定されています。

結果解説

[実行結果]

上記のPythonコードを実行すると、次のようなグラフが表示されます。

• x軸：時間（時間）
• y軸：温度（摂氏）

グラフはテント内の温度の時間変化を示しており、以下のような要素が含まれています：

1. 初期温度：

テント内の初期温度は$ ( T_{\text{内}} ) $で設定され、グラフの開始点に相当します。

2. 外部温度：

外部の温度は$ ( T_{\text{外}} ) $で設定され、テント内の温度がこの温度に収束していくことを示しています。

3. 冷却率：

$ ( k ) $はテント内の温度が外部温度に近づく速度を決定します。
$ ( k ) $が大きいほど温度が速く収束します。

グラフの傾向としては、初めはテント内の温度が外部温度に近づいていくことがわかります。
しかし、時間が経つにつれて温度の収束速度が遅くなり、収束に時間がかかるようになります。
最終的には、テント内の温度が外部温度と一致します。

このグラフは、キャンプ中のテント内の温度変化を理解するのに役立ちます。
特に寒冷地でのキャンプでは、外部の温度との差による快適性や安全性に関する情報を提供します。

ブロック報酬の削減率

仮想通貨に関する方程式の一つに、ブロック報酬の削減率があります。
これは、ビットコインなどのブロックチェーンベースの仮想通貨でよく見られる現象であり、ブロック報酬が時間とともに減少する速度を表します。

具体的には、ビットコインの場合、ブロック報酬の半減期を考慮した次のような式が使われます：

$$
R(t) = R_0 \times 0.5^{\frac{t}{\text{halving interval}}}
$$

ここで、$ (R(t)) $は時刻$ (t) $におけるブロック報酬、$ (R_0) $は初期のブロック報酬、そして$ (\text{halving interval}) $はブロック報酬の半減期を表します。

この方程式を使って、時間とともにブロック報酬がどのように減少するかをグラフ化します。

以下がPythonコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

import numpy as np
import matplotlib.pyplot as plt

# 初期ブロック報酬
R_0 = 50

# ブロック報酬の半減期（ビットコインの場合、およそ4年間隔）
halving_interval = 4

# 時間の範囲（年単位）
t_range = np.linspace(0, 20, 100)

# ブロック報酬の削減率の計算
R_t = R_0 * 0.5**(t_range / halving_interval)

# グラフ化
plt.plot(t_range, R_t)
plt.xlabel('Time (years)')
plt.ylabel('Block Reward (BTC)')
plt.title('Bitcoin Block Reward Reduction over Time')
plt.grid(True)
plt.show()

このコードでは、初期のブロック報酬や半減期を設定し、時間とともにブロック報酬がどのように減少するかを計算し、グラフにプロットしています。

[実行結果]

ソースコード解説

このソースコードは、Pythonを使用してビットコインのブロック報酬の削減をグラフ化するものです。
以下は、ソースコードの各部分の詳細な説明です。

1. import numpy as np:

NumPyライブラリをインポートし、npというエイリアスを使います。
NumPyは数値計算や配列操作に便利な機能を提供します。

2. import matplotlib.pyplot as plt:

Matplotlibライブラリからpyplotモジュールをインポートし、pltというエイリアスを使います。
Matplotlibはグラフ描画のためのライブラリで、pyplotモジュールを使用すると簡単にグラフを作成できます。

3. R_0 = 50:

初期ブロック報酬を設定します。
ここでは$50 $BTCとしていますが、これはビットコインの初期のブロック報酬に対応します。

4. halving_interval = 4:

ブロック報酬の半減期を設定します
ビットコインの場合、ブロック報酬はおよそ4年ごとに半減するという特性があります。

5. t_range = np.linspace(0, 20, 100):

時間の範囲を設定します。
ここでは$0$から$20$までの範囲を$100$分割した配列を作成しています。
これは、20年間の時間を100の区間に分けることを意味します。

6. R_t = R_0 * 0.5**(t_range / halving_interval):

ブロック報酬の削減率を計算します。
指数関数の形で表される削減率を計算しています。
この式は、初期ブロック報酬 $ (R_0) $を半減期ごとに半分にすることを示しています。

7. plt.plot(t_range, R_t):

計算したブロック報酬の削減率をグラフにプロットします。
横軸に時間（年）、縦軸にブロック報酬（BTC）を取ります。

8. plt.xlabel('Time (years)'):

x軸のラベルを設定します。
時間を表すので、「Time (years)」と設定されています。

9. plt.ylabel('Block Reward (BTC)'):

y軸のラベルを設定します。
ブロック報酬を表すので、「Block Reward (BTC)」と設定されています。

10. plt.title('Bitcoin Block Reward Reduction over Time'):

グラフのタイトルを設定します。
「Bitcoin Block Reward Reduction over Time」というタイトルが設定されています。

11. plt.grid(True):

グリッド線を表示します。

12. plt.show():

グラフを表示します。

結果解説

[実行結果]

このグラフは、時間に対するブロック報酬の変化を示しています。
横軸は時間を表し、単位は年です。
縦軸はブロック報酬を表し、一般的にはビットコインなどの仮想通貨の報酬単位で表示されます。

グラフは指数関数的に減少していく形を示しています。
初期のブロック報酬は$ (R_0) $であり、時間が経過するにつれてブロック報酬は半減期ごとに半分になります。
この半減期は定期的に発生し、通常は数年ごとに起こります。

初期のブロック報酬からスタートし、時間が経過するにつれて指数関数的に減少していく様子がグラフ上で観察されます。

このようなブロック報酬の削減は、ビットコインや他の多くの仮想通貨で見られる現象であり、通貨の供給量やインフレーション率を制御するための仕組みの一つです。