高度な数学的概念を用いた方程式

高度な数学的概念を用いた方程式

高度な数学的概念を用いた方程式を示します。

次の方程式を例に挙げます：

$$
z = e^{-(x^2 + y^2)} \cdot \cos(x) \cdot \sin(y)
$$

この方程式は、3次元空間内の曲面を表します。

この曲面は、$ ( x )$、$ ( y )$、および$ ( z ) $の3つの変数に依存します。

Pythonを使用してこの方程式を解き、その結果を3次元グラフで視覚化します。

まず、必要なライブラリをインポートします。

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

次に、方程式を関数として定義します。

1
2
def complex_equation(x, y):
    return np.exp(-(x**2 + y**2)) * np.cos(x) * np.sin(y)

解析する範囲の$ ( x ) $と$ ( y ) $の値を生成します。

1
2
3
x_values = np.linspace(-3, 3, 100)
y_values = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x_values, y_values)

方程式を解き、対応する$ ( z ) $の値を計算します。

1
Z = complex_equation(X, Y)

最後に、結果を3次元グラフで視覚化します。

1
2
3
4
5
6
7
8
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_title('Complex Equation')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

これで、高度な数学的概念を用いた方程式$ ( z = e^{-(x^2 + y^2)} \cdot \cos(x) \cdot \sin(y) ) $の解を計算し、その結果を3次元グラフで視覚化することができます。

[実行結果]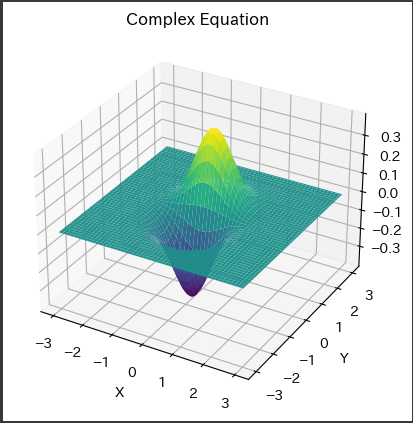

ソースコード解説

以下にソースコードの各部分を説明します。

1. 必要なライブラリのインポート:

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  • numpy：数値計算を行うためのライブラリ。
  • matplotlib.pyplot：グラフの描画に使用されるライブラリ。
  • mpl_toolkits.mplot3d：3次元グラフの描画に必要なツール。

2. 複雑な方程式の定義:

1
2
def complex_equation(x, y):
   return np.exp(-(x**2 + y**2)) * np.cos(x) * np.sin(y)
  • complex_equation 関数は、2つの変数 x と y を受け取り、与えられた複雑な数学的方程式の値を返します。

3. 解析する範囲の設定:

1
2
3
x_values = np.linspace(-3, 3, 100)
y_values = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x_values, y_values)
  • np.linspace() 関数を使用して、$-3$から$3$までの範囲を等間隔で$100$点に分割した x_values と y_values を生成します。
  • np.meshgrid() 関数を使用して、これらの x_values と y_values を元に、2次元グリッド X と Y を生成します。

4. 方程式の解析:

1
Z = complex_equation(X, Y)
  • complex_equation 関数を使用して、2次元グリッド X と Y 上の各点に対する方程式の値 Z を計算します。

5. 3次元グラフの作成:

1
2
3
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
  • plt.figure() 関数を使用して新しいフィギュアを作成し、fig に割り当てます。
  • fig.add_subplot() 関数を使用して3次元サブプロットを作成し、ax に割り当てます。
  • ax.plot_surface() 関数を使用して、2次元グリッド X、Y、および Z の値を使用して3次元曲面を描画します。

6. グラフのラベルとタイトルの設定:

1
2
3
4
ax.set_title('Complex Equation')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
  • ax.set_title()、ax.set_xlabel()、ax.set_ylabel()、ax.set_zlabel() を使用して、グラフのタイトルや軸ラベルを設定します。

7. グラフの表示:

1
plt.show()
  • plt.show() 関数を呼び出して、作成した3次元グラフを表示します。

これで、与えられた複雑な数学的方程式を解き、その結果を3次元グラフで視覚化するPythonスクリプトの説明が完了しました。

結果解説

[実行結果]

上記のコードによって生成された3次元グラフは、方程式$ ( z = e^{-(x^2 + y^2)} \cdot \cos(x) \cdot \sin(y) ) $の解を表しています。

x軸とy軸：

グラフの底面は2次元平面で、$x軸$と$y軸$はそれぞれ水平方向と垂直方向を表します。
この平面上の点$（x, y）$は、それぞれ方程式に対応するzの値を持ちます。

z軸：

グラフの高さは$z軸$によって表されます。
この軸は垂直方向に伸び、方程式の解に対応する$z$の値を表します。

グラフ全体は、3次元空間内の曲面を表しています。
この曲面は、次のような特徴を持ちます。

曲面の形状：

曲面は非常に複雑な形状をしており、複数の因子によって決まります。
指数関数 $ ( e^{-(x^2 + y^2)} ) $は中心を中心にして急速に減少し、その結果、曲面は中心付近で急峻な谷を持ちます。
また、$ ( \cos(x) ) $と$ ( \sin(y) ) $の振動により、曲面は波打つような特徴を持ちます。

曲面の振動：

$ ( \cos(x) ) $と$ ( \sin(y) ) $の関数によって曲面が振動します。
これにより、曲面上の点の高さが周期的に変化し、波打つような形状が生じます。

曲面の高さ：

指数関数 $ ( e^{-(x^2 + y^2)} ) $の減衰と$ ( \cos(x) ) $と$ ( \sin(y) ) $の振動の組み合わせによって、曲面の高さが決まります。
これにより、曲面の高さは曲面上を移動するにつれて変化します。

このように、グラフは複雑な数学的関数を視覚化し、その形状や特徴を理解するのに役立ちます。