ヴァンデルモンド方程式

ヴァンデルモンド方程式

ヴァンデルモンド方程式は微分方程式の一種であり、以下のように定義されます。

$$
y’’(x) - (x^2 - 1)y(x) + \frac{1}{3}y(x)^3 = 0
$$

この方程式を解いてグラフ化します。

SciPyのodeint関数を使用してヴァンデルモンド方程式を解きます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# ヴァンデルモンド方程式の定義
def vandermonde(y, x):
    return [y[1], (x**2 - 1) * y[0] - (1/3) * y[0]**3]

# 初期条件と計算範囲の設定
y0 = [1.0, 0.0]
x = np.linspace(-3, 3, 1000)

# ヴァンデルモンド方程式の数値解を計算
sol = odeint(vandermonde, y0, x)

# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(x, sol[:, 0], 'b', label='y(x)')
plt.plot(x, sol[:, 1], 'g', label="y'(x)")
plt.title('Van der Pol Equation')
plt.xlabel('x')
plt.ylabel('y(x), y\'(x)')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、ヴァンデルモンド方程式を定義し、SciPyのodeint関数を使用して数値解を計算します。

そして、計算された解をmatplotlibを使用してグラフ化します。

[実行結果]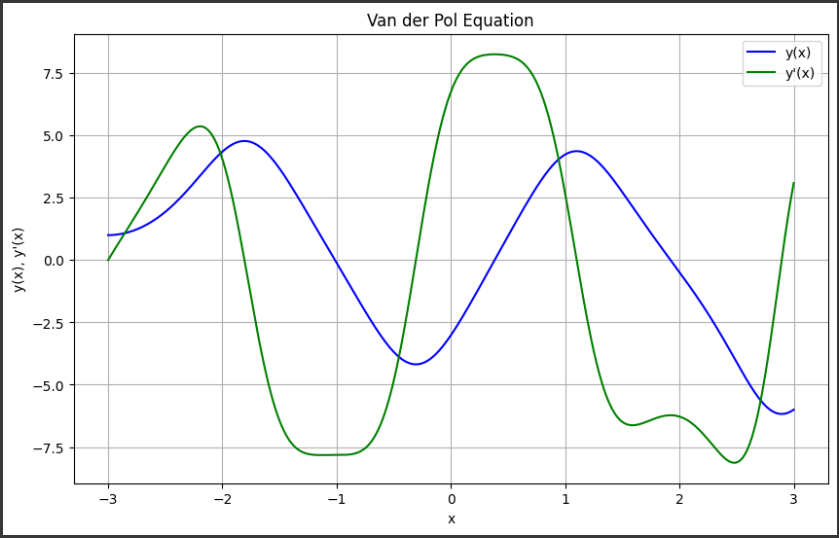

ソースコード解説

以下にコードの各部分の説明を示します。

1. 必要なライブラリをインポートする:

  • numpy：数値計算を行うための基本的なライブラリ。
  • scipy.integrate.odeint：微分方程式を解くための関数が含まれるScipyモジュール。
  • matplotlib.pyplot：グラフを描画するためのライブラリ。
1
2
3
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

2. ヴァンデルモンド方程式の定義:

  • vandermonde関数は、ヴァンデルモンド方程式を定義します。
    この方程式は、微分方程式の形で書かれており、現在の状態 y と変数 x を受け取り、次の状態を返します。
1
2
def vandermonde(y, x):
    return [y[1], (x**2 - 1) * y[0] - (1/3) * y[0]**3]

3. 初期条件と計算範囲の設定:

  • y0 は初期条件を表し、[1.0, 0.0] となっています。
  • x は計算範囲を表し、-3 から 3 までの区間を 1000 分割した値が格納されています。
1
2
y0 = [1.0, 0.0]
x = np.linspace(-3, 3, 1000)

4. ヴァンデルモンド方程式を計算:

  • odeint 関数は、ヴァンデルモンド方程式を解きます。
    初期条件 y0 と計算範囲 x を与えることで、微分方程式の数値解が計算されます。
1
sol = odeint(vandermonde, y0, x)

5. グラフの描画:

  • matplotlib.pyplot を使用して、ヴァンデルモンド方程式の解をグラフ化します。

青色の曲線は解 y(x) を表し、緑色の曲線は解の導関数 y'(x) を表しています。
また、グラフにはタイトル、軸ラベル、凡例、グリッドが追加されています。

1
2
3
4
5
6
7
8
9
plt.figure(figsize=(10, 6))
plt.plot(x, sol[:, 0], 'b', label='y(x)')
plt.plot(x, sol[:, 1], 'g', label="y'(x)")
plt.title('Van der Pol Equation')
plt.xlabel('x')
plt.ylabel('y(x), y\'(x)')
plt.legend()
plt.grid(True)
plt.show()

これにより、ヴァンデルモンド方程式の解が計算され、それがグラフとして可視化されます。

結果解説

[実行結果]

このグラフは、ヴァンデルモンド方程式の解の挙動を示しています。

青色の曲線

方程式$ ( y’’(x) - (x^2 - 1)y(x) + \frac{1}{3}y(x)^3 = 0 ) $の解$ ( y(x) ) $を表しています。
これは$ ( x ) 軸$に対する$ ( y ) $の値を示しており、解の振る舞いを表しています。

緑色の曲線

$ ( y’(x) )$、つまり$ ( y ) $の導関数を表しています。
これは$ ( x ) $軸に対する$ ( y ) $の変化率を示しています。

ヴァンデルモンド方程式は非線形であり、解の挙動は単純ではありません。
このグラフでは、$( x ) $の範囲$ ([-3, 3]) $における解の振る舞いを示しています。
青色の曲線が曲がりくねった形状をしており、これは方程式の非線形性によるものです。

緑色の曲線は青色の曲線の導関数を表しており、青色の曲線の勾配の変化を示しています。
この曲線も青色の曲線と同様に複雑な形状をしており、ヴァンデルモンド方程式の解の挙動をより詳細に理解するのに役立ちます。