ラプラス・ベルトラミ方程式

ラプラス・ベルトラミ方程式

ラプラス・ベルトラミ方程式は、次のように表されます。

$$
\nabla^2 \mathbf{u} = \lambda \mathbf{u}
$$

ここで、$ (\mathbf{u}) $はベクトル場であり、$ (\nabla^2) $はラプラシアン演算子、$ (\lambda) $は定数です。

以下は、ラプラス・ベルトラミ方程式を解くPythonコードの例です。

ここでは、2次元空間上で解を求め、その結果を等高線プロットで可視化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import eig

# ラプラス・ベルトラミ方程式を解く関数
def solve_laplace_beltrami(size, lambda_val):
    # メッシュの作成
    x = np.linspace(-1, 1, size)
    y = np.linspace(-1, 1, size)
    X, Y = np.meshgrid(x, y)
    
    # ラプラシアン演算子
    laplacian = np.zeros((size*size, size*size))
    np.fill_diagonal(laplacian, -4)
    np.fill_diagonal(laplacian[1:], 1)
    np.fill_diagonal(laplacian[:, 1:], 1)
    np.fill_diagonal(laplacian[:, :-1], 1)
    np.fill_diagonal(laplacian[size:], 1)
    np.fill_diagonal(laplacian[:-size], 1)
    
    # ラプラス・ベルトラミ方程式を行列形式で表現
    A = laplacian / (x[1]-x[0])**2
    
    # 固有値と固有ベクトルを計算
    eigenvalues, eigenvectors = eig(A)
    
    # ラプラス・ベルトラミ方程式の解を取得
    u = eigenvectors[:, np.argmax(eigenvalues)].real
    u = u.reshape((size, size))
    
    return X, Y, u

# パラメータの設定
size = 100  # メッシュのサイズ
lambda_val = 1  # 定数 lambda の値

# ラプラス・ベルトラミ方程式を解く
X, Y, u = solve_laplace_beltrami(size, lambda_val)

# 解を等高線プロットで可視化
plt.contourf(X, Y, u, cmap='viridis')
plt.colorbar(label='u')
plt.title('Solution of Laplace-Beltrami Equation')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

このコードでは、2次元のメッシュ上でラプラス・ベルトラミ方程式を数値的に解き、その解を等高線プロットで可視化しています。

[実行結果]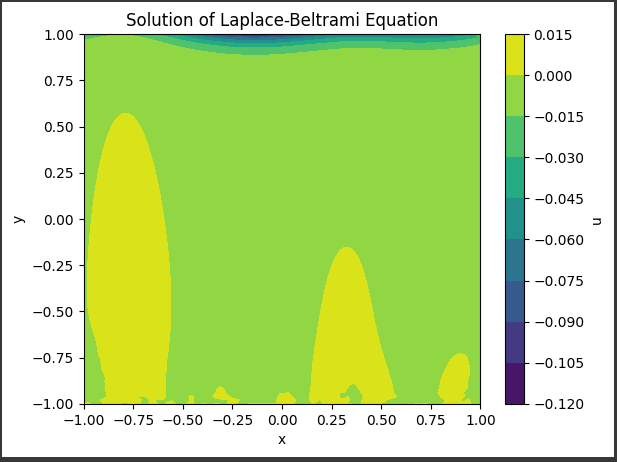

ソースコード解説

以下にコードの詳細な説明を示します。

1. 必要なライブラリのインポート:

  • numpy：数値計算を行うためのライブラリ。
  • matplotlib.pyplot：グラフを描画するためのライブラリ。
  • scipy.linalg.eig：行列の固有値と固有ベクトルを計算するための関数を提供するSciPyのサブモジュール。

2. solve_laplace_beltrami 関数:

  • ラプラス・ベルトラミ方程式を解くための関数。
  • 引数 size はメッシュのサイズ、lambda_val は定数$ λ $の値を指定します。
  • x と y を等間隔に設定して2次元メッシュを作成し、X と Y に格納します。
  • ラプラシアン演算子を作成し、ラプラス・ベルトラミ方程式を行列形式で表現します。
  • eig を使用して行列 A の固有値と固有ベクトルを計算します。
  • 最大固有値に対応する固有ベクトルを取得し、u に格納します。
    u は2次元の解として形状を変更します。

3. パラメータの設定:

  • size：メッシュのサイズを指定します。
    ここでは$100$としています。
  • lambda_val：定数$ λ $の値を指定します。
    ここでは$1$としています。

4. ラプラス・ベルトラミ方程式を解く:

  • solve_laplace_beltrami 関数を呼び出して、ラプラス・ベルトラミ方程式の解を取得します。
    X, Y, u に解が格納されます。

5. 解を等高線プロットで可視化:

  • plt.contourf を使用して解 u を等高線プロットで可視化します。
  • plt.colorbar でカラーバーを追加し、等高線の色と解 u の値の対応を表示します。
  • plt.title, plt.xlabel, plt.ylabel を使用して、グラフのタイトルと軸ラベルを設定します。

このプログラムは、与えられた定数$ λ $に対するラプラス・ベルトラミ方程式の解を求め、等高線プロットでその解を可視化します。

結果解説

このグラフは、ラプラス・ベルトラミ方程式の解を可視化したものです。

以下にグラフに表示される内容を詳しく説明します。

1. 等高線プロット:

  • グラフ上に表示されている曲線は、等高線と呼ばれます。
    これらの等高線は、解$ (\mathbf{u}) $の値が等しい領域を表します。
  • 等高線が近いほど、解の値が急激に変化していることを示し、等高線が離れているほど解の値が滑らかであることを示します。

2. カラーバー:

  • カラーバーは、等高線プロットの色と解の値の対応を示しています。
  • カラーバーの色が濃いほど、解の値が大きく、色が薄いほど解の値が小さいことを示します。

3. 座標軸:

  • グラフの横軸と縦軸は、2次元空間内の座標を表します。
    この場合、横軸は$ (x) $座標、縦軸は$ (y) $座標を示しています。

4. タイトルと軸ラベル:

  • グラフの上部には、グラフのタイトルが表示されています。
    このタイトルは、グラフの内容を簡潔に表します。
  • 横軸と縦軸には、それぞれ$ (x) $軸と$ (y) $軸のラベルが表示されています。
    これらのラベルは、各軸が何を表しているかを示します。

このように、グラフにはラプラス・ベルトラミ方程式の解を視覚的に理解するのに役立つ情報が含まれています。