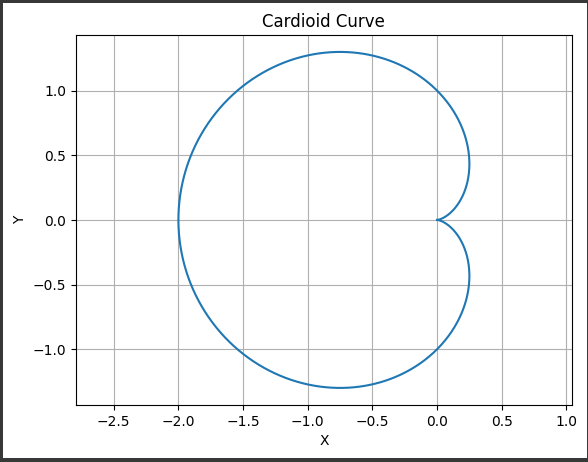
カーディオイド曲線

カーディオイド曲線

カーディオイド曲線は、数学的に興味深い図形のひとつで、心臓の形に似ていることからその名がついています。
以下にカーディオイド曲線の特徴と数学的な性質を説明します。

1. 数学的表現:

カーディオイド曲線の極座標方程式は以下のように表されます：
$$
r = a(1 - \cos(\theta))
$$
ここで、$( r ) $は極座標系における距離、$( \theta ) $は極座標系における角度、$( a ) $は定数です。

2. 形状:

カーディオイド曲線は、原点を中心とする座標系において、放射状に伸びる葉っぱ状の形状をしています。
一般的には外側の葉っぱがより大きく、内側の葉っぱがより小さくなります。

3. 対称性:

カーディオイド曲線は$ ( x ) $軸に対して対称です。
すなわち、$( \theta = 0 ) $および$ ( \theta = \pi ) $のときに曲線は$ ( x ) $軸と交わります。

4. 極限:

カーディオイド曲線は、極限$ ( a \rightarrow 0 ) $のときに原点に収束し、極限$ ( a \rightarrow \infty ) $のときに外側の葉っぱが無限遠方に広がります。

5. 応用:

カーディオイド曲線は数学的な興味の対象としてだけでなく、様々な応用があります。
例えば、物理学や工学の問題、またグラフィックデザインやアートなどの分野で使われることがあります。

カーディオイド曲線は、その美しい形状や数学的な特性から、多くの人々に愛される図形のひとつです。

ソースコード

Pythonでカーディオイド曲線を解いてグラフ化するコードは以下のようになります：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np
import matplotlib.pyplot as plt

# パラメータ
a = 1.0

# 角度の範囲
theta = np.linspace(0, 2 * np.pi, 1000)

# カーディオイド曲線の方程式
r = a * (1 - np.cos(theta))

# 極座標から直交座標系に変換
x = r * np.cos(theta)
y = r * np.sin(theta)

# グラフ描画
plt.plot(x, y)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Cardioid Curve')
plt.axis('equal')
plt.grid(True)
plt.show()

このコードは、カーディオイド曲線の方程式を解いて、極座標から直交座標系に変換し、結果をグラフ化します。

[実行結果]

ソースコード解説

以下にソースコードの詳細を解説します。

1. ライブラリのインポート:

  • numpyとmatplotlib.pyplotをインポートします。
    これらのライブラリは、数値計算やグラフ描画のために使用されます。

2. パラメータの設定:

  • aという名前の定数が$1.0$に設定されています。
    これはカーディオイド曲線の定数です。

3. 角度の範囲の生成:

  • np.linspace()関数を使用して、$0$から$(2\pi)$までの範囲を$1000$の等間隔で分割した角度の配列thetaを生成します。

4. カーディオイド曲線の方程式の計算:

  • カーディオイド曲線の極座標方程式$ ( r = a(1 - \cos(\theta)) ) $を使用して、各角度に対する距離$ (r) $を計算します。

5. 極座標から直交座標系への変換:

  • 極座標から直交座標系への変換を行います。
    これにより、各点の$(x)$座標と$(y)$座標が計算されます。

6. グラフの描画:

  • plt.plot()関数を使用して、直交座標系に変換された$(x)$と$(y)$の値をプロットします。
  • plt.xlabel()とplt.ylabel()を使用して、それぞれの軸にラベルを設定します。
  • plt.title()を使用して、グラフのタイトルを設定します。
  • plt.axis('equal')を使用して、軸のスケールを等しく設定します。
  • plt.grid(True)を使用して、グリッドを表示します。
  • plt.show()を使用して、グラフを表示します。

これにより、カーディオイド曲線が計算され、直交座標系に変換されてグラフ化されます。

グラフ解説

[実行結果]

このカーディオイド曲線のグラフは、極座標系で表される曲線を直交座標系に変換して描画したものです。

  • $X$軸と$Y$軸は直交座標系を表し、中心が原点になります。
  • カーディオイド曲線は、原点を中心とする座標系において、ある定数$ ( a ) $に対して極座標$ ( r ) $と角度$ ( \theta ) $の関係を表します。
  • グラフ上の曲線は、カーディオイド曲線の各点に対応し、$ ( x ) $軸と$ ( y ) $軸の値を持っています。
  • 曲線の形状は、原点を中心に放射状に伸びる葉っぱ状の形をしています。
  • カーディオイド曲線は、数学的に興味深い図形であり、心臓の形に似ていることから「カーディオイド（心臓状）」という名前がついています。

グラフには、原点を中心にしたカーディオイド曲線が描かれ、$X$軸と$Y$軸の目盛りが表示されています。

また、グリッドが表示され、各点の位置関係が視覚的に把握しやすくなっています。