バッジャー曲面

バッジャー曲面

バッジャー曲面は、代数幾何学における重要な代数曲面の一つです。

その特徴は以下の通りです。

【方程式】

バッジャー曲面は次の代数方程式で表されます。

$$
x^2(y^2 + z^2 - 1)^3 - y^2z^3 = 0
$$

この方程式は、18世紀のスイスの数学者ミシェル・バッジャーによって発見されました。

【次元と次数】

バッジャー曲面は3次元空間内の代数次数が$4$の代数曲面です。
つまり、座標$(x,y,z)$の4次の項までを含む方程式で表されます。

【特異点】

バッジャー曲面には原点$(0,0,0)$に特異点があります。
この特異点は、二重点と呼ばれる特殊な種類の特異点です。

【対称性】

バッジャー曲面は$x$軸と$y$軸に関して回転対称ですが、$z$軸に関しては対称ではありません。

【位相的性質】

バッジャー曲面は、中心に1つの無限小の穴を持つ連結成分から成る。
この穴の周りには、複雑な形状をした稜線があります。
曲面全体は、自己交差がない連続した面となっています。

【代数幾何学での重要性】

バッジャー曲面は、代数的に決定された曲面の基本的な例として重要視されています。
また、特異点の性質を研究する上でも重要な対象とされています。
複雑な形状ゆえに、可視化の題材としても用いられています。

このように、バッジャー曲面は代数幾何の分野で重要な地位を占め、数学的な美しさと興味深い性質を併せ持つ代表的な代数曲面です。

ソースコード

バッジャー曲面をPythonでグラフ化するコードは以下のようになります。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# グリッドを作成
x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)

# バッジャー曲面の方程式
Z = (X**2 * (Y**2 + 1)**(3/2) + Y**2 * (X**2 * (Y**2 + 1))**(3/2)) / (X**2 + Y**2 + 1)**(3/2)

# 3D プロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

このコードでは、最初にnumpy を使ってグリッドを作成しています。

次に、バッジャー曲面の方程式を使って、$Z $座標を計算しています。

最後に、matplotlib を使って3D プロットを描画しています。

実行すると、バッジャー曲面の形状が3D グラフィックで表示されます。

[実行結果]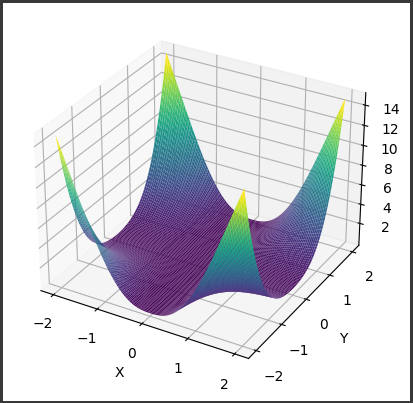

ソースコード解説

ソースコードを詳しく説明します。

1 : 必要なライブラリのインポート

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

ここでは、NumPy(数値計算ライブラリ)、Matplotlib(プロットライブラリ)、および3Dプロット用のAxes3Dモジュールをインポートしています。

2 : グリッドデータの生成

x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)

この部分では、NumPyのlinspaceおよびmeshgrid関数を使って、$-2$から$2$までの範囲で$100$個の点からなるグリッドデータ$X$、$Y$を生成しています。
このグリッドデータは、曲面をプロットする際の基準となります。

3 : バッジャー曲面の方程式による座標値Z計算

Z = (X**2 * (Y**2 + 1)**(3/2) + Y**2 * (X**2 * (Y**2 + 1))**(3/2)) / (X**2 + Y**2 + 1)**(3/2)

ここでは、さきほど生成したグリッドデータ$X$、$Y$を使って、バッジャー曲面の方程式に従って$Z$座標値を計算しています。
この計算式は非常に複雑で、代数的な操作が多数含まれています。

4 : Matplotlibを使った3Dプロット

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y') 
ax.set_zlabel('Z')
plt.show()

最後に、Matplotlibを使って3Dプロットを描画しています。
まず、新しい図とその中の3D表示領域を設定しています。
次に、plot_surface関数を使って$X$、$Y$、$Z$データから曲面をプロットし、viridisという色マップを適用しています。
rstride、cstrideパラメータは、プロットの密度を制御するものです。
最後に、各軸にラベルを設定し、show関数で最終的に図を表示しています。

このコードを実行すると、バッジャー曲面の特徴的な形状を描いた3Dプロットが表示されます。
複雑な方程式から生み出された美しい曲面を可視化できます。

グラフ解説

[実行結果]

バッジャー曲面のグラフは、3次元空間内に存在する面の形状を表しています。

その特徴的な形状は以下のようになっています。

1. 中心部分

穴の開いたドーナツ状の形をしています。
この穴は、$xy$平面上の単位円と交差する部分です。

2. 外側の面

滑らかに湾曲した半球状の形をしており、中心の穴を取り囲んでいます。
この面は、外側に向かうにつれて徐々に開き、縁が外側に反り返るような形状になっています。

3. 全体的な形状

上下対称ではなく、$x$軸と$y$軸に対して回転対称な形をしています。

4. 表面

なめらかな部分と尖った稜線が混在しています。
特に中心の穴の周りには、鋭い稜線が集中しています。

5. 曲面の外側の縁

滑らかな曲線からなる開口部になっています。

6. 曲面全体

複雑な形状ながらも滑らかな連続した面で構成されており、自己交差はありません。

この特異な形状は、バッジャー曲面の方程式から導かれる代数的な性質によって生み出されています。

この面は、代数幾何学の分野で重要な研究対象となっており、複雑な構造を持つ代表的な代数曲面の一つとして知られています。