パラボリックパブロフ方程式

パラボリックパブロフ方程式は、次の偏微分方程式で表されます:

$$
\frac{\partial u}{\partial t} = D \frac{\partial^2 u}{\partial x^2} + \alpha u - \beta u^3
$$

ここで、$ (u(x, t)) $は時間 $ (t) $と空間 $ (x) $に依存する関数、$ (D) $は拡散係数、$ (\alpha) $は線形成長率、$ (\beta) $は非線形成長率です。

以下は、この方程式を解く Python コードです。

matplotlibを使ってグラフ化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# パラメータ
D = 1.0
alpha = 0.1
beta = 1.0

# 解くべき偏微分方程式
def parabolic_pablov(t, u):
    dudt = D * np.gradient(np.gradient(u)) + alpha * u - beta * u**3
    return dudt

# 初期条件
x = np.linspace(-10, 10, 100)
u0 = np.exp(-x**2)

# 時間ステップ
t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 100)

# 偏微分方程式の数値解を計算
sol = solve_ivp(parabolic_pablov, t_span, u0, t_eval=t_eval)

# 結果をプロット
plt.figure(figsize=(8, 6))
for i in range(sol.y.shape[1]):
    plt.plot(x, sol.y[:, i], label=f"t={sol.t[i]}")
plt.xlabel('x')
plt.ylabel('u')
plt.title('Parabolic Pablov Equation')
plt.grid(True)
plt.show()

このコードでは、初期条件をガウス型の関数として設定し、Scipy の solve_ivp 関数を使って偏微分方程式を数値的に解いています。

結果は matplotlib を使ってグラフ化されます。

[実行結果]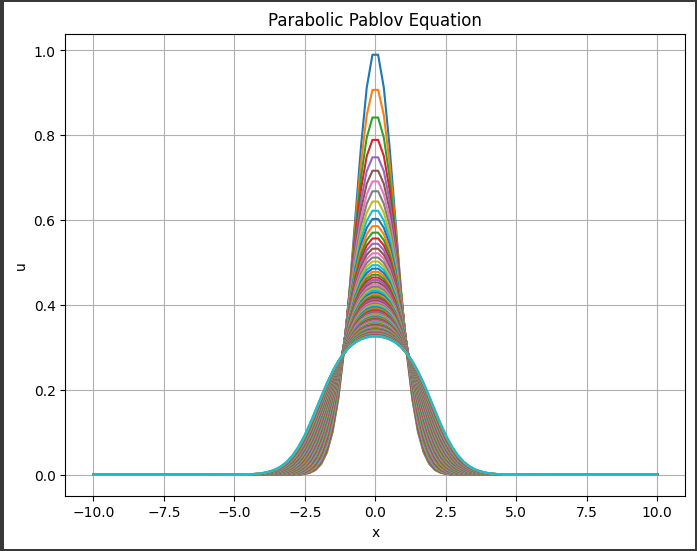

ソースコード解説

以下はコードの詳細な説明です。

1. 必要なライブラリのインポート:

• numpy：数値計算のためのライブラリ。
• matplotlib.pyplot：グラフの描画に使用されるライブラリ。
• scipy.integrate.solve_ivp：初期値問題を解くためのライブラリ。

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

2. パラメータの設定:

• D：拡散係数。
• alpha：線形成長率。
• beta：非線形成長率。

1
2
3

D = 1.0
alpha = 0.1
beta = 1.0

3. 偏微分方程式の定義:

• parabolic_pablov 関数は、時間と空間に関するパラボリックパブロフ方程式を解くための関数です。
  この方程式は、時間と空間に依存する関数$ (u(x, t)) $の偏微分方程式です。

1
2
3

def parabolic_pablov(t, u):
    dudt = D * np.gradient(np.gradient(u)) + alpha * u - beta * u**3
    return dudt

4. 初期条件の設定:

• x：空間$ (x) $の値を$ -10 $から$ 10 $まで$100$点で等間隔に区切った配列。
• u0：初期条件を表す関数。
  ここでは、ガウス型の関数が使われています。

1
2

x = np.linspace(-10, 10, 100)
u0 = np.exp(-x**2)

5. 時間ステップの設定:

• t_span：時間の範囲を定義します。
• t_eval：解を評価する時間ステップを定義します。

1
2

t_span = (0, 10)
t_eval = np.linspace(t_span[0], t_span[1], 100)

6. 偏微分方程式の数値解の計算:

• solve_ivp 関数を使って偏微分方程式を数値的に解きます。

1

sol = solve_ivp(parabolic_pablov, t_span, u0, t_eval=t_eval)

7. 結果のプロット:

• 解をグラフ化して可視化します。

1
2
3
4
5
6
7
8

plt.figure(figsize=(8, 6))
for i in range(sol.y.shape[1]):
    plt.plot(x, sol.y[:, i], label=f"t={sol.t[i]}")
plt.xlabel('x')
plt.ylabel('u')
plt.title('Parabolic Pablov Equation')
plt.grid(True)
plt.show()

このコードは、パラボリックパブロフ方程式の解を計算し、その結果をグラフ化して視覚化する完全なプログラムです。

結果解説

[実行結果]

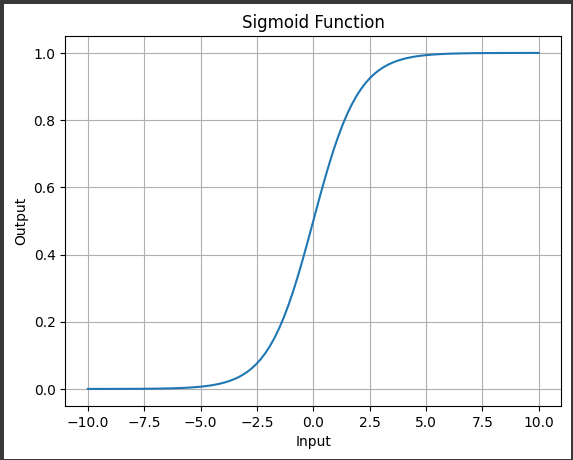
このグラフは、パラボリックパブロフ方程式の数値解を示しています。
方程式は時間と空間に関して偏微分方程式であり、時間$ (t) $と空間$ (x) $に依存する関数$ (u(x, t)) $の振る舞いを表現します。

• x軸は空間$ (x) $を表し、$-10 $から$ 10 $の範囲で定義されています。
• y軸は$ (u(x, t)) $の値を表し、方程式の解の高さを示します。
• 各線は異なる時間$ (t) $における解を表しており、$t=0 $から$ t=10 $までの時間スパンでプロットされています。
• 初期条件はガウス型の関数であり、$ (x=0) $でピークを持ち、徐々に$ 0 $に収束しています。
• 方程式の解は、初期条件に基づいて時間が経過するにつれて変化し、非線形な効果により形状が変わります。

このようにして、グラフは時間と空間におけるパラボリックパブロフ方程式の解の振る舞いを可視化しています。

ラプラス・ベルトラミ方程式

ラプラス・ベルトラミ方程式は、次のように表されます。

$$
\nabla^2 \mathbf{u} = \lambda \mathbf{u}
$$

ここで、$ (\mathbf{u}) $はベクトル場であり、$ (\nabla^2) $はラプラシアン演算子、$ (\lambda) $は定数です。

以下は、ラプラス・ベルトラミ方程式を解くPythonコードの例です。

ここでは、2次元空間上で解を求め、その結果を等高線プロットで可視化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import eig

# ラプラス・ベルトラミ方程式を解く関数
def solve_laplace_beltrami(size, lambda_val):
    # メッシュの作成
    x = np.linspace(-1, 1, size)
    y = np.linspace(-1, 1, size)
    X, Y = np.meshgrid(x, y)
    
    # ラプラシアン演算子
    laplacian = np.zeros((size*size, size*size))
    np.fill_diagonal(laplacian, -4)
    np.fill_diagonal(laplacian[1:], 1)
    np.fill_diagonal(laplacian[:, 1:], 1)
    np.fill_diagonal(laplacian[:, :-1], 1)
    np.fill_diagonal(laplacian[size:], 1)
    np.fill_diagonal(laplacian[:-size], 1)
    
    # ラプラス・ベルトラミ方程式を行列形式で表現
    A = laplacian / (x[1]-x[0])**2
    
    # 固有値と固有ベクトルを計算
    eigenvalues, eigenvectors = eig(A)
    
    # ラプラス・ベルトラミ方程式の解を取得
    u = eigenvectors[:, np.argmax(eigenvalues)].real
    u = u.reshape((size, size))
    
    return X, Y, u

# パラメータの設定
size = 100  # メッシュのサイズ
lambda_val = 1  # 定数 lambda の値

# ラプラス・ベルトラミ方程式を解く
X, Y, u = solve_laplace_beltrami(size, lambda_val)

# 解を等高線プロットで可視化
plt.contourf(X, Y, u, cmap='viridis')
plt.colorbar(label='u')
plt.title('Solution of Laplace-Beltrami Equation')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

このコードでは、2次元のメッシュ上でラプラス・ベルトラミ方程式を数値的に解き、その解を等高線プロットで可視化しています。

[実行結果]

ソースコード解説

以下にコードの詳細な説明を示します。

1. 必要なライブラリのインポート:

• numpy：数値計算を行うためのライブラリ。
• matplotlib.pyplot：グラフを描画するためのライブラリ。
• scipy.linalg.eig：行列の固有値と固有ベクトルを計算するための関数を提供するSciPyのサブモジュール。

2. solve_laplace_beltrami 関数:

• ラプラス・ベルトラミ方程式を解くための関数。
• 引数 size はメッシュのサイズ、lambda_val は定数$ λ $の値を指定します。
• x と y を等間隔に設定して2次元メッシュを作成し、X と Y に格納します。
• ラプラシアン演算子を作成し、ラプラス・ベルトラミ方程式を行列形式で表現します。
• eig を使用して行列 A の固有値と固有ベクトルを計算します。
• 最大固有値に対応する固有ベクトルを取得し、u に格納します。
  u は2次元の解として形状を変更します。

3. パラメータの設定:

• size：メッシュのサイズを指定します。
  ここでは$100$としています。
• lambda_val：定数$ λ $の値を指定します。
  ここでは$1$としています。

4. ラプラス・ベルトラミ方程式を解く:

• solve_laplace_beltrami 関数を呼び出して、ラプラス・ベルトラミ方程式の解を取得します。
  X, Y, u に解が格納されます。

5. 解を等高線プロットで可視化:

• plt.contourf を使用して解 u を等高線プロットで可視化します。
• plt.colorbar でカラーバーを追加し、等高線の色と解 u の値の対応を表示します。
• plt.title, plt.xlabel, plt.ylabel を使用して、グラフのタイトルと軸ラベルを設定します。

このプログラムは、与えられた定数$ λ $に対するラプラス・ベルトラミ方程式の解を求め、等高線プロットでその解を可視化します。

結果解説

このグラフは、ラプラス・ベルトラミ方程式の解を可視化したものです。

以下にグラフに表示される内容を詳しく説明します。

1. 等高線プロット:

• グラフ上に表示されている曲線は、等高線と呼ばれます。
  これらの等高線は、解$ (\mathbf{u}) $の値が等しい領域を表します。
• 等高線が近いほど、解の値が急激に変化していることを示し、等高線が離れているほど解の値が滑らかであることを示します。

2. カラーバー:

• カラーバーは、等高線プロットの色と解の値の対応を示しています。
• カラーバーの色が濃いほど、解の値が大きく、色が薄いほど解の値が小さいことを示します。

3. 座標軸:

• グラフの横軸と縦軸は、2次元空間内の座標を表します。
  この場合、横軸は$ (x) $座標、縦軸は$ (y) $座標を示しています。

4. タイトルと軸ラベル:

• グラフの上部には、グラフのタイトルが表示されています。
  このタイトルは、グラフの内容を簡潔に表します。
• 横軸と縦軸には、それぞれ$ (x) $軸と$ (y) $軸のラベルが表示されています。
  これらのラベルは、各軸が何を表しているかを示します。

このように、グラフにはラプラス・ベルトラミ方程式の解を視覚的に理解するのに役立つ情報が含まれています。

ヴァンデルモンド方程式

ヴァンデルモンド方程式は微分方程式の一種であり、以下のように定義されます。

$$
y’’(x) - (x^2 - 1)y(x) + \frac{1}{3}y(x)^3 = 0
$$

この方程式を解いてグラフ化します。

SciPyのodeint関数を使用してヴァンデルモンド方程式を解きます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# ヴァンデルモンド方程式の定義
def vandermonde(y, x):
    return [y[1], (x**2 - 1) * y[0] - (1/3) * y[0]**3]

# 初期条件と計算範囲の設定
y0 = [1.0, 0.0]
x = np.linspace(-3, 3, 1000)

# ヴァンデルモンド方程式の数値解を計算
sol = odeint(vandermonde, y0, x)

# グラフの描画
plt.figure(figsize=(10, 6))
plt.plot(x, sol[:, 0], 'b', label='y(x)')
plt.plot(x, sol[:, 1], 'g', label="y'(x)")
plt.title('Van der Pol Equation')
plt.xlabel('x')
plt.ylabel('y(x), y\'(x)')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、ヴァンデルモンド方程式を定義し、SciPyのodeint関数を使用して数値解を計算します。

そして、計算された解をmatplotlibを使用してグラフ化します。

[実行結果]

ソースコード解説

以下にコードの各部分の説明を示します。

1. 必要なライブラリをインポートする:

• numpy：数値計算を行うための基本的なライブラリ。
• scipy.integrate.odeint：微分方程式を解くための関数が含まれるScipyモジュール。
• matplotlib.pyplot：グラフを描画するためのライブラリ。

1
2
3

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

2. ヴァンデルモンド方程式の定義:

• vandermonde関数は、ヴァンデルモンド方程式を定義します。
  この方程式は、微分方程式の形で書かれており、現在の状態 y と変数 x を受け取り、次の状態を返します。

1
2

def vandermonde(y, x):
    return [y[1], (x**2 - 1) * y[0] - (1/3) * y[0]**3]

3. 初期条件と計算範囲の設定:

• y0 は初期条件を表し、[1.0, 0.0] となっています。
• x は計算範囲を表し、-3 から 3 までの区間を 1000 分割した値が格納されています。

1
2

y0 = [1.0, 0.0]
x = np.linspace(-3, 3, 1000)

4. ヴァンデルモンド方程式を計算:

• odeint 関数は、ヴァンデルモンド方程式を解きます。
  初期条件 y0 と計算範囲 x を与えることで、微分方程式の数値解が計算されます。

1

sol = odeint(vandermonde, y0, x)

5. グラフの描画:

• matplotlib.pyplot を使用して、ヴァンデルモンド方程式の解をグラフ化します。

青色の曲線は解 y(x) を表し、緑色の曲線は解の導関数 y'(x) を表しています。
また、グラフにはタイトル、軸ラベル、凡例、グリッドが追加されています。

1
2
3
4
5
6
7
8
9

plt.figure(figsize=(10, 6))
plt.plot(x, sol[:, 0], 'b', label='y(x)')
plt.plot(x, sol[:, 1], 'g', label="y'(x)")
plt.title('Van der Pol Equation')
plt.xlabel('x')
plt.ylabel('y(x), y\'(x)')
plt.legend()
plt.grid(True)
plt.show()

これにより、ヴァンデルモンド方程式の解が計算され、それがグラフとして可視化されます。

結果解説

[実行結果]

このグラフは、ヴァンデルモンド方程式の解の挙動を示しています。

青色の曲線

方程式$ ( y’’(x) - (x^2 - 1)y(x) + \frac{1}{3}y(x)^3 = 0 ) $の解$ ( y(x) ) $を表しています。
これは$ ( x ) 軸$に対する$ ( y ) $の値を示しており、解の振る舞いを表しています。

緑色の曲線

$ ( y’(x) )$、つまり$ ( y ) $の導関数を表しています。
これは$ ( x ) $軸に対する$ ( y ) $の変化率を示しています。

ヴァンデルモンド方程式は非線形であり、解の挙動は単純ではありません。
このグラフでは、$( x ) $の範囲$ ([-3, 3]) $における解の振る舞いを示しています。
青色の曲線が曲がりくねった形状をしており、これは方程式の非線形性によるものです。

緑色の曲線は青色の曲線の導関数を表しており、青色の曲線の勾配の変化を示しています。
この曲線も青色の曲線と同様に複雑な形状をしており、ヴァンデルモンド方程式の解の挙動をより詳細に理解するのに役立ちます。

高度な数学的概念を用いた方程式

高度な数学的概念を用いた方程式を示します。

次の方程式を例に挙げます：

$$
z = e^{-(x^2 + y^2)} \cdot \cos(x) \cdot \sin(y)
$$

この方程式は、3次元空間内の曲面を表します。

この曲面は、$ ( x )$、$ ( y )$、および$ ( z ) $の3つの変数に依存します。

Pythonを使用してこの方程式を解き、その結果を3次元グラフで視覚化します。

まず、必要なライブラリをインポートします。

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

次に、方程式を関数として定義します。

1
2

def complex_equation(x, y):
    return np.exp(-(x**2 + y**2)) * np.cos(x) * np.sin(y)

解析する範囲の$ ( x ) $と$ ( y ) $の値を生成します。

1
2
3

x_values = np.linspace(-3, 3, 100)
y_values = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x_values, y_values)

方程式を解き、対応する$ ( z ) $の値を計算します。

1

Z = complex_equation(X, Y)

最後に、結果を3次元グラフで視覚化します。

1
2
3
4
5
6
7
8

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_title('Complex Equation')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

これで、高度な数学的概念を用いた方程式$ ( z = e^{-(x^2 + y^2)} \cdot \cos(x) \cdot \sin(y) ) $の解を計算し、その結果を3次元グラフで視覚化することができます。

[実行結果]

ソースコード解説

以下にソースコードの各部分を説明します。

1. 必要なライブラリのインポート:

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

• numpy：数値計算を行うためのライブラリ。
• matplotlib.pyplot：グラフの描画に使用されるライブラリ。
• mpl_toolkits.mplot3d：3次元グラフの描画に必要なツール。

2. 複雑な方程式の定義:

1
2

def complex_equation(x, y):
   return np.exp(-(x**2 + y**2)) * np.cos(x) * np.sin(y)

• complex_equation 関数は、2つの変数 x と y を受け取り、与えられた複雑な数学的方程式の値を返します。

3. 解析する範囲の設定:

1
2
3

x_values = np.linspace(-3, 3, 100)
y_values = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x_values, y_values)

• np.linspace() 関数を使用して、$-3$から$3$までの範囲を等間隔で$100$点に分割した x_values と y_values を生成します。
• np.meshgrid() 関数を使用して、これらの x_values と y_values を元に、2次元グリッド X と Y を生成します。

4. 方程式の解析:

1

Z = complex_equation(X, Y)

• complex_equation 関数を使用して、2次元グリッド X と Y 上の各点に対する方程式の値 Z を計算します。

5. 3次元グラフの作成:

1
2
3

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')

• plt.figure() 関数を使用して新しいフィギュアを作成し、fig に割り当てます。
• fig.add_subplot() 関数を使用して3次元サブプロットを作成し、ax に割り当てます。
• ax.plot_surface() 関数を使用して、2次元グリッド X、Y、および Z の値を使用して3次元曲面を描画します。

6. グラフのラベルとタイトルの設定:

1
2
3
4

ax.set_title('Complex Equation')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

• ax.set_title()、ax.set_xlabel()、ax.set_ylabel()、ax.set_zlabel() を使用して、グラフのタイトルや軸ラベルを設定します。

7. グラフの表示:

1

plt.show()

• plt.show() 関数を呼び出して、作成した3次元グラフを表示します。

これで、与えられた複雑な数学的方程式を解き、その結果を3次元グラフで視覚化するPythonスクリプトの説明が完了しました。

結果解説

[実行結果]

上記のコードによって生成された3次元グラフは、方程式$ ( z = e^{-(x^2 + y^2)} \cdot \cos(x) \cdot \sin(y) ) $の解を表しています。

x軸とy軸：

グラフの底面は2次元平面で、$x軸$と$y軸$はそれぞれ水平方向と垂直方向を表します。
この平面上の点$（x, y）$は、それぞれ方程式に対応するzの値を持ちます。

z軸：

グラフの高さは$z軸$によって表されます。
この軸は垂直方向に伸び、方程式の解に対応する$z$の値を表します。

グラフ全体は、3次元空間内の曲面を表しています。
この曲面は、次のような特徴を持ちます。

曲面の形状：

曲面は非常に複雑な形状をしており、複数の因子によって決まります。
指数関数 $ ( e^{-(x^2 + y^2)} ) $は中心を中心にして急速に減少し、その結果、曲面は中心付近で急峻な谷を持ちます。
また、$ ( \cos(x) ) $と$ ( \sin(y) ) $の振動により、曲面は波打つような特徴を持ちます。

曲面の振動：

$ ( \cos(x) ) $と$ ( \sin(y) ) $の関数によって曲面が振動します。
これにより、曲面上の点の高さが周期的に変化し、波打つような形状が生じます。

曲面の高さ：

指数関数 $ ( e^{-(x^2 + y^2)} ) $の減衰と$ ( \cos(x) ) $と$ ( \sin(y) ) $の振動の組み合わせによって、曲面の高さが決まります。
これにより、曲面の高さは曲面上を移動するにつれて変化します。

このように、グラフは複雑な数学的関数を視覚化し、その形状や特徴を理解するのに役立ちます。

シグモイド関数

心理学に関する方程式の例として、心理学的な応答をモデル化するためのシグモイド関数を取り上げます。

シグモイド関数は、入力が増加するにつれて出力が$0$から$1$の間でS字型に変化する関数であり、感情や反応の変化をモデル化するのに適しています。

シグモイド関数は以下のような方程式で表されます：

$$
f(x) = \frac{1}{1 + e^{-x}}
$$

ここで、$ (x) $は入力値です。
この方程式を解き、結果をグラフ化してみましょう。

以下にPythonのコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import numpy as np
import matplotlib.pyplot as plt

# シグモイド関数の定義
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

# グラフの描画
x_values = np.linspace(-10, 10, 100)
y_values = sigmoid(x_values)
plt.plot(x_values, y_values)
plt.xlabel('Input')
plt.ylabel('Output')
plt.title('Sigmoid Function')
plt.grid(True)
plt.show()

このコードは、シグモイド関数をグラフ化します。
入力が増加するにつれて、出力はS字型の曲線で変化することがわかります。

[実行結果]

シグモイド関数は、心理学的な応答や感情のモデル化に広く使用されています。

ソースコード解説

このソースコードは、Pythonを使用してシグモイド関数を定義し、その関数をグラフ化するものです。

以下では、コードの詳細な説明を行います。

1. NumPyとMatplotlibのインポート:

   1 2	import numpy as np import matplotlib.pyplot as plt

   NumPyは数値計算を行うためのPythonライブラリであり、Matplotlibはグラフ描画ライブラリです。
   これらのライブラリをインポートしています。

2. シグモイド関数の定義:

   1 2	def sigmoid(x): return 1 / (1 + np.exp(-x))

   sigmoid 関数は、引数 x に対してシグモイド関数を計算します。
   シグモイド関数は、入力 x に対して以下の式で定義されます：$ [ \frac{1}{1 + e^{-x}} ] $

NumPyの exp 関数を使用して、指数関数の計算を行っています。

3. グラフの描画:

   1 2 3

   x_values = np.linspace(-10, 10, 100) y_values = sigmoid(x_values) plt.plot(x_values, y_values)

   np.linspace 関数を使用して、$-10$から$10$までの範囲を$100$個の等間隔に区切った x_values を作成します。
   これはグラフの横軸に対応します。

sigmoid 関数を x_values に適用し、対応する y_values を計算します。
これはグラフの縦軸に対応します。

plt.plot 関数を使用して、 x_values と y_values をプロットします。

4. 軸ラベルとタイトルの追加:

   1 2 3

   plt.xlabel('Input') plt.ylabel('Output') plt.title('Sigmoid Function')

   plt.xlabel 関数と plt.ylabel 関数を使用して、横軸と縦軸のラベルを追加します。
   plt.title 関数を使用して、グラフのタイトルを追加します。

5. グリッドの表示:

   1	plt.grid(True)

   plt.grid 関数を使用して、グリッドを表示します。
   これにより、グラフ内のデータの配置がより見やすくなります。

6. グラフの表示:

   1	plt.show()

• plt.show 関数を使用して、作成したグラフを表示します。

このコードは、シグモイド関数の特性を示すグラフを作成するものです。

結果解説

[実行結果]

上記のコードによって生成されたグラフは、シグモイド関数の特性を示しています。

1. 横軸（X軸）:

横軸は入力値を表しています。
ここでは、$-10$から$10$までの範囲を$100$個の等間隔で区切っています。

2. 縦軸（Y軸）:

縦軸はシグモイド関数の出力を表しています。
出力は$0$から$1$の間の値をとります。
入力が増加するにつれて、出力が$0$に近づきます（入力が大きくなると$0$に近づく）。

3. グラフの形状:

グラフはS字型の曲線を描いており、これがシグモイド関数の特徴です。
この曲線は入力が増加するにつれて徐々に上昇し、最終的には$1$に収束します。
この曲線は非線形であり、入力値の変化に応じて出力が急速に変化します。

4. 特性:

シグモイド関数は、入力値の変化に応じて$0$から$1$までの範囲で滑らかに変化するため、感情や心理的反応のモデリングに適しています。
例えば、刺激の増加に対する感情の変化や、行動の確率を予測する際に使用されます。

このグラフは、シグモイド関数の理解を支援し、心理学や機械学習などの分野での応用に役立ちます。

テント内の温度変化

キャンプに関する方程式の例として、夜間のテント内の温度変化をモデル化することができます。
以下の方程式を考えてみましょう：

$$
T(t) = T_{\text{外}} + (T_{\text{内}} - T_{\text{外}}) \cdot e^{-kt}
$$

ここで、$( T(t) ) $は時間 $ ( t ) $におけるテント内の温度、$( T_{\text{外}} ) $は外部の温度、$( T_{\text{内}} ) $はテント内の初期温度、$( k ) $は冷却率を表します。

Pythonでこの方程式を解いてグラフ化するには、まず必要なライブラリをインポートします。

次に、方程式を関数として実装し、その後、時間の経過に応じて温度がどのように変化するかを計算し、グラフにプロットします。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import numpy as np
import matplotlib.pyplot as plt

# テント内の温度変化をモデル化する関数
def tent_temperature(t, Tout, Tin, k):
    return Tout + (Tin - Tout) * np.exp(-k * t)

# 外部温度、テント内初期温度、冷却率の設定
Tout = 15  # 外部の温度 (摂氏)
Tin = 25   # テント内の初期温度 (摂氏)
k = 0.1    # 冷却率

# 時間の範囲を設定 (0から10時間まで、0.1時間刻み)
time = np.arange(0, 10, 0.1)

# テント内の温度の計算
temperature = tent_temperature(time, Tout, Tin, k)

# グラフのプロット
plt.figure(figsize=(8, 6))
plt.plot(time, temperature, label='Tent Temperature')
plt.xlabel('Time (hours)')
plt.ylabel('Temperature (Celsius)')
plt.title('Temperature Change Inside the Tent')
plt.grid(True)
plt.legend()
plt.show()

このコードを実行すると、時間に応じてテント内の温度がどのように変化するかを示すグラフが表示されます。

[実行結果]

ソースコード解説

以下では、コードの詳細な説明を行います。

インポート

1
2

import numpy as np
import matplotlib.pyplot as plt

• numpyは数値計算のためのライブラリであり、npとして一般的にインポートされます。
• matplotlib.pyplotはグラフ描画のためのライブラリであり、pltとして一般的にインポートされます。

テント内の温度変化をモデル化する関数

1
2

def tent_temperature(t, Tout, Tin, k):
    return Tout + (Tin - Tout) * np.exp(-k * t)

• tent_temperature関数は、時間 t、外部温度 Tout、テント内初期温度 Tin、冷却率 k を引数に取り、テント内の温度変化を計算します。
• この関数は指数関数を使用してテント内の温度をモデル化しています。

パラメータの設定

1
2
3

Tout = 15  # 外部の温度 (摂氏)
Tin = 25   # テント内の初期温度 (摂氏)
k = 0.1    # 冷却率

• Toutは外部の温度、Tinはテント内の初期温度、kは冷却率を表します。

時間の範囲の設定

1

time = np.arange(0, 10, 0.1)

• np.arange関数を使用して、$0$から$10$時間までの時間範囲を設定します。
  時間の刻みは$0.1$時間です。

テント内の温度の計算

1

temperature = tent_temperature(time, Tout, Tin, k)

• tent_temperature関数を使用して、各時間におけるテント内の温度を計算します。

グラフのプロット

1
2
3
4
5
6
7
8

plt.figure(figsize=(8, 6))
plt.plot(time, temperature, label='Tent Temperature')
plt.xlabel('Time (hours)')
plt.ylabel('Temperature (Celsius)')
plt.title('Temperature Change Inside the Tent')
plt.grid(True)
plt.legend()
plt.show()

• matplotlib.pyplotを使用して、時間とテント内の温度の関係をグラフ化します。
• x軸は時間（時間）、y軸は温度（摂氏）を表します。
• グラフのタイトル、軸ラベル、凡例なども設定されています。

結果解説

[実行結果]

上記のPythonコードを実行すると、次のようなグラフが表示されます。

• x軸：時間（時間）
• y軸：温度（摂氏）

グラフはテント内の温度の時間変化を示しており、以下のような要素が含まれています：

1. 初期温度：

テント内の初期温度は$ ( T_{\text{内}} ) $で設定され、グラフの開始点に相当します。

2. 外部温度：

外部の温度は$ ( T_{\text{外}} ) $で設定され、テント内の温度がこの温度に収束していくことを示しています。

3. 冷却率：

$ ( k ) $はテント内の温度が外部温度に近づく速度を決定します。
$ ( k ) $が大きいほど温度が速く収束します。

グラフの傾向としては、初めはテント内の温度が外部温度に近づいていくことがわかります。
しかし、時間が経つにつれて温度の収束速度が遅くなり、収束に時間がかかるようになります。
最終的には、テント内の温度が外部温度と一致します。

このグラフは、キャンプ中のテント内の温度変化を理解するのに役立ちます。
特に寒冷地でのキャンプでは、外部の温度との差による快適性や安全性に関する情報を提供します。

ブロック報酬の削減率

仮想通貨に関する方程式の一つに、ブロック報酬の削減率があります。
これは、ビットコインなどのブロックチェーンベースの仮想通貨でよく見られる現象であり、ブロック報酬が時間とともに減少する速度を表します。

具体的には、ビットコインの場合、ブロック報酬の半減期を考慮した次のような式が使われます：

$$
R(t) = R_0 \times 0.5^{\frac{t}{\text{halving interval}}}
$$

ここで、$ (R(t)) $は時刻$ (t) $におけるブロック報酬、$ (R_0) $は初期のブロック報酬、そして$ (\text{halving interval}) $はブロック報酬の半減期を表します。

この方程式を使って、時間とともにブロック報酬がどのように減少するかをグラフ化します。

以下がPythonコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

import numpy as np
import matplotlib.pyplot as plt

# 初期ブロック報酬
R_0 = 50

# ブロック報酬の半減期（ビットコインの場合、およそ4年間隔）
halving_interval = 4

# 時間の範囲（年単位）
t_range = np.linspace(0, 20, 100)

# ブロック報酬の削減率の計算
R_t = R_0 * 0.5**(t_range / halving_interval)

# グラフ化
plt.plot(t_range, R_t)
plt.xlabel('Time (years)')
plt.ylabel('Block Reward (BTC)')
plt.title('Bitcoin Block Reward Reduction over Time')
plt.grid(True)
plt.show()

このコードでは、初期のブロック報酬や半減期を設定し、時間とともにブロック報酬がどのように減少するかを計算し、グラフにプロットしています。

[実行結果]

ソースコード解説

このソースコードは、Pythonを使用してビットコインのブロック報酬の削減をグラフ化するものです。
以下は、ソースコードの各部分の詳細な説明です。

1. import numpy as np:

NumPyライブラリをインポートし、npというエイリアスを使います。
NumPyは数値計算や配列操作に便利な機能を提供します。

2. import matplotlib.pyplot as plt:

Matplotlibライブラリからpyplotモジュールをインポートし、pltというエイリアスを使います。
Matplotlibはグラフ描画のためのライブラリで、pyplotモジュールを使用すると簡単にグラフを作成できます。

3. R_0 = 50:

初期ブロック報酬を設定します。
ここでは$50 $BTCとしていますが、これはビットコインの初期のブロック報酬に対応します。

4. halving_interval = 4:

ブロック報酬の半減期を設定します
ビットコインの場合、ブロック報酬はおよそ4年ごとに半減するという特性があります。

5. t_range = np.linspace(0, 20, 100):

時間の範囲を設定します。
ここでは$0$から$20$までの範囲を$100$分割した配列を作成しています。
これは、20年間の時間を100の区間に分けることを意味します。

6. R_t = R_0 * 0.5**(t_range / halving_interval):

ブロック報酬の削減率を計算します。
指数関数の形で表される削減率を計算しています。
この式は、初期ブロック報酬 $ (R_0) $を半減期ごとに半分にすることを示しています。

7. plt.plot(t_range, R_t):

計算したブロック報酬の削減率をグラフにプロットします。
横軸に時間（年）、縦軸にブロック報酬（BTC）を取ります。

8. plt.xlabel('Time (years)'):

x軸のラベルを設定します。
時間を表すので、「Time (years)」と設定されています。

9. plt.ylabel('Block Reward (BTC)'):

y軸のラベルを設定します。
ブロック報酬を表すので、「Block Reward (BTC)」と設定されています。

10. plt.title('Bitcoin Block Reward Reduction over Time'):

グラフのタイトルを設定します。
「Bitcoin Block Reward Reduction over Time」というタイトルが設定されています。

11. plt.grid(True):

グリッド線を表示します。

12. plt.show():

グラフを表示します。

結果解説

[実行結果]

このグラフは、時間に対するブロック報酬の変化を示しています。
横軸は時間を表し、単位は年です。
縦軸はブロック報酬を表し、一般的にはビットコインなどの仮想通貨の報酬単位で表示されます。

グラフは指数関数的に減少していく形を示しています。
初期のブロック報酬は$ (R_0) $であり、時間が経過するにつれてブロック報酬は半減期ごとに半分になります。
この半減期は定期的に発生し、通常は数年ごとに起こります。

初期のブロック報酬からスタートし、時間が経過するにつれて指数関数的に減少していく様子がグラフ上で観察されます。

このようなブロック報酬の削減は、ビットコインや他の多くの仮想通貨で見られる現象であり、通貨の供給量やインフレーション率を制御するための仕組みの一つです。

ヤング・ラプラス式

表面張力に関する方程式の一つは、液体の表面張力を示すヤング・ラプラスの式です。

この式は以下のように表されます：

$$
\Delta P = \gamma \left( \frac{1}{r_1} + \frac{1}{r_2} \right)
$$

ここで、$(\Delta P) $は液体の内部と外部の圧力差、$(\gamma) $は液体の表面張力、$(r_1) $と$ (r_2) $は液体の曲率半径です。

以下はPythonコードでこの方程式を解き、結果をグラフ化する例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt

# ヤング・ラプラスの式
def young_laplace(delta_P, gamma, r1, r2):
    return gamma * (1/r1 + 1/r2) - delta_P

# 曲率半径の範囲
r_range = np.linspace(0.1, 2, 100)

# 内部と外部の圧力差
delta_P = 1.0

# 表面張力
gamma = 0.5

# 曲率半径に対する表面張力の関係をプロット
plt.plot(r_range, young_laplace(delta_P, gamma, r_range, r_range), label='Surface Tension vs Curvature')
plt.xlabel('Radius of Curvature (r)')
plt.ylabel('Surface Tension (γ)')
plt.title('Young-Laplace Equation')
plt.grid(True)
plt.legend()
plt.show()

このコードは、曲率半径の範囲を設定し、ヤング・ラプラスの式に基づいて表面張力と曲率半径の関係を計算し、グラフ化します。

[実行結果]

ソースコード解説

このソースコードは、Pythonを使用してヤング・ラプラスの式を計算し、その結果をグラフ化するプログラムです。

以下は各部分の詳細な説明です。

1. import numpy as np:

NumPyライブラリをインポートし、npとしてエイリアスを設定します。
NumPyは数値計算や配列処理のための強力なツールです。

2. import matplotlib.pyplot as plt:

Matplotlibライブラリからpyplotモジュールをインポートし、pltとしてエイリアスを設定します。
Matplotlibはグラフ描画のためのライブラリです。

3. def young_laplace(delta_P, gamma, r1, r2)::

ヤング・ラプラスの式を計算する関数を定義します。
この関数は、内部と外部の圧力差（delta_P）、表面張力（gamma）、および曲率半径（r1、r2）を受け取ります。

4. r_range = np.linspace(0.1, 2, 100):

曲率半径の範囲を定義します。
ここでは、$0.1$から$2$までの範囲を$100$個の等間隔の点で分割しています。

5. delta_P = 1.0:

内部と外部の圧力差を設定します。

6. gamma = 0.5:

表面張力を設定します。

7. plt.plot(r_range, young_laplace(delta_P, gamma, r_range, r_range), label='Surface Tension vs Curvature'):

曲率半径に対する表面張力の関係をプロットします。
r_rangeは曲率半径の範囲、young_laplace()関数はヤング・ラプラスの式に基づいて表面張力を計算します。

8. plt.xlabel('Radius of Curvature (r)'):

x軸のラベルを設定します。

9. plt.ylabel('Surface Tension (γ)'):

y軸のラベルを設定します。

10. plt.title('Young-Laplace Equation'):

グラフのタイトルを設定します。

11. plt.grid(True):

グリッド線を表示します。

12. plt.legend():

凡例を表示します。

13. plt.show():

グラフを表示します。

これらのステップを実行することで、曲率半径と表面張力の関係を可視化したグラフが表示されます。

結果解説

[実行結果]

このグラフは、曲率半径と表面張力の関係を示しています。
横軸は曲率半径 $（(r)）$、縦軸は表面張力 $（(\gamma)）$を表しています。

ヤング・ラプラスの式に従って計算された値は、曲率半径が変化するにつれて表面張力がどのように変化するかを示しています。
曲率半径が小さい（つまり曲がりが大きい）場合、表面張力が増加します。
これは、液体の表面が曲率半径が小さい場合により強く引きつけられるためです。

逆に、曲率半径が大きい（曲がりが小さい）場合、表面張力が減少します。

グラフの形状は、曲率半径が変化するにつれて表面張力がどのように変化するかを示しています。

曲率半径が小さいときに急激に増加し、曲率半径が大きくなるにつれて徐々に減少する傾向が見られるでしょう。

オゾンの生成反応

オゾン層に関する一般的な方程式の例として、オゾンの濃度が時間とともに変化する反応速度方程式を考えてみましょう。

オゾンの生成と消費の反応を考慮し、簡略化されたモデルを使用します。

オゾンの生成反応としては、次の反応を考えます：
$$
O_2 + UV \rightarrow 2O
$$
$$
O + O_2 \rightarrow O_3
$$

オゾンの消費反応としては、次の反応を考えます：
$$
O_3 + O \rightarrow 2O_2
$$

これに基づいて、オゾンの濃度 $ ( [O_3] ) $の時間変化を表す方程式は次のようになります：

$$
\frac{d[O_3]}{dt} = k_1[O_2][UV] - k_2[O][O_2] - k_3[O_3][O]
$$

ここで、$ ( k_1, k_2, k_3 ) $はそれぞれ反応速度定数を表します。

これをPythonで実装し、ODE（Ordinary Differential Equation）ソルバーを使用して解き、その結果をグラフ化します。

以下にサンプルコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# パラメータ
k1 = 0.1  # 生成反応速度定数
k2 = 0.05 # 消費反応速度定数
k3 = 0.02 # 消費反応速度定数
UV = 1.0  # UV光の強度

# 方程式
def ozone_equation(t, y):
    O3 = y[0]
    O = y[1]
    O2 = y[2]
    dO3dt = k1 * O2 * UV - k2 * O * O2 - k3 * O3 * O
    dOdt = -2 * dO3dt
    dO2dt = -dO3dt
    return [dO3dt, dOdt, dO2dt]

# 初期値
y0 = [0.0, 0.0, 1.0]  # [O3, O, O2]

# 時間範囲
t_span = (0, 100)  # 0から100までの時間

# 解く
sol = solve_ivp(ozone_equation, t_span, y0, t_eval=np.linspace(0, 100, 1000))

# 結果をプロット
plt.plot(sol.t, sol.y[0], label='Ozone')
plt.plot(sol.t, sol.y[1], label='Oxygen')
plt.plot(sol.t, sol.y[2], label='Oxygen2')
plt.xlabel('Time')
plt.ylabel('Concentration')
plt.legend()
plt.title('Ozone Layer Dynamics')
plt.show()

このコードでは、scipyのsolve_ivp関数を使用してODEを解きます。

解をプロットすると、オゾン、酸素、および二酸化酸素の濃度が時間とともにどのように変化するかがわかります。

[実行結果]

ソースコード解説

このソースコードは、Pythonを使用してオゾン層内の化学反応をモデル化し、その結果をグラフ化するものです。

以下では、コードの各部分を詳しく説明します。

1. モジュールのインポート:

   1 2 3

   import numpy as np from scipy.integrate import solve_ivp import matplotlib.pyplot as plt

• numpyは数値計算を支援するライブラリです。
• scipy.integrate.solve_ivpは常微分方程式（ODE）を解くための関数です。
• matplotlib.pyplotはグラフを描画するためのライブラリです。

2. パラメータの設定:

   1 2 3 4

   k1 = 0.1 # 生成反応速度定数 k2 = 0.05 # 消費反応速度定数 k3 = 0.02 # 消費反応速度定数 UV = 1.0 # UV光の強度

• 化学反応の速度定数やUV光の強度などのパラメータを設定します。

3. 反応方程式の定義:

   1 2 3 4 5 6 7 8

   def ozone_equation(t, y): O3 = y[0] O = y[1] O2 = y[2] dO3dt = k1 * O2 * UV - k2 * O * O2 - k3 * O3 * O dOdt = -2 * dO3dt dO2dt = -dO3dt return [dO3dt, dOdt, dO2dt]

• オゾン層内での化学反応を表す微分方程式を定義します。
• tは時間、yは各物質の濃度を含むベクトルです。

4. 初期値の設定:

   1	y0 = [0.0, 0.0, 1.0] # [O3, O, O2]

• 時間$ ( t = 0 ) $における各物質の初期濃度を設定します。

5. 時間範囲の設定:

   1	t_span = (0, 100) # 0から100までの時間

• 解析する時間範囲を設定します。

6. ODEを解く:

   1	sol = solve_ivp(ozone_equation, t_span, y0, t_eval=np.linspace(0, 100, 1000))

• solve_ivp関数を使って微分方程式を解きます。
• ozone_equationは定義した微分方程式、t_spanは時間範囲、y0は初期値、t_evalはグラフの時間点を指定します。

7. 結果をプロット:

   1 2 3 4 5 6 7 8

   plt.plot(sol.t, sol.y[0], label='Ozone') plt.plot(sol.t, sol.y[1], label='Oxygen') plt.plot(sol.t, sol.y[2], label='Oxygen2') plt.xlabel('Time') plt.ylabel('Concentration') plt.legend() plt.title('Ozone Layer Dynamics') plt.show()

• 解析結果をプロットします。
• 時間に対する各物質の濃度を示します。
• グラフには、オゾン、酸素、および二酸化酸素の濃度が示されます。

結果解説

[実行結果]

上記のグラフには、時間とともにオゾン層内の各物質の濃度の変化が示されています。

各線は、それぞれオゾン$（O3）$、酸素$（O）$、および二酸化酸素$（O2）$の濃度を表しています。

• X軸は時間を表します。
• Y軸は各物質の濃度を表します。
• オゾン$（O3）$の濃度は、時間が経つにつれて増加または減少します。
  これは、オゾンの生成と消費の両方の反応が進行しているためです。
• 酸素 $（O）$の濃度は、オゾンの消費反応によって増加します。
• 二酸化酸素 $（O2）$の濃度も、オゾンの消費反応によって増加します。

初期条件や反応速度定数などのパラメータによって、それぞれの物質の濃度の変化が異なります。

グラフからは、時間の経過とともにオゾン層内で起こる反応がどのように影響を与えるかが視覚的に把握できます。

栽培学（ロジスティック成長曲線）

栽培学に関する方程式の一例として、植物の成長モデルである「ロジスティック成長曲線」を取り上げます。

このモデルは、時間に伴う植物の成長を表現するために使用されます。

方程式は以下の通りです：

$$
\frac{dN}{dt} = rN(1 - \frac{N}{K})
$$

ここで、$( N ) $は植物の個体数、$( t ) $は時間、$( r ) $は成長率、$ ( K ) $はキャリング・キャパシティ（環境が許容する最大個体数）を表します。

この方程式をPythonで解いてグラフ化するコードを以下に示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# ロジスティック成長曲線の微分方程式
def logistic_growth(t, N, r, K):
    return r * N * (1 - (N / K))

# パラメータ設定
r = 0.1  # 成長率
K = 100  # キャリング・キャパシティ

# 時間の範囲
t_span = (0, 50)
t_eval = np.linspace(*t_span, 100)

# 初期値
N0 = 10

# 微分方程式を解く
sol = solve_ivp(logistic_growth, t_span, [N0], t_eval=t_eval, args=(r, K))

# グラフ化
plt.figure(figsize=(8, 6))
plt.plot(sol.t, sol.y[0], label='Population Growth')
plt.title('Logistic Growth of Population')
plt.xlabel('Time')
plt.ylabel('Population Size')
plt.legend()
plt.grid(True)
plt.show()

このコードは、ロジスティック成長曲線の微分方程式を解いて、時間と個体数の関係をグラフ化します。

[実行結果]

ソースコード解説

このソースコードは、Pythonを使用してロジスティック成長曲線を解き、結果をグラフ化するプログラムです。

以下はそれぞれの部分の詳細な説明です：

ライブラリのインポート

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

• numpy：数値計算を行うためのライブラリ。
• matplotlib.pyplot：グラフ描画のためのライブラリ。
• scipy.integrate.solve_ivp：常微分方程式を解くための関数。

ロジスティック成長曲線の微分方程式の定義

1
2

def logistic_growth(t, N, r, K):
    return r * N * (1 - (N / K))

• logistic_growth 関数は、ロジスティック成長曲線の微分方程式を定義しています。
  この方程式は、成長率 r 、キャリング・キャパシティ K 、個体数 N に依存しています。

パラメータの設定

1
2

r = 0.1  # 成長率
K = 100  # キャリング・キャパシティ

• 成長率 r とキャリング・キャパシティ K の値を設定しています。

時間の範囲の設定

1
2

t_span = (0, 50)
t_eval = np.linspace(*t_span, 100)

• t_span には時間の範囲$ (0, 50) $が設定されています。
• t_eval はこの時間範囲を均等に分割した値の配列です。

初期値の設定

1

N0 = 10

• 初期の個体数 N0 を設定しています。

微分方程式の解を求める

1

sol = solve_ivp(logistic_growth, t_span, [N0], t_eval=t_eval, args=(r, K))

• solve_ivp 関数を使用して微分方程式を解きます。
• 引数として、微分方程式の定義、時間の範囲、初期値、その他の必要なパラメータを渡します。

グラフ化

1
2
3
4
5
6
7
8

plt.figure(figsize=(8, 6))
plt.plot(sol.t, sol.y[0], label='Population Growth')
plt.title('Logistic Growth of Population')
plt.xlabel('Time')
plt.ylabel('Population Size')
plt.legend()
plt.grid(True)
plt.show()

• matplotlib.pyplot を使用してグラフを作成します。
• sol.t と sol.y[0] によって、時間と個体数の解がプロットされます。
• グラフのタイトル、軸ラベル、凡例、グリッド線が追加されます。
• plt.show() によって、グラフが表示されます。

結果解説

[実行結果]

上記のグラフは、ロジスティック成長曲線を示しています。

以下はグラフの詳細な説明です：

x軸（横軸）：

時間を表します。
時間の範囲は$0$から$50$までです。

y軸（縦軸）：

個体数（植物の個体数など）を表します。
個体数の範囲は$0$から$100$までです。

線グラフ：

横軸（時間）に対する縦軸（個体数）の変化を表しています。

グラフのタイトル：

“Logistic Growth of Population” というタイトルが設定されています。

x軸のラベル：

“Time” というラベルが設定されており、時間を表しています。

y軸のラベル：

“Population Size” というラベルが設定されており、個体数を表しています。

凡例：

“Population Growth” という凡例が設定されています。
これは、線グラフが個体数の成長を表していることを示しています。

グリッド線：

背景にグリッド線が描かれており、グラフの読み取りを補助します。

このグラフは、時間が経つにつれて個体数がどのように変化するかを示しています。

最初は急速に増加しますが、キャリング・キャパシティに近づくにつれて成長が鈍化し、最終的に一定の値に収束します。

これは、ロジスティック成長曲線が、成長率による増加と環境の制約による減少のバランスを表現していることを示しています。