カルダノの公式（Cardano's formula）

カルダノの公式（Cardano's formula）

カルダノの公式（Cardano’s formula）は、2次方程式$ ( ax^2 + bx + c = 0 ) $の解の公式です。

この公式は以下のように表されます：

$$
x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}
$$

この公式をPythonで使用して、2次方程式の解を計算し、グラフ化する方法を示します。

まずは、必要なライブラリをインポートします。

1
2
import numpy as np
import matplotlib.pyplot as plt

次に、2次方程式の解を計算する関数を定義します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def solve_quadratic(a, b, c):
    discriminant = b**2 - 4*a*c  # 判別式を計算

    if discriminant > 0:
        # 2つの異なる実数解を持つ場合
        x1 = (-b + np.sqrt(discriminant)) / (2*a)
        x2 = (-b - np.sqrt(discriminant)) / (2*a)
        return x1, x2
    elif discriminant == 0:
        # 重解を持つ場合
        x = -b / (2*a)
        return x, x
    else:
        # 実数解を持たない場合
        return None

この関数 solve_quadratic は、2次方程式$ ( ax^2 + bx + c = 0 ) $の係数$ ( a, b, c ) $を受け取り、解を計算して返します。

解が実数の場合は$ ( (x_1, x_2) ) $の形で返し、重解の場合は$ ( (x, x) ) $の形で返します。

実数解が存在しない場合は None を返します。

次に、計算した解をグラフ化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def plot_quadratic_solution(a, b, c):
    x_values = np.linspace(-10, 10, 400)  # xの範囲を設定
    y_values = a*x_values**2 + b*x_values + c  # 2次方程式のグラフを作成

    plt.figure(figsize=(8, 6))
    plt.plot(x_values, y_values, label=f'{a}x^2 + {b}x + {c} = 0')  # 2次方程式のグラフをプロット

    # 解の計算
    solutions = solve_quadratic(a, b, c)
    if solutions:
        for solution in solutions:
            plt.plot(solution, 0, 'ro')  # 解を赤い点でプロット

    plt.title('Quadratic Equation')
    plt.xlabel('x')
    plt.ylabel('y')
    plt.legend()
    plt.grid(True)
    plt.axhline(0, color='black', linewidth=0.5)
    plt.axvline(0, color='black', linewidth=0.5)
    plt.show()

この関数 plot_quadratic_solution は、2次方程式のグラフを描画します。
2次方程式の解が存在する場合は、解を赤い点でプロットします。

これらの関数を使って、具体的な2次方程式を解いてグラフ化する例を示します。

1
2
3
4
5
6
7
# 例: 2x^2 - 5x + 2 = 0 の解とグラフ化
a = 2
b = -5
c = 2

# 2次方程式の解を計算し、グラフ化
plot_quadratic_solution(a, b, c)

この例では、2次方程式$ ( 2x^2 - 5x + 2 = 0 ) $の解を計算し、その解を含むグラフを描画しています。

他の2次方程式に対しても同様に関数を使用できます。

グラフ解説

[実行結果]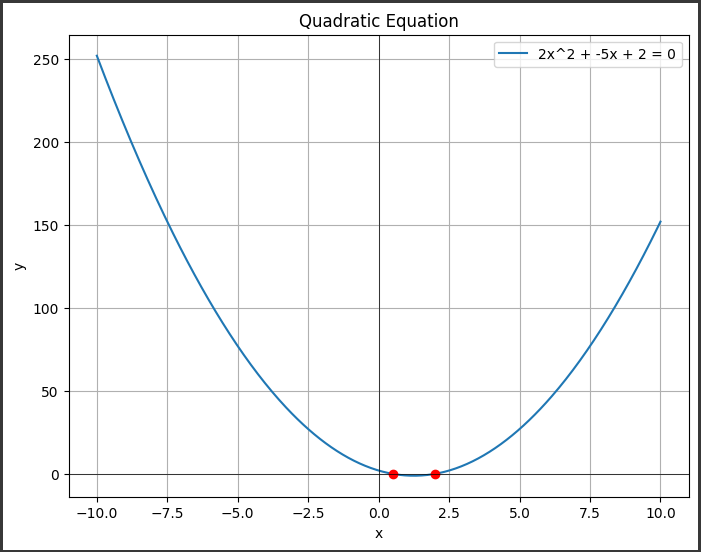

2次方程式$ ( ax^2 + bx + c = 0 ) $の解とそのグラフを詳しく説明します。

1. グラフの描画:

  • プロットされた曲線は、2次方程式$ ( y = ax^2 + bx + c ) $のグラフです。
    この曲線は放物線を表し、その形状は係数$ ( a, b, c ) $の値によって決まります。
  • 横軸$ ( x ) $は変数$ ( x ) $の値を示し、縦軸$ ( y ) $はそれに対応する2次方程式の値$ ( y ) $を表します。

2. 解の計算:

  • 2次方程式$ ( ax^2 + bx + c = 0 ) $の解は、$ ( x ) $の値で曲線が$ ( y = 0 ) $と交わる点です。
    これらの点が解を表します。
  • 解は関数 solve_quadratic(a, b, c) を用いて計算されます。
    解が実数解を持つ場合は$ ( (x_1, x_2) ) $の形で表示され、重解の場合は同じ$ ( x ) $の値が二つの解として示されます。

3. 解のプロット:

  • 計算された解は赤い点でグラフ上にプロットされます。
    これらの点は、2次方程式の解を示しています。
  • 解の点が曲線上にある場合は、それが方程式の解であることを示します。

4. 曲線の特徴:

  • 2次方程式の放物線は、係数$ ( a ) $によって開き方が異なります。
    $ ( a > 0 ) $の場合は上に凸の形状（頂点が最小値）、$ ( a < 0 ) $の場合は下に凸の形状（頂点が最大値）を示します。
  • 係数$ ( b ) $は曲線の位置を左右にシフトさせ、係数$ ( c ) $は曲線の位置を上下にシフトさせます。

5. グラフの表示:

  • グラフは横軸の範囲や解の位置によって、曲線の形状や解の配置が変わります。
  • 横軸の範囲は np.linspace() 関数によって設定され、解が存在する範囲や曲線の描画範囲が決まります。

これらの要素を組み合わせることで、2次方程式の解とそのグラフを理解することができます。

グラフは曲線の形状や解の位置を直感的に示し、数学的な関係を視覚的に理解するのに役立ちます。