連立方程式のグラフ化

連立方程式のグラフ化

連立方程式の解をグラフ化します。

ここでは、3変数の非線形連立方程式を解き、その解をグラフ化する例を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.optimize import fsolve

# 連立方程式を定義する関数
def equations(vars):
    x, y, z = vars
    eq1 = x**2 + y**2 + z**2 - 9
    eq2 = x**2 - y**2 + 2*z**2 - 4
    eq3 = 3*x**2 + y**2 - 2*z**2 - 12
    return [eq1, eq2, eq3]

# 初期値を設定
x0 = 1
y0 = 1
z0 = 1

# 連立方程式を解く
solution = fsolve(equations, [x0, y0, z0])
print(f"Solution: x={solution[0]:.3f}, y={solution[1]:.3f}, z={solution[2]:.3f}")

# グラフ化
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)

Z1 = np.sqrt(9 - X**2 - Y**2)
Z2 = np.sqrt((4 + Y**2 - X**2) / 2)
Z3 = np.sqrt((12 - 3*X**2 - Y**2) / 2)

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z1, alpha=0.5, color='r', label='eq1')
ax.plot_surface(X, Y, Z2, alpha=0.5, color='g', label='eq2')
ax.plot_surface(X, Y, Z3, alpha=0.5, color='b', label='eq3')
ax.scatter(solution[0], solution[1], solution[2], c='k', marker='o', s=50, label='Solution')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

このコードでは、3つの非線形方程式から成る連立方程式を定義しています。

$$
x^2 + y^2 + z^2 - 9 = 0
$$
$$
x^2 - y^2 + 2z^2 - 4 = 0
$$
$$
3x^2 + y^2 - 2z^2 - 12 = 0
$$

scipy.optimize.fsolve関数を使って、この連立方程式の解を数値的に求めています。

次に、meshgridを使って$x-y$平面上の点を生成し、各点における$z$値を3つの方程式から計算しています。
これらの点をplot_surfaceで3次元プロットしています。

最後に、連立方程式の解をscatterでプロットしています。

実行すると、以下のような3次元グラフが表示されます。
赤、緑、青の曲面が3つの方程式を表し、黒い点が連立方程式の解を表しています。

[実行結果]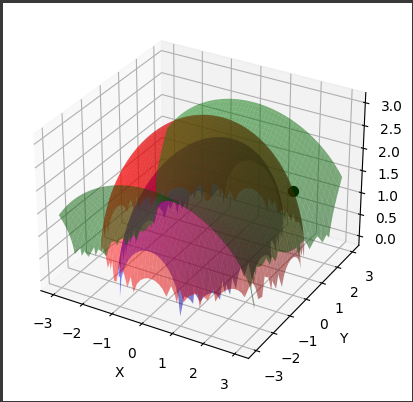

このようにPythonを使えば、複雑な連立方程式の解を視覚的に確認することができます。

ソースコード解説

ソースコードを詳しく説明します。

1. 必要なライブラリのインポート

1
2
3
4
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.optimize import fsolve
  • NumPyは数値計算ライブラリ。
  • MatplotlibはPythonでグラフを描くライブラリ。
  • mpl_toolkits.mplot3dは3次元プロットに必要。
  • scipy.optimizeからfsolve関数を使って連立方程式を解きます。

2. 連立方程式を定義する関数

1
2
3
4
5
6
def equations(vars):
    x, y, z = vars
    eq1 = x**2 + y**2 + z**2 - 9
    eq2 = x**2 - y**2 + 2*z**2 - 4
    eq3 = 3*x**2 + y**2 - 2*z**2 - 12
    return [eq1, eq2, eq3]
  • この関数は3変数$x$, $y$, $z$の非線形連立方程式を定義しています。
  • $eq1$, $eq2$, $eq3$がそれぞれの方程式。
  • リストとして[eq1, eq2, eq3]を返します。

3. 初期値の設定

1
2
3
x0 = 1
y0 = 1 
z0 = 1
  • 連立方程式を解くための初期値$x0$, $y0$, $z0$を設定しています。

4. 連立方程式の解を求める

1
2
solution = fsolve(equations, [x0, y0, z0])
print(f"Solution: x={solution[0]:.3f}, y={solution[1]:.3f}, z={solution[2]:.3f}")
  • fsolve関数に先程定義した方程式とベクトル$[x0, y0, z0]$を渡して解を求めます。
  • 解の$x$, $y$, $z$値をprintで出力します。

5. グラフ化の準備

1
2
3
4
5
6
7
x = np.linspace(-3, 3, 100)
y = np.linspace(-3, 3, 100)
X, Y = np.meshgrid(x, y)

Z1 = np.sqrt(9 - X**2 - Y**2)
Z2 = np.sqrt((4 + Y**2 - X**2) / 2)  
Z3 = np.sqrt((12 - 3*X**2 - Y**2) / 2)
  • $x$, $y$の範囲を$-3$から$3$まで$100$点に分けてリストを作成。
  • meshgridで$X$, $Y$の格子点を作成。
  • 3つの方程式からそれぞれ$Z1$, $Z2$, $Z3$を計算。

6. プロットとグラフの設定

1
2
3
4
5
6
7
8
9
10
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z1, alpha=0.5, color='r', label='eq1')
ax.plot_surface(X, Y, Z2, alpha=0.5, color='g', label='eq2')
ax.plot_surface(X, Y, Z3, alpha=0.5, color='b', label='eq3')
ax.scatter(solution[0], solution[1], solution[2], c='k', marker='o', s=50, label='Solution')
ax.set_xlabel('X')
ax.set_ylabel('Y') 
ax.set_zlabel('Z')
plt.show()
  • 新しい図とプロット領域を作成。
  • plot_surfaceで3つの曲面をプロット。
  • scatterでソリューションの点をプロット。
  • 軸ラベルを設定。
  • グラフを表示。

このコードでは、3変数の非線形連立方程式を定義し、その解を求めています。
その上で、解と3つの曲面を3次元プロットで可視化しています。

曲面の交点がちょうど解になっていることが一目でわかるグラフになっています。

結果解説

[実行結果]

この3次元グラフには以下の内容が表示されています。

1. 3つの曲面 (赤、緑、青)

  • これらは3つの連立方程式をそれぞれ表した曲面です。
  • 赤い曲面は $x^2 + y^2 + z^2 - 9 = 0$ を満たす点の集合。
  • 緑の曲面は $x^2 - y^2 + 2z^2 - 4 = 0$ を満たす点の集合。
  • 青の曲面は $3x^2 + y^2 - 2z^2 - 12 = 0$ を満たす点の集合。

2. 黒い点

  • この点が連立方程式の解$ (x, y, z) $を表しています。
  • 具体的な値は $x=1.826$, $y=-1.030$, $z=1.714$ です。
  • この点は3つの曲面が交わる点に位置しています。

3. 座標軸

  • $X$軸 (赤): $x$座標を表します。
  • $Y$軸 (緑): $y$座標を表します。
  • $Z$軸 (青): $z$座標を表します。

4. 曲面とグラフの範囲

  • $X$, $Y$軸方向に$-3$から$3$まで。
  • 曲面はこの範囲内で描かれています。

5. 透明度(alpha値)

  • 曲面には$0.5$の透明度が設定されています。
  • これにより、3つの曲面が重なる部分が見やすくなっています。

6. 凡例

  • 曲面の色と方程式の対応関係が示されています。
  • 黒い点が「Solution」と表示されています。

このように、この3次元グラフは与えられた3つの連立方程式の様子と、その解をわかりやすく可視化しています。

曲面の交点が連立方程式の解になっていることが一目でわかります。