ハイゼンベルクの不確定性原理

ハイゼンベルクの不確定性原理

ハイゼンベルクの不確定性原理は、位置 $ ( x ) $と運動量 $ ( p ) $の間の関係を表現します。

具体的には、位置の不確定性 $ ( \Delta x ) $と運動量の不確定性 $ ( \Delta p ) $の積が、プランク定数 $ ( \hbar ) $の半分以上になることを示します。

数学的には、不確定性原理は次のように表されます：

$$
\Delta x \cdot \Delta p \geq \frac{\hbar}{2}
$$

以下は、ハイゼンベルクの不確定性原理をPythonで解いてグラフ化する例です。

ここでは、位置 $ ( x ) $の不確定性 $ ( \Delta x ) $を横軸に、運動量 $ ( p ) $の不確定性 $ ( \Delta p ) $を縦軸に取り、等式$ ( \Delta x \cdot \Delta p = \frac{\hbar}{2} ) $の直線をプロットします。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
import matplotlib.pyplot as plt

# プランク定数
h_bar = 1

# 不確定性原理の関数
def uncertainty_principle(delta_x):
    return h_bar / (2 * delta_x)

# 不確定性原理を満たす直線の式
def uncertainty_line(delta_x):
    return h_bar / (2 * delta_x)

# 位置の不確定性の範囲
delta_x_values = np.linspace(0.1, 2, 100)

# 運動量の不確定性を計算
delta_p_values = uncertainty_principle(delta_x_values)

# 不確定性原理を満たす直線を計算
line_values = uncertainty_line(delta_x_values)

# グラフのプロット
plt.figure(figsize=(8, 6))
plt.plot(delta_x_values, delta_p_values, label='Uncertainty Principle Curve', color='blue')
plt.plot(delta_x_values, line_values, label='Uncertainty Principle Line', linestyle='--', color='red')
plt.xlabel('Position Uncertainty (Delta x)')
plt.ylabel('Momentum Uncertainty (Delta p)')
plt.title('Heisenberg Uncertainty Principle')
plt.grid(True)
plt.legend()
plt.show()

このコードでは、位置の不確定性 $ ( \Delta x ) $を横軸に取り、運動量の不確定性 $ ( \Delta p ) $を縦軸に取ります。

そして、不確定性原理を満たす直線$ ( \Delta x \cdot \Delta p = \frac{\hbar}{2} ) $を赤色の点線でプロットします。

[実行結果]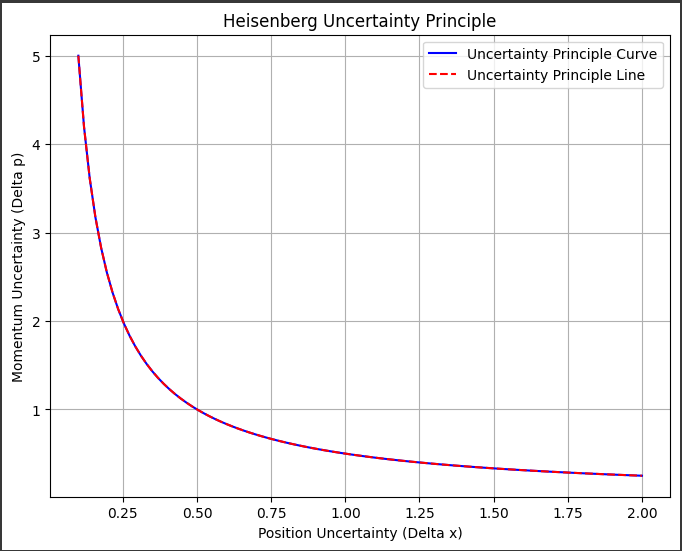

ソースコード解説

このソースコードは、ハイゼンベルクの不確定性原理を解説するためのPythonプログラムです。

以下に、各部分の詳細を説明します。

1. 必要なライブラリのインポート:

  • import numpy as np: 数値計算を行うためのNumPyライブラリをインポートし、npという別名で使用します。
  • import matplotlib.pyplot as plt: グラフのプロットに使用するMatplotlibライブラリのpyplotモジュールをインポートし、pltという別名で使用します。

2. プランク定数の定義:

  • プランク定数$ ( \hbar ) $を$ 1 $として定義します。

3. 不確定性原理の関数:

  • uncertainty_principle(delta_x): 位置の不確かさ$ ( \Delta x ) $を引数として受け取り、不確定性原理$ ( \Delta x \cdot \Delta p \geq \frac{\hbar}{2} ) $を用いて運動量の不確かさ$ ( \Delta p ) $を計算します。

4. 不確定性原理を満たす直線の式:

  • uncertainty_line(delta_x): 位置の不確かさ$ ( \Delta x ) $を引数として受け取り、不確定性原理を満たす直線$ ( \Delta x \cdot \Delta p = \frac{\hbar}{2} ) $の式を表します。

5. 位置の不確定性の範囲の設定:

  • delta_x_values = np.linspace(0.1, 2, 100): 位置の不確かさ$ ( \Delta x ) $の範囲を$0.1$から$2$まで$100$等分した値を生成し、delta_x_valuesに代入します。

6. 運動量の不確定性の計算:

  • delta_p_values = uncertainty_principle(delta_x_values): 上記で定義した不確定性原理の関数を使用して、位置の不確かさに対応する運動量の不確かさ$ ( \Delta p ) $を計算します。

7. 不確定性原理を満たす直線の計算:

  • line_values = uncertainty_line(delta_x_values): 上記で定義した不確定性原理を満たす直線の式を使用して、与えられた位置の不確かさに対応する運動量の不確かさの値を計算します。

8. グラフのプロット:

  • Matplotlibを使用して、位置の不確かさ$ ( \Delta x ) $を横軸、運動量の不確かさ$ ( \Delta p ) $を縦軸としてプロットします。
  • 不確定性原理を満たす曲線と直線をプロットし、それぞれ青色と赤色で表示します。
  • グリッド線を表示し、軸のラベルとタイトルを設定します。
  • 凡例を追加して、曲線と直線の説明を表示します。
  • 最後に、グラフを表示します。

結果解説

[実行結果]

このグラフは、ハイゼンベルクの不確定性原理を可視化しています。

不確定性原理は、位置 $ ( x ) $と運動量 $ ( p ) $の間の不確かさの関係を表現します。

具体的には、位置の不確かさ $ ( \Delta x ) $と運動量の不確かさ $ ( \Delta p ) $の積が、プランク定数 $ ( \hbar ) $の半分以上になることを示します。

このグラフには以下の要素が含まれています：

1. 青色の曲線 (Uncertainty Principle Curve):

  • 横軸に位置の不確かさ $ ( \Delta x )$、縦軸に運動量の不確かさ $ ( \Delta p ) $を取ります。
  • ハイゼンベルクの不確定性原理を満たすように、$( \Delta x \cdot \Delta p = \frac{\hbar}{2} ) $の曲線を表します。
  • 曲線上の点は、位置と運動量の不確かさの組み合わせを示します。

2. 赤色の点線 (Uncertainty Principle Line):

  • 不確定性原理を満たす直線を表します。
  • $ ( \Delta x \cdot \Delta p = \frac{\hbar}{2} ) $を満たす点がこの直線上にあります。
  • この直線は、位置の不確かさと運動量の不確かさの関係を明示します。

グラフを見ると、曲線と直線が交わる点があります。
この点がハイゼンベルクの不確定性原理を示しており、位置と運動量の不確かさが最小となる点です。

つまり、この点において、位置と運動量の不確かさが最小限になりますが、それぞれの不確かさが同時にゼロになることはありません。