モビウス帯方程式

モビウス帯方程式

モビウス帯方程式は、三次元空間内に特殊な帯状の曲面を定義するための方程式です。

モビウス帯は、帯状の面が一度だけねじれている特殊な形状を持つことで知られています。

モビウス帯方程式は以下のように表されます：

x=(1+v2cos(u2))cos(u)


y=(1+v2cos(u2))sin(u)

z=v2sin(u2)

ここで、(u)と(v)はパラメータであり、それぞれ帯の周りの角度と帯の幅を表します。
これらのパラメータによって、曲面上の各点の座標(x,y,z)が計算されます。

この方程式によって定義されるモビウス帯は、その特異な形状から幾何学や数学の興味深いトピックとなっています。

また、この帯の特性は、科学や工学の様々な分野で興味深い応用が見られます。

ソースコード

Pythonでこれを解いてグラフ化するには、Matplotlibを使用します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# パラメータの範囲
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(-1, 1, 100)
U, V = np.meshgrid(u, v)

# モビウス帯方程式の解
x = (1 + V/2 * np.cos(U/2)) * np.cos(U)
y = (1 + V/2 * np.cos(U/2)) * np.sin(U)
z = V/2 * np.sin(U/2)

# 3Dプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')

# 軸ラベルの設定
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

# グラフの表示
plt.show()

このコードでは、指定されたパラメータ範囲内で(x)、(y)、(z)の値を計算し、それを3Dプロットとして描画しています。

[実行結果]

ソースコード解説

ソースコードの各部分を説明します。

ライブラリのインポート

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  • numpy：数値計算ライブラリ。
    多次元配列や行列演算などを提供する。
  • matplotlib.pyplot：グラフ描画ライブラリ。
    2次元プロットや3次元プロットを描画するために使用される。
  • mpl_toolkits.mplot3d.Axes3D：3次元プロットのためのサブモジュール。

パラメータの範囲の設定

1
2
3
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(-1, 1, 100)
U, V = np.meshgrid(u, v)
  • u：パラメータ(u)の範囲を設定。
    0から(2π)までの範囲を100個の等間隔に区切る。
  • v：パラメータ(v)の範囲を設定。
    −1から1までの範囲を100個の等間隔に区切る。
  • np.meshgrid(u, v)：パラメータ(u)と(v)を組み合わせたメッシュグリッドを作成する。

モビウス帯方程式の解の計算

1
2
3
x = (1 + V/2 * np.cos(U/2)) * np.cos(U)
y = (1 + V/2 * np.cos(U/2)) * np.sin(U)
z = V/2 * np.sin(U/2)
  • モビウス帯方程式から(x)、(y)、(z)の座標を計算する。

3Dプロットの設定

1
2
3
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')
  • 3Dプロットを描画するための設定を行う。
  • fig：新しいFigureオブジェクトを作成。
  • ax：3Dサブプロットを作成し、現在のFigureに追加。
  • ax.plot_surface(x, y, z, cmap='viridis')：モビウス帯の表面をプロットする。

軸ラベルの設定

1
2
3
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
  • 軸ラベルを設定する。

グラフの表示

1
plt.show()
  • 設定したグラフを表示する。

グラフ解説

[実行結果]

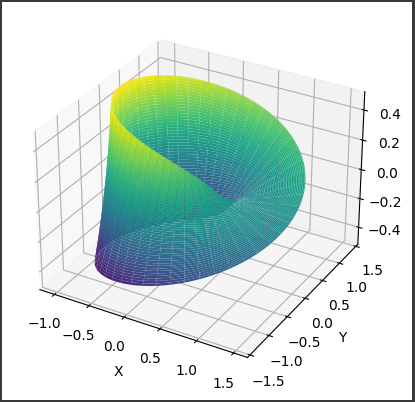
このグラフは、モビウス帯を表現しています。
モビウス帯は特殊な形状であり、帯状の面が一度だけねじれているものです。
具体的には、帯の中心を一周しても片側だけが反転するという特性を持っています。

このグラフでは、三次元空間内にモビウス帯が描かれています。
各点はパラメータ(u)と(v)によって定義され、それに対応する(x)、(y)、(z)座標が計算されています。

  • (x)、(y)、(z)軸はそれぞれ三次元空間内の座標を表します。
  • 曲面は帯状であり、一見すると通常の帯のように見えますが、実際には一周してねじれていることが分かります。
  • 曲面の色は ‘viridis’ カラーマップに基づいて決定され、高さや深さを視覚的に表現しています。

このグラフは、モビウス帯の特徴を視覚的に理解するのに役立ちます。