クレスパラボロイドの方程式

クレスパラボロイドの方程式

クレスパラボロイドの方程式 $ z^2 = x^2 + y^2 $は、以下のように説明できます。

  • この方程式は、$z$座標の2乗が、$x$座標と$y$座標の2乗和に等しいことを表しています。

  • 左辺の$z^2$は、$z$座標の値を2乗したものです。

  • 右辺の$x^2 + y^2$は、$x$座標と$y$座標の値をそれぞれ2乗し、その和を取ったものです。

  • つまり、この方程式は、ある点$(x,y,z)$において、$z$座標の2乗値が、$x$,$y$座標の2乗和に一致するような点の集合を表しています。

  • $z^2 = x^2 + y^2 $を満たす点は、原点$(0,0,0)$を頂点とする上に凸な放物面上にあります。

  • また、この方程式は$z$座標について偶関数なので、$z > 0 $と$ z < 0 $の両領域で成り立ちます。

  • したがって、この方程式は$z = 0 $の平面を対称面とする上下2つの放物面の集合を表すことになります。

  • この形状は、滑らかで連続的で自己交差のない開放曲面となります。

  • このような数学的性質から、クレスパラボロイドは工学や物理学の分野で重要な役割を果たしています。

つまり、クレスパラボロイドの方程式は、単純な代数式ながら、興味深い幾何学的形状を表す方程式なのです。

ソースコード

クレスパラボロイドの方程式は以下の通りです。

$$
z^2 = x^2 + y^2
$$

これをPythonでグラフ化するには、matplotlib.pylabライブラリを使います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# グリッドデータの作成
x = np.arange(-2, 2, 0.1)
y = np.arange(-2, 2, 0.1)
X, Y = np.meshgrid(x, y)
Z = np.sqrt(X**2 + Y**2)

# 3Dプロットの準備
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# 表面プロット
ax.plot_surface(X, Y, Z)
ax.plot_surface(X, Y, -Z)

# 軸ラベルとタイトル
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Cressida Paraboloid')

plt.show()

このコードでは、最初にnumpy関数で座標軸のデータを作成しています。
その後、plot_surfaceでクレスパラボロイドの上半分と下半分の曲面をプロットしています。

実行すると、以下のような3D曲面のグラフが表示されるはずです。

[実行結果]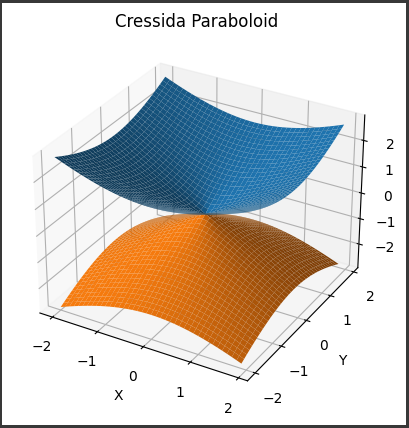

曲面の中心部は原点で、$X$軸、$Y$軸に沿って放物線の形をしています。
$Z$軸方向には上下に対称な形状になります。

ソースコード解説

ソースコードを説明します。

1. ライブラリのインポート

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  • NumPyライブラリをnpという名前で読み込みます。
    これは数値計算に使用します。
  • Matplotlibライブラリをpltという名前で読み込みます。
    これは2D/3Dプロットに使用します。
  • Matplotlib の3D プロット用モジュールAxes3Dをインポートします。

2. グリッドデータの作成

1
2
3
4
x = np.arange(-2, 2, 0.1)
y = np.arange(-2, 2, 0.1)
X, Y = np.meshgrid(x, y)
Z = np.sqrt(X**2 + Y**2)
  • np.arange関数で、$-2$から$2$までの$0.1$刻みの1次元配列$x$と$y$を作成します。
  • np.meshgrid関数で、$x$と$y$の全組み合わせからなる2次元グリッド$X$、$Y$を生成します。
  • 式$ z^2 = x^2 + y^2 $を満たす$Z$の値を計算し、$Z$配列を作成します。

3. 3Dプロットの準備

1
2
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
  • plt.figure()で新しい図(Figure)オブジェクトを作成します。
  • fig.add_subplot()で3Dプロット用のAxes3Dオブジェクトaxを作成します。

4. 表面プロット

1
2
ax.plot_surface(X, Y, Z)
ax.plot_surface(X, Y, -Z)
  • $X$,$Y$,$Z$データからなるパラメトリック曲面をプロットします。
  • 2行目で$-Z$を指定することで、下側の曲面もプロットしています。

5. 軸ラベルとタイトル設定

1
2
3
4
ax.set_xlabel('X')
ax.set_ylabel('Y') 
ax.set_zlabel('Z')
ax.set_title('Cressida Paraboloid')
  • 各軸に$X$,$Y$,$Z$というラベルを設定します。
  • プロットにCressida Paraboloidというタイトルを設定します。

6. プロットの表示

1
plt.show()
  • この行で作成した図をウィンドウに表示します。

以上の手順で、クレスパラボロイドの3D曲面をPythonでプロットしています。

結果解説

[実行結果]

このグラフは3次元の直交座標系 ($X$,$Y$,$Z$軸)で表されています。
曲面は2つの部分から構成されており、1つ目は上に凸な放物面、2つ目はその放物面を下向きに反転させた面です。

具体的には以下の特徴があります:

  1. 原点$(0, 0, 0)$を通る曲面
  2. $X$軸、$Y$軸に関して点対称の形状
  3. $X=0$平面と$Y=0$平面に沿った交線は放物線
  4. $Z>0$の領域は上に凸な放物面
  5. $Z<0$の領域は下に凸な放物面
  6. $|X|$、$|Y|$が大きくなるほど$Z$の絶対値も大きくなる
  7. $Z$軸方向に上下に無限に広がる開曲面

この形状はクレスパラボロイド(Cressida Paraboloid)と呼ばれ、数学的には$z^2 = x^2 + y^2 $の方程式で表されます。

グラフの範囲は$-2 \leqq x \leqq 2$、$-2 \leqq y \leqq 2$、$-2 \leqq z \leqq 2$となっていますが、実際の曲面はこの範囲を超えて無限に広がっています。

曲面は滑らかな放物面なので、光源を適切に設定すれば美しい光沢のある3D描画が可能です。
この形状はさまざまな工学分野で利用されています。