リーマンゼータ関数

2月 20, 2024

リーマンゼータ関数

３次元方程式の一例として、リーマンゼータ関数のモジュラー形式が挙げられます。

リーマンゼータ関数は複素数$ (s) $に対して次のように定義されます。

$$
\zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s}
$$

モジュラー形式についての厳密な表現は複雑ですが、その近似式として次のような方程式があります。

$$
f(x, y) = \sum_{n=1}^{\infty} \left( \frac{1}{n^{2 + ix}} + \frac{1}{n^{2 - ix}} \right) \cos\left( \frac{n\pi y}{2} \right)
$$

これをPythonで解き、3Dグラフ化するコードを以下に示します。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# リーマンゼータ関数のモジュラー形式の近似式
def zeta_function(x, y, terms=100):
    result = 0
    for n in range(1, terms + 1):
        result += (1 / (n ** (2 + 1j * x)) + 1 / (n ** (2 - 1j * x))) * np.cos(n * np.pi * y / 2)
    return np.real(result)

# x, y の値の範囲
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)

# リーマンゼータ関数のモジュラー形式の値を計算
Z = zeta_function(X, Y)

# 3Dグラフの描画
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Zeta Function (Modular Form)')
plt.show()

このコードは、リーマンゼータ関数のモジュラー形式の近似式を計算し、3Dグラフで可視化します。

[実行結果]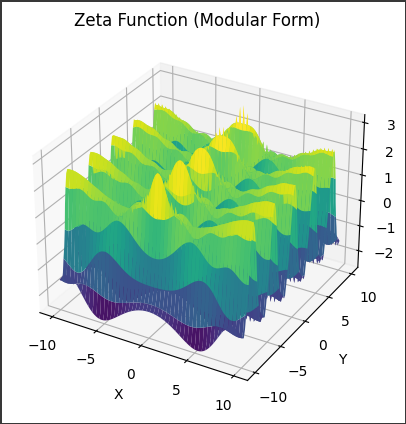

ソースコード解説

以下にコードの詳細な説明を示します。

1. NumPyとMatplotlibのインポート:

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

numpy は数値計算を行うためのライブラリです。
matplotlib.pyplot はグラフの描画に使用されるライブラリです。
mpl_toolkits.mplot3d は3Dグラフの描画に必要なツールキットです。

2. リーマンゼータ関数のモジュラー形式の近似式:

def zeta_function(x, y, terms=100):
   result = 0
   for n in range(1, terms + 1):
       result += (1 / (n ** (2 + 1j * x)) + 1 / (n ** (2 - 1j * x))) * np.cos(n * np.pi * y / 2)
   return np.real(result)

zeta_function 関数は、リーマンゼータ関数のモジュラー形式の近似式を計算します。
近似式は、$(x) $と$ (y) $の２つの変数に依存します。
近似式は、与えられた$ (x) $と$ (y) $の値に対して計算され、その結果が result に保存されます。

3. x, y の値の範囲の設定:

1
2
3

x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)

np.linspace() 関数は、指定された範囲内で等間隔の数値配列を生成します。
ここでは、$-10$から$10$までの範囲を$100$分割した値を生成しています。
np.meshgrid() 関数は、２つの1次元配列から格子状の座標を生成します。
ここでは、$x$ と$ y $の値の組み合わせを格納する X と Y を生成しています。

4. リーマンゼータ関数のモジュラー形式の値を計算:

1	Z = zeta_function(X, Y)

zeta_function 関数を用いて、各点$ (x, y) $におけるリーマンゼータ関数のモジュラー形式の近似値を計算し、Z に保存します。

5. 3Dグラフの描画:

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Zeta Function (Modular Form)')
plt.show()

plt.figure() で新しい図を生成し、fig に保存します。
fig.add_subplot(111, projection='3d') で3Dサブプロットを生成し、ax に保存します。
ax.plot_surface() で3Dサーフェスプロットを描画します。ここでは、$ (x) $、$ (y) $、$ (z) $の値が X、Y、Z に格納されていると仮定しています。
ax.set_xlabel()、ax.set_ylabel()、ax.set_zlabel() でそれぞれ軸ラベルを設定します。
ax.set_title() でグラフのタイトルを設定します。
plt.show() でグラフを表示します。

結果解説

[実行結果]

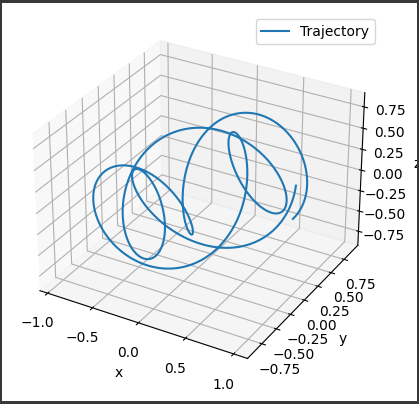
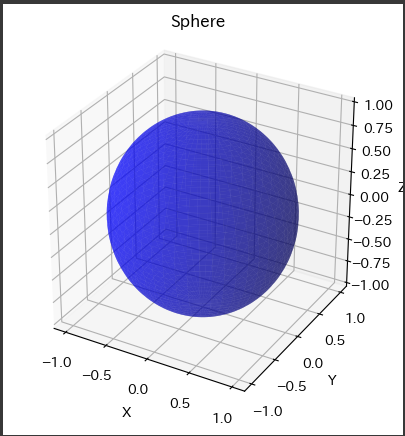
このグラフは、リーマンゼータ関数のモジュラー形式の近似式に基づいて描かれています。
リーマンゼータ関数は数学的に興味深い関数であり、数論や解析数学などの分野で重要な役割を果たしています。

具体的には、グラフは３次元空間上に描かれており、横軸は$(x)$、縦軸は$(y)$となっています。
そして、それぞれの点$(x, y)$における関数の値が、高さ方向に表されています。

リーマンゼータ関数のモジュラー形式は、$(x)$と$(y)$の２つの変数に依存する関数であり、その表現は複雑です。
このグラフでは、$(x)$と$(y)$の値が与えられたときの関数の値が色で表現されています。
色の濃淡は関数の値の大きさを示しており、明るい色ほど関数の値が大きく、暗い色ほど関数の値が小さいことを意味します。

リーマンゼータ関数は数学的に興味深い特性を持ち、特にリーマン予想と呼ばれる未解決問題との関連があります。
このグラフは、そのような数学的な概念を視覚的に理解する手助けとなることができます。

連立微分方程式

2月 19, 2024

連立微分方程式

4次元方程式の例として、次の連立微分方程式を考えます。

$$
\frac{dx}{dt} = -y
$$
$$
\frac{dy}{dt} = x - z
$$
$$
\frac{dz}{dt} = y - w
$$
$$
\frac{dw}{dt} = z
$$

これは、$(x)$、$(y)$、$(z)$、$(w)$の4つの変数を持つ4次元方程式です。

それでは、この方程式をPythonで解いてグラフ化しましょう。

以下がコードです。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# 4次元微分方程式
def equations(t, y):
    x, y, z, w = y
    dxdt = -y
    dydt = x - z
    dzdt = y - w
    dwdt = z
    return [dxdt, dydt, dzdt, dwdt]

# 初期条件と時間の設定
t_span = (0, 20)
t_eval = np.linspace(*t_span, 1000)
y0 = [1, 0, 0, 0]

# 方程式を解く
sol = solve_ivp(equations, t_span, y0, t_eval=t_eval)

# 結果をプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(sol.y[0], sol.y[1], sol.y[2], label='Trajectory')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.legend()
plt.show()

このコードは、4次元微分方程式を解き、その解を3次元空間上の軌跡としてグラフにプロットします。

[実行結果]

ソースコード解説

以下に、ソースコードの詳細な説明を示します。

1. ライブラリのインポート

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

NumPyは数値計算を行うためのライブラリ、Matplotlibはグラフ描画を行うためのライブラリ、scipy.integrateモジュールのsolve_ivp関数は常微分方程式を解くために使用されます。

2. 4次元微分方程式の定義

def equations(t, y):
    x, y, z, w = y
    dxdt = -y
    dydt = x - z
    dzdt = y - w
    dwdt = z
    return [dxdt, dydt, dzdt, dwdt]

equations関数では、4つの変数$ (x)$,$ (y)$,$ (z)$,$ (w) $に対する4次元微分方程式が定義されています。

3. 初期条件と時間の設定

1
2
3

t_span = (0, 20)
t_eval = np.linspace(*t_span, 1000)
y0 = [1, 0, 0, 0]

t_spanでは時間の範囲を指定し、t_evalではその範囲内で解を評価する時間の配列を生成します。
y0は初期条件を表し、この場合は$ (x = 1)$,$ (y = 0)$,$ (z = 0)$,$ (w = 0) $としています。

4. 方程式を解く

1	sol = solve_ivp(equations, t_span, y0, t_eval=t_eval)

solve_ivp関数を使用して微分方程式を解きます。
equations関数で定義された微分方程式、初期条件y0、評価する時間t_evalを引数として渡します。

5. 結果をプロット

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(sol.y[0], sol.y[1], sol.y[2], label='Trajectory')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.legend()
plt.show()

解析結果を3次元グラフにプロットします。
sol.yは解の配列で、sol.y[0]、sol.y[1]、sol.y[2]はそれぞれ$ (x)$、$(y)$、$(z)$の解を表します。

これを用いて3次元軌跡をプロットし、$x軸$、$y軸$、$z軸$にラベルを付けています。

結果解説

[実行結果]

このグラフは、4次元微分方程式の解を表す3次元の軌跡を示しています。

具体的には、$(x)$、$(y)$、$(z)$の3つの変数が時間に対してどのように変化するかを可視化しています。

$x軸$は変数$(x)$の値を表し、$y軸$は変数$(y)$の値を表します。
$z軸$は変数$(z)$の値を表しています。
しかし、実際には4次元方程式を解いているため、$(w)$変数の値が$z軸$に関連付けられます。
これは、3次元の空間で4次元方程式の解をプロットするための折衷案です。
軌跡は、初期条件から始まり、時間とともに変化する解の経路を示しています。
解の軌跡がどのように変化するかによって、4次元方程式の動的な振る舞いを視覚的に理解することができます。

このグラフは、4次元の微分方程式を解析する際に、解の性質や振る舞いを視覚化するのに役立ちます。

オイラー法

2月 18, 2024

数理解析の例題として、オイラー法による2階常微分方程式の解法をPythonで解き、グラフ化することを考えます。

この問題は、物理的シミュレーションや工学の問題など、様々な分野で使用されます。

まず、オイラー法による2階常微分方程式の解法について説明します。
オイラー法は、微分方程式を数値的に解くための方法で、特に時間に依存する物理現象を模擬する際によく使用されます。
この方法では、微分方程式を一連の一階の微分方程式に変換し、それぞれを個別に解いていきます

Pythonでこの問題を解くためには、以下の手順を踏むことになります。

時間の上限$T$と時間刻み幅$h$を定義します。
解を保存するための配列$y1[N+1]$,$ y2[N+1]$,$ t[N+1]$を用意します。
微分方程式を満たす関数$f1(t,y1,y2)$, $f2(t,y1,y2)$を定義します。
初期条件$y1[0] = a1$,$ y2[0] = a2$, $t[0] = 0$を設定します。
時間刻み幅$h$で時間tを進めながら、各時点での解を計算し、配列に保存します。
最後に、matplotlibを使用して計算結果をグラフ化します

以下に、これらの手順を実装したPythonコードを示します。

import numpy as np
import matplotlib.pyplot as plt

# 定数と初期条件を設定
T = 10
h = 0.01
a1 = 1
a2 = 0

# 配列を用意
y1 = np.zeros(int(T/h)+1)
y2 = np.zeros(int(T/h)+1)
t = np.zeros(int(T/h)+1)

# 微分方程式を満たす関数を定義
def f1(t, y1, y2):
    return y2

def f2(t, y1, y2):
    return -y1

# 初期条件を設定
y1[0] = a1
y2[0] = a2
t[0] = 0

# 時間を進めながら解を計算
for j in range(1, int(T/h)+1):
    t[j] = j*h
    y1[j] = y1[j-1] + h*f1(t[j-1], y1[j-1], y2[j-1])
    y2[j] = y2[j-1] + h*f2(t[j-1], y1[j-1], y2[j-1])

# 結果をグラフ化
plt.figure()
plt.plot(t, y1, label='y1')
plt.plot(t, y2, label='y2')
plt.legend()
plt.show()

このコードは、オイラー法を用いて2階常微分方程式を解き、結果をグラフ化するものです。

微分方程式の形式や初期条件、時間の上限$T$、時間刻み幅$h$は任意に変更することができます。

[実行結果]

ソースコード解説

このソースコードは、2つの連立常微分方程式を数値的に解いてその解をグラフにプロットするプログラムです。

以下にプログラムの詳細な説明を示します：

1. ライブラリのインポート

1 2	import numpy as np import matplotlib.pyplot as plt

NumPyとMatplotlibをインポートしています。
NumPyは数値計算のためのライブラリであり、Matplotlibはグラフ描画のためのライブラリです。

2. 定数と初期条件の設定

T = 10
h = 0.01
a1 = 1
a2 = 0

解析のための定数や初期条件を設定しています。
ここでは、解析する時間の範囲を表す$T$、時間の刻み幅を表す$h$、初期値$a1$と$a2$を設定しています。

3. 配列の準備

1
2
3

y1 = np.zeros(int(T/h)+1)
y2 = np.zeros(int(T/h)+1)
t = np.zeros(int(T/h)+1)

計算結果を格納するための配列$ y1$,$ y2$,$ t $を用意しています。
これらの配列は、時間の刻み幅$h$に基づいて計算される結果を保持します。

4. 微分方程式を満たす関数の定義

def f1(t, y1, y2):
    return y2

def f2(t, y1, y2):
    return -y1

解きたい連立常微分方程式を満たす関数$ f1$, $f2 $を定義しています。
この例では、1つ目の方程式が$dy1/dt = y2$、2つ目の方程式が$dy2/dt = -y1$に対応しています。

5. 初期条件の設定

1
2
3

y1[0] = a1
y2[0] = a2
t[0] = 0

初期条件を配列に設定しています。

6. 時間を進めながら解を計算

for j in range(1, int(T/h)+1):
    t[j] = j*h
    y1[j] = y1[j-1] + h*f1(t[j-1], y1[j-1], y2[j-1])
    y2[j] = y2[j-1] + h*f2(t[j-1], y1[j-1], y2[j-1])

Eulerの方法を使用して、連立常微分方程式を数値的に解いています。
時間を進めながら、前の時間ステップの解を使用して次の解を計算します。

7. 結果のグラフ化

plt.figure()
plt.plot(t, y1, label='y1')
plt.plot(t, y2, label='y2')
plt.legend()
plt.show()

得られた解をMatplotlibを使用してグラフにプロットし、$y1$曲線と$y2$曲線を表示しています。
$y1$曲線は青色で、$y2$曲線はオレンジ色で表されます。

結果解説

[実行結果]

このグラフは、2つの曲線で構成されています。

1. $ y1 $曲線:

この曲線は、時間に対する$ (y1) $の値を表しています。
最初は初期値$ (a1) $から始まり、時間とともに変化します。
曲線の形状は、微分方程式$ (\frac{dy1}{dt} = y2) $に基づいて決定されます。
$ (y2) $の値が変化すると、$ (y1) $の変化速度も変わります。

2. $ y2 $曲線:

この曲線は、時間に対する$ (y2) $の値を表しています。
同様に、初期値$ (a2) $から始まり、時間とともに変化します。
曲線の形状は、微分方程式$ (\frac{dy2}{dt} = -y1) $に基づいて決定されます。
$ (y1) $の値が変化すると、$ (y2) $の変化速度も変わります。

このグラフを通じて、2つの関数$ (y1) $と$ (y2) $が時間の経過とともにどのように振る舞うかを視覚的に理解できます。

複利計算

2月 17, 2024

複利計算

投資に関する方程式の例として、単純な複利計算を考えてみましょう。

複利計算の方程式は以下のように表されます:

$$
A = P \times (1 + r)^n
$$

$ (A) $は最終的な金額（将来価値）
$ (P) $は元本（現在価値）
$ (r) $は年利率
$ (n) $は投資期間（年数）

これをPythonで解き、グラフ化する方法を示します。

import numpy as np
import matplotlib.pyplot as plt

def compound_interest(P, r, n):
    """
    複利計算を行う関数
    
    Parameters:
        P (float): 元本（現在価値）
        r (float): 年利率
        n (int): 投資期間（年数）
    
    Returns:
        np.ndarray: 各年の金額の配列
    """
    years = np.arange(1, n+1)
    A = P * (1 + r)**years
    return A

# パラメータの設定
P = 1000  # 元本
r = 0.05  # 年利率 (5%)
n = 10    # 投資期間（10年）

# 複利計算を実行
investment_values = compound_interest(P, r, n)

# グラフの描画
plt.plot(np.arange(1, n+1), investment_values, marker='o')
plt.title('Compound Interest over {} Years'.format(n))
plt.xlabel('Years')
plt.ylabel('Investment Value')
plt.grid(True)
plt.show()

このコードは、元本$ (P) $、年利率$ (r) $、投資期間$ (n) $を与えられたときに、各年の投資金額$ (A) $を計算し、それをグラフ化しています。

[実行結果]

ソースコード解説

このソースコードは、Pythonを使用して複利計算を行い、その結果をグラフ化するプログラムです。

以下では、各部分の詳細を説明します。

ライブラリのインポート

1 2	import numpy as np import matplotlib.pyplot as plt

numpy は数値計算を行うためのライブラリです。
ここでは主に配列操作や数学的な計算に使用されます。
matplotlib.pyplot はグラフの描画に使用されるライブラリです。
plt として一般的にエイリアスされます。

複利計算の関数定義

def compound_interest(P, r, n):
    """
    複利計算を行う関数
    
    Parameters:
        P (float): 元本（現在価値）
        r (float): 年利率
        n (int): 投資期間（年数）
    
    Returns:
        np.ndarray: 各年の金額の配列
    """
    years = np.arange(1, n+1)
    A = P * (1 + r)**years
    return A

compound_interest 関数は、与えられた元本$ (P) $、年利率$ (r) $、投資期間$ (n) $に基づいて複利計算を行います。
各年の金額の配列を返します。

パラメータの設定

1
2
3

P = 1000  # 元本
r = 0.05  # 年利率 (5%)
n = 10    # 投資期間（10年）

P は元本（投資の始めの金額）を表します。
r は年利率を表します。ここでは$ 5% $を表す$ 0.05 $が設定されています。
n は投資期間（年数）を表します。ここでは$ 10 $年が設定されています。

複利計算の実行

1	investment_values = compound_interest(P, r, n)

compound_interest 関数を使用して、指定されたパラメータで複利計算を実行し、各年の金額の配列を取得します。

グラフの描画

plt.plot(np.arange(1, n+1), investment_values, marker='o')
plt.title('Compound Interest over {} Years'.format(n))
plt.xlabel('Years')
plt.ylabel('Investment Value')
plt.grid(True)
plt.show()

plt.plot() は、与えられたデータをプロットしてグラフを作成します。
ここでは、各年の金額の配列を横軸に対してプロットしています。
plt.title() はグラフのタイトルを設定します。
plt.xlabel() と plt.ylabel() はそれぞれ横軸と縦軸のラベルを設定します。
plt.grid(True) はグリッド線を表示します。
plt.show() は、グラフを表示します。

これにより、元本$ (P) $を元にした複利計算の結果が$ 10 $年間の投資期間にわたってグラフ化されます。

結果解説

[実行結果]

このグラフは、投資の元本$ (P) $、年利率$ (r) $、投資期間$ (n) $に基づいて計算された複利効果を示しています。

横軸は時間を表し、投資期間が経過するにつれて増加します。
縦軸は投資の価値を表し、元本$ (P) $から始まり、時間が経つにつれて複利効果により増加していきます。

具体的には、投資期間の各年における投資の価値が点で示されています。
この点は、元本$ (P) $を年利率$ (r) $で複利計算した結果を示しています。
グラフ全体として、時間が経過するにつれて投資の価値が増加していく様子が視覚化されています。

グラフのタイトルには、投資期間が何年かが示されており、横軸には各年が、縦軸には投資の価値がラベル付けされています。
また、グリッド線が描かれており、各年ごとの価値を読み取りやすくしています。

このグラフは、投資が時間の経過とともにどのように成長するかを視覚的に理解するのに役立ちます。

動力学

2月 16, 2024

動力学

航空学に関連する方程式の例としては、航空機の上昇および降下の動力学を記述するための運動方程式があります。

典型的な航空機の運動方程式は、重力、揚力、抗力、推力などの力を考慮しています。

以下に、簡単なモデルとして航空機の上昇と降下を表現する方程式を示します。

運動方程式：$ ( F = m \cdot a ) $
揚力（Lift）：$ ( L = \frac{1}{2} \cdot C_L \cdot \rho \cdot V^2 \cdot S ) $
重力（Gravity）：$ ( W = m \cdot g ) $
抗力（Drag）：$ ( D = \frac{1}{2} \cdot C_D \cdot \rho \cdot V^2 \cdot S ) $
推力（Thrust）：$ ( T ) $

これらの方程式を組み合わせて、航空機の上昇および降下の挙動をモデル化します。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# 航空機の運動方程式を定義
def aircraft_motion_equation(state, t, thrust, drag_coefficient, lift_coefficient, mass, gravity):
    # 状態変数
    altitude, velocity = state
    
    # 密度の簡易モデル（高度による変化を無視）
    rho = 1.225
    
    # 揚力
    lift = 0.5 * lift_coefficient * rho * velocity**2
    
    # 重力
    weight = mass * gravity
    
    # 抗力
    drag = 0.5 * drag_coefficient * rho * velocity**2
    
    # 上昇力
    lift_force = lift - weight
    
    # 加速度
    acceleration = (thrust - drag) / mass
    
    return [velocity, acceleration]

# パラメータの設定
thrust = 50000  # 推力（N）
drag_coefficient = 0.3  # 抗力係数
lift_coefficient = 0.4  # 揚力係数
mass = 5000  # 航空機の質量（kg）
gravity = 9.81  # 重力加速度（m/s^2）

# 初期条件
initial_altitude = 0  # 初期高度（m）
initial_velocity = 0  # 初期速度（m/s）
initial_state = [initial_altitude, initial_velocity]

# 時間の範囲
t = np.linspace(0, 100, 1000)

# 運動方程式を解く
result = odeint(aircraft_motion_equation, initial_state, t, args=(thrust, drag_coefficient, lift_coefficient, mass, gravity))
altitude, velocity = result.T

# グラフのプロット
plt.plot(t, altitude, label='Altitude')
plt.plot(t, velocity, label='Velocity')
plt.xlabel('Time (s)')
plt.ylabel('Altitude (m) / Velocity (m/s)')
plt.title('Aircraft Motion')
plt.legend()
plt.grid(True)
plt.show()

このコードは、航空機の運動方程式を解き、時間に対する高度と速度の変化をグラフ化しています。

航空機の上昇および降下の動力学を簡単にモデル化することができます。

[実行結果]

ソースコード解説

このソースコードは、航空機の運動方程式を解いて結果をグラフ化するPythonプログラムです。

以下にコードの詳細な説明を示します。

1. ライブラリのインポート

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

numpy：数値計算を行うためのライブラリ
matplotlib.pyplot：グラフのプロットに使用するライブラリ
scipy.integrate.odeint：微分方程式を解くための関数

2. 航空機の運動方程式の定義

def aircraft_motion_equation(state, t, thrust, drag_coefficient, lift_coefficient, mass, gravity):
    # 状態変数
    altitude, velocity = state
    
    # 密度の簡易モデル（高度による変化を無視）
    rho = 1.225
    
    # 揚力
    lift = 0.5 * lift_coefficient * rho * velocity**2
    
    # 重力
    weight = mass * gravity
    
    # 抗力
    drag = 0.5 * drag_coefficient * rho * velocity**2
    
    # 上昇力
    lift_force = lift - weight
    
    # 加速度
    acceleration = (thrust - drag) / mass
    
    return [velocity, acceleration]

航空機の運動方程式を表す関数です。
引数として状態変数 state、時間 t、航空機のパラメータ（推力、抗力係数、揚力係数、質量、重力加速度）を取ります。
関数内で、高度と速度から揚力、重力、抗力を計算し、運動方程式に基づいて加速度を計算します。
計算結果として、速度と加速度のリストを返します。

3. パラメータの設定

thrust = 50000  # 推力（N）
drag_coefficient = 0.3  # 抗力係数
lift_coefficient = 0.4  # 揚力係数
mass = 5000  # 航空機の質量（kg）
gravity = 9.81  # 重力加速度（m/s^2）

航空機のパラメータを設定します。

推力、抗力係数、揚力係数、航空機の質量、重力加速度が含まれます。

4. 初期条件の設定

1
2
3

initial_altitude = 0  # 初期高度（m）
initial_velocity = 0  # 初期速度（m/s）
initial_state = [initial_altitude, initial_velocity]

初期高度と初期速度を設定し、状態変数の初期値としてリストに格納します。

5. 時間の範囲の設定

1	t = np.linspace(0, 100, 1000)

時間の範囲を設定します。
ここでは$0$から$100$までの範囲を等間隔で$1000$分割しています。

6. 運動方程式の解析

1 2	result = odeint(aircraft_motion_equation, initial_state, t, args=(thrust, drag_coefficient, lift_coefficient, mass, gravity)) altitude, velocity = result.T

odeint を使用して、航空機の運動方程式を解析します。
初期状態、時間、およびパラメータを引数として渡します。
解析結果から高度と速度を取得します。

7. グラフのプロット

plt.plot(t, altitude, label='Altitude')
plt.plot(t, velocity, label='Velocity')
plt.xlabel('Time (s)')
plt.ylabel('Altitude (m) / Velocity (m/s)')
plt.title('Aircraft Motion')
plt.legend()
plt.grid(True)
plt.show()

matplotlib.pyplot を使用して、時間に対する高度と速度の変化をプロットします。
$X軸$に時間（秒）、$Y軸$に高度（メートル）と速度（メートル/秒）を表示します。
グラフのタイトルやラベルを設定し、凡例とグリッドを追加しています。

結果解説

[実行結果]

上記のコードで生成されるグラフには、時間と高度、速度の関係が表示されます。

横軸は時間（秒）を表し、縦軸には高度（メートル）と速度（メートル/秒）が表示されます。
「Altitude」という線は、航空機の高度の変化を示しています。
航空機の高度が時間とともにどのように変化するかを示しています。
「Velocity」という線は、航空機の速度の変化を示しています。
航空機の速度が時間とともにどのように変化するかを示しています。

グラフの挙動を詳しく説明すると：

初期状態では、高度と速度はともにゼロです。
時間が経つにつれて、航空機の推力が働くことで高度が上昇し、速度が増加します。
一定の高度に達した後、航空機は水平飛行に移行し、高度は一定になりますが、速度は一定にはなりません。
速度は、推力と抗力のバランスによって決まります。
最終的に、航空機が安定した速度に達し、高度も一定になります。

このように、グラフは航空機の運動を時間とともに可視化しています。

感染症の伝播（SIRモデル）

2月 15, 2024

感染症の伝播（SIRモデル）

病気に関する方程式の例として、感染症の伝播を表すSIRモデルを取り上げます。

このモデルは、人口を感受性（S）、感染（I）、回復（R）の3つのカテゴリに分類し、これらのカテゴリ間で移行が起こると仮定します。

SIRモデルの方程式は以下の通りです：

$$
\frac{dS}{dt} = -\frac{\beta SI}{N}
$$

$$
\frac{dI}{dt} = \frac{\beta SI}{N} - \gamma I
$$

$$
\frac{dR}{dt} = \gamma I
$$

ここで、$ (S) $は感受性保持者の数、$ (I) $は感染者の数、$ (R) $は回復者の数、$ (N) $は総人口の数、$ (\beta) $は感染率、$ (\gamma) $は回復率です。

Pythonを使用してこのモデルを解き、グラフ化するコードは以下のようになります。

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# SIRモデルの微分方程式
def sir_model(y, t, beta, gamma, N):
    S, I, R = y
    dSdt = -beta * S * I / N
    dIdt = beta * S * I / N - gamma * I
    dRdt = gamma * I
    return [dSdt, dIdt, dRdt]

# 初期値
N = 1000  # 総人口
I0 = 1    # 初期感染者数
R0 = 0    # 初期回復者数
S0 = N - I0 - R0  # 初期感受性保持者数
beta = 0.3  # 感染率
gamma = 0.1  # 回復率

# 時間の設定
t = np.linspace(0, 160, 160)

# SIRモデルを解く
solution = odeint(sir_model, [S0, I0, R0], t, args=(beta, gamma, N))
S, I, R = solution.T

# グラフ化
plt.figure(figsize=(10, 6))
plt.plot(t, S, label='Susceptible')
plt.plot(t, I, label='Infected')
plt.plot(t, R, label='Recovered')
plt.xlabel('Time (days)')
plt.ylabel('Population')
plt.title('SIR Model')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、初期の感染者数と回復者数を設定し、微分方程式を解いて各カテゴリの人数を求め、それをグラフ化しています。

[実行結果]

ソースコード解説

このソースコードは、感染症の伝播をモデル化するSIRモデルを使用しています。

以下はソースコードの章立て詳細な説明です：

1. ライブラリのインポート:

import numpy as np:
数値計算を行うためのライブラリであるNumPyをインポートします。
これにより、配列操作や数学的な計算が可能になります。
from scipy.integrate import odeint:
微分方程式を解くためのodeint関数をSciPyからインポートします。
import matplotlib.pyplot as plt:
データの可視化のためのMatplotlibをインポートします。

2. SIRモデルの微分方程式の定義:

def sir_model(y, t, beta, gamma, N):
SIRモデルの微分方程式を定義します。
この関数は、現在の状態$y$と時間$t$に対して微分方程式を解きます。
また、感染率（$beta$）、回復率（$gamma$）、総人口（$N$）のパラメータも受け取ります。

3. 初期値の設定:

初期感染者数（$I0$）、初期回復者数（$R0$）などの各種パラメータが設定されています。

4. 時間の設定:

t = np.linspace(0, 160, 160):
$0$から$160$までの範囲を$160$個の点に分割して、時間の配列を作成します。
これにより、微分方程式が時間に沿って解かれます。

5. 微分方程式の解析:

solution = odeint(sir_model, [S0, I0, R0], t, args=(beta, gamma, N)):
odeint関数を使用してSIRモデルの微分方程式を解きます。
初期条件として、感受性保持者数（$S0$）、感染者数（$I0$）、回復者数（$R0$）を与え、時間t、感染率（$beta$）、回復率（$gamma$）、総人口（$N$）を引数として渡します。

6. グラフ化:

解析結果をプロットして、感受性保持者、感染者、回復者の人数の時間変化を可視化します。
それぞれのプロットは異なる色で示され、凡例にはそれぞれのカテゴリ名が表示されます。
plt.xlabel, plt.ylabel, plt.titleを使用して、軸ラベルやタイトルを追加します。
plt.legend()を使って凡例を表示し、plt.grid(True)でグリッド線を表示します。
plt.show()でグラフを表示します。

このコードは、SIRモデルを使って感染症の伝播を数値的に解析し、結果をグラフ化するものです。

結果解説

[実行結果]

このグラフは、SIRモデル（感受性(S)、感染(I)、回復(R)）に基づいて感染症の伝播をモデル化した結果を示しています。

時間軸 (Time):

グラフの横軸は時間を表し、単位は日数です。
感染の伝播が時間の経過とともにどのように変化するかを示します。

人口 (Population):

グラフの縦軸は人口を表します。
感受性保持者、感染者、回復者の数が表示されます。

感受性保持者 (Susceptible):

曲線”Susceptible”は感受性保持者の数を示します。
つまり、まだ感染していない人々の数です。
感染者との接触によって感染のリスクにさらされています。

感染者 (Infected):

曲線”Infected”は感染者の数を示します。
感染者は他の人々に病気を伝染させる可能性があります。
感染者の数が増えると、感染が拡大していることを示します。

回復者 (Recovered):

曲線”Recovered”は回復者の数を示します。
回復者は感染から回復し、免疫を獲得した人々です。
回復者の数が増えると、感染の広がりが鈍化し、感染者数が減少することを示します。

ピーク (Peak):

“Infected”曲線の頂点が感染のピークを表します。
ピーク時に感染者数が最大となり、その後減少し始めます。

このグラフを通じて、感染症の伝播パターンや感染のピーク時期、回復の進行など、感染症の伝播プロセスに関する情報が視覚的に理解できます。

天気に関する方程式

2月 14, 2024

天気に関する方程式

天気に関する方程式の例として、気温の変化を表す単純なモデルを考えてみましょう。

例えば、一日の時間による気温の変化をモデル化することができます。

$$
T(t) = A \sin(\omega t + \phi) + C
$$

ここで、$ ( T(t) ) $は時間$ ( t ) $における気温を表し、$ ( A ) $は振幅、$ ( \omega ) $は角周波数、$ ( \phi ) $は位相差、$ ( C ) $は平均気温を表します。

これをPythonで解いてグラフ化してみましょう。

import numpy as np
import matplotlib.pyplot as plt

# パラメータの設定
A = 10  # 振幅 (℃)
omega = 2 * np.pi / 24  # 角周波数 (1時間あたりのラジアン)
phi = 0  # 位相差
C = 20  # 平均気温 (℃)

# 時間の範囲を設定
t_values = np.linspace(0, 24, 100)  # 0時から24時までの範囲を100分割

# 気温の計算
T_values = A * np.sin(omega * t_values + phi) + C

# グラフの描画
plt.plot(t_values, T_values)
plt.title('Daily Temperature Variation')
plt.xlabel('Time (hours)')
plt.ylabel('Temperature (°C)')
plt.grid(True)
plt.show()

このコードでは、一日の時間に応じた気温の変化を示すグラフを描画しています。

[実行結果]

振幅、角周波数、位相差、平均気温などのパラメータを調整することで、異なる天候パターンに対応するグラフを作成できます。

ソースコード解説

このソースコードは、一日の時間に対する気温の変化をモデル化し、それをグラフ化するものです。

以下は、コードの詳細な説明です。

1. ライブラリのインポート:

1 2	import numpy as np import matplotlib.pyplot as plt

numpy パッケージは数値計算を行うためのパッケージであり、配列や数学的な関数を提供します。
matplotlib.pyplot モジュールは、データの可視化を行うためのライブラリであり、グラフを描画する際に使用されます。

2. パラメータの設定:

A = 10  # 振幅 (℃)
omega = 2 * np.pi / 24  # 角周波数 (1時間あたりのラジアン)
phi = 0  # 位相差
C = 20  # 平均気温 (℃)

A は振幅であり、気温の変化の大きさを表します。
omega は角周波数であり、1時間あたりのラジアンで表されます。
ここでは、一日の周期を考慮しています。
phi は位相差であり、波形の位相を調整します。
ここでは、$0$としています。
C は平均気温であり、波形の水平方向のシフトを表します。

3. 時間の範囲の設定:

1	t_values = np.linspace(0, 24, 100) # 0時から24時までの範囲を100分割

np.linspace() 関数を使用して、$0$から$24$までの範囲を$100$分割した時間の配列を作成します。

4. 気温の計算:

1	T_values = A * np.sin(omega * t_values + phi) + C

時間に対する気温の変化を計算します。
ここでは、振幅と角周波数を用いた正弦関数を使っています。
また、位相差と平均気温を加えています。

5. グラフの描画:

plt.plot(t_values, T_values)
plt.title('Daily Temperature Variation')
plt.xlabel('Time (hours)')
plt.ylabel('Temperature (°C)')
plt.grid(True)
plt.show()

plt.plot() 関数を使用して、時間に対する気温の変化を描画します。
plt.title()、plt.xlabel()、plt.ylabel() 関数を使用して、タイトルや軸ラベルを設定します。
plt.grid(True) は、グリッドを表示するための命令です。
最後の plt.show() は、グラフを表示します。

結果解説

[実行結果]

このグラフは、一日の時間に対する気温の変化を表しています。

以下は、グラフの各要素の詳細です：

X軸 (Time)：

一日の時間を表します。
単位は時間です。
この軸は、24時間を通じて時間の経過に対する変化を示します。

Y軸 (Temperature)：

気温を表します。
単位は摂氏 (℃) です。この軸は、気温の変化を示します。

グラフの線：

$X$軸の値 (時間) に対する、$Y$軸の値 (気温) を表す曲線です。
この曲線は、一日の時間に応じて気温がどのように変化するかを示しています。
振幅、角周波数、位相差、平均気温などのパラメータによって、この曲線の形状が変化します。

グリッド：

背景に表示される格子状の線で、データの視覚的な評価を支援します。
水平方向と垂直方向の線が交わる点で、それぞれの時間と気温の値が示されます。

このグラフからは、一日の時間帯によって気温が変化する様子がわかります。

クーロンの法則

2月 13, 2024

クーロンの法則

クーロンの法則は、電荷間の相互作用を記述する法則であり、以下の式で表されます：

$$
F = \frac{k \cdot q_1 \cdot q_2}{r^2}
$$

ここで、$ ( F ) $は電荷間の力、$ ( k ) $はクーロン定数 $ (( 8.9875 \times 10^9 , \text{N m}^2/\text{C}^2 )）$、$ ( q_1 ) $と$ ( q_2 ) $はそれぞれの電荷、$ ( r ) $は電荷間の距離です。

これを Python で解いて、結果をグラフ化してみましょう。

import numpy as np
import matplotlib.pyplot as plt

# クーロンの法則
def coulombs_law(q1, q2, r):
    k = 8.9875e9  # クーロン定数 (N m^2 / C^2)
    return k * q1 * q2 / r**2

# 電荷の設定
q1 = 1e-6  # 電荷1 (C)
q2 = -1e-6  # 電荷2 (C)

# 距離の範囲
r_values = np.linspace(1, 10, 100)  # 1 から 10 の範囲で距離を設定

# 電荷間の力を計算
force_values = coulombs_law(q1, q2, r_values)

# グラフ化
plt.plot(r_values, force_values)
plt.title("Coulomb's Law")
plt.xlabel('Distance (m)')
plt.ylabel('Force (N)')
plt.grid(True)
plt.show()

このコードは、クーロンの法則を用いて電荷間の力を計算し、結果をグラフ化します。

[実行結果]

ソースコード解説

以下は、ソースコードの詳細な説明です。

ライブラリのインポート:

1 2	import numpy as np import matplotlib.pyplot as plt

numpy は数値計算を行うためのパッケージです。
主に配列や行列などの数学的な演算をサポートします。
matplotlib.pyplot はデータを可視化するためのライブラリです。
グラフや図を描画する際に使用されます。

クーロンの法則を定義する関数:

1
2
3

def coulombs_law(q1, q2, r):
    k = 8.9875e9  # クーロン定数 (N m^2 / C^2)
    return k * q1 * q2 / r**2

coulombs_law 関数は、クーロンの法則に基づいて電荷間の力を計算します。
q1 と q2 はそれぞれの電荷の大きさを表し、r は電荷間の距離です。
k はクーロン定数であり、$ (8.9875 \times 10^9 , \text{N m}^2/\text{C}^2) $で定義されています。

電荷の設定:

1 2	q1 = 1e-6 # 電荷1 (C) q2 = -1e-6 # 電荷2 (C)

q1 と q2 は、それぞれの電荷の大きさを表す変数です。
ここでは、$ 1e-6 $ C (クーロン) と$ -1e-6 $ Cの電荷を設定しています。

距離の範囲の設定:

1	r_values = np.linspace(1, 10, 100) # 1 から 10 の範囲で距離を設定

np.linspace 関数を使用して、$ 1 $から$ 10 $の範囲で距離を等間隔で$100$点取得しています。

電荷間の力の計算:

1	force_values = coulombs_law(q1, q2, r_values)

先ほど定義した coulombs_law 関数を使用して、電荷間の距離に応じた力を計算しています。

グラフの作成と表示:

plt.plot(r_values, force_values)
plt.title("Coulomb's Law")
plt.xlabel('Distance (m)')
plt.ylabel('Force (N)')
plt.grid(True)
plt.show()

plt.plot 関数を使用して、距離に対する力のグラフを描画します。
plt.title、plt.xlabel、plt.ylabel 関数を使用して、タイトルや軸ラベルを設定します。
plt.grid(True) は、グリッドを表示するための命令です。
最後の plt.show() は、グラフを表示します。

結果解説

[実行結果]

このグラフは、クーロンの法則に基づいて計算された電荷間の力を距離に対してプロットしたものです。

以下はグラフの各要素の詳細です：

$X$軸 (Distance)：

電荷間の距離を表します。
単位はメートル (m) です。
この軸は、電荷同士の間隔がどのように変化するかを示しています。

$Y$軸 (Force)：

電荷間の力を表します。
単位はニュートン (N) です。
この軸は、電荷同士の間に生じる相互作用力がどのように変化するかを示しています。

グラフの線：

$X$軸の値 (距離) に対する、$Y$軸の値 (力) を表す曲線です。
クーロンの法則に従って、電荷間の距離が近づくにつれて力が増加し、距離が離れるにつれて力が減少することが期待されます。

グリッド：

背景に表示される格子状の線で、データの視覚的な評価を支援します。
水平方向と垂直方向の線が交わる点で、それぞれの距離と力の値が示されます。

このグラフからは、電荷間の力が距離の関数としてどのように振る舞うかがわかります。

距離が増加するにつれて、力が減少することが確認できます。

この振る舞いは、クーロンの法則の特徴的な振る舞いを示しています。

球面方程式

2月 12, 2024

球面方程式

３次元方程式の例としては、例えば球面方程式が挙げられます。

球面方程式は以下のように表されます:

$$
x^2 + y^2 + z^2 = r^2
$$

ここで、$ ( r ) $は球の半径です。

以下に、Pythonでこの球面方程式を解いてグラフ化するコードを示します。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# Sphere equation parameters
r = 1  # Radius

# Generate points on the sphere
theta = np.linspace(0, 2 * np.pi, 100)
phi = np.linspace(0, np.pi, 100)
x = r * np.outer(np.cos(theta), np.sin(phi))
y = r * np.outer(np.sin(theta), np.sin(phi))
z = r * np.outer(np.ones(100), np.cos(phi))

# Plot
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, color='b', alpha=0.5)

# Set equal aspect ratio
ax.set_box_aspect([1,1,1])

# Set labels
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.title('Sphere')

plt.show()

このコードは、半径が$1$の球を描画しています。

[実行結果]

必要に応じて、r の値を変更して異なる半径の球を描画することができます。

ソースコード解説

このソースコードは、Pythonで半径が$1$の球面を描画するためのプログラムです。

以下はそれぞれの部分の詳細な説明です。

ライブラリのインポートとモジュールの選択

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

numpyは、数値計算を行うためのPythonのライブラリです。
主に多次元配列や行列演算、数学関数などを提供します。
matplotlib.pyplotは、グラフ描画のためのライブラリです。
主に2次元のグラフを描画するための機能を提供します。
mpl_toolkits.mplot3dは、3次元のグラフ描画のためのツールキットです。
これには、3Dプロットを作成するための機能が含まれています。

球面方程式のパラメータの設定

1	r = 1 # Radius

rは球の半径を表します。
この場合、半径は$1$と設定されています。

球面上の点の生成

theta = np.linspace(0, 2 * np.pi, 100)
phi = np.linspace(0, np.pi, 100)
x = r * np.outer(np.cos(theta), np.sin(phi))
y = r * np.outer(np.sin(theta), np.sin(phi))
z = r * np.outer(np.ones(100), np.cos(phi))

thetaとphiはそれぞれ、水平方向と垂直方向の角度を表します。
np.linspaceは、指定された範囲内で等間隔の値を生成します。
np.outerは、2つのベクトルの外積を計算します。
ここでは、球面上の点の座標を計算するために使用されます。
x、y、zは、それぞれ球面上の点の$x$座標、$y$座標、$z$座標を表します。

グラフの描画

1
2
3

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, color='b', alpha=0.5)

plt.figure()は、新しい図を作成します。
fig.add_subplot(111, projection='3d')は、3Dプロット用のサブプロットを作成します。
ax.plot_surface(x, y, z, color='b', alpha=0.5)は、球面を描画します。
x、y、zは、それぞれ球面上の点の座標を表し、colorは色を指定します。
alphaは透明度を設定します。

グラフの設定

ax.set_box_aspect([1,1,1])
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.title('Sphere')

ax.set_box_aspect([1,1,1])は、3Dプロットの表示を正確なアスペクト比で設定します。
ax.set_xlabel('X')、ax.set_ylabel('Y')、ax.set_zlabel('Z')は、それぞれ$X$軸、$Y$軸、$Z$軸のラベルを設定します。
plt.title('Sphere')は、グラフのタイトルを設定します。

グラフの表示

1	plt.show()

plt.show()は、プロットを表示します。

これらの手順が組み合わさって、半径が$1$の球面が3Dグラフ上に描画されます。

結果解説

[実行結果]

以下はグラフに表示される内容の詳細です:

1. 3次元座標系:

グラフ上には、$X$軸、$Y$軸、$Z$軸があります。
これらはそれぞれ球の中心を通る直線です。

2. 球面:

グラフ上には、半径が$1$の球面が描かれます。
球面は、球の中心を中心として座標系の全方向に等しく広がっています。
球面は青色で描かれ、半透明になっています。

3. 等距離線:

球面上の等距離線は、球の中心から球面上の各点までの距離が等しい点の集合を示しています。
これは球面が円状の断面を持つことを視覚的に示しています。

4. プロットの表示:

3Dグラフでは、各軸上の値に対応する点がプロットされます。
この例では、球面上の多くの点がプロットされていますが、それらの点が球面上にあることが示されています。

5. タイトルと軸ラベル:

グラフには、「Sphere」というタイトルが表示され、各軸には「X」、「Y」、「Z」というラベルが付けられています。
これらのラベルは、それぞれ$X$軸、$Y$軸、$Z$軸を表します。

これらの要素が組み合わさって、3次元空間内で半径が$1$の球面が視覚化されます。

プラズマのエネルギー収支方程式

2月 11, 2024

プラズマのエネルギー収支方程式

核融合に関する基本的な方程式として、例えばプラズマのエネルギー収支方程式があります。

これはプラズマ内でのエネルギーの生成と損失を表します。

ここでは、プラズマのエネルギー収支方程式を簡単なモデルで表現し、Pythonで解いてグラフ化する方法を示します。

以下の例では、プラズマ内のエネルギー生成と損失を表す関数を定義し、微分方程式を解いて時間変化をプロットします。

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

# プラズマのエネルギー収支方程式の定義
def plasma_energy_balance(t, E):
    # パラメータ
    alpha = 1.0  # エネルギー生成率
    beta = 0.5   # エネルギー損失率

    # エネルギーの時間変化
    dEdt = alpha - beta * E

    return dEdt

# 初期エネルギー
E0 = 0.0

# 時間範囲
t_span = (0, 10)  # 0から10までの時間

# 時間点
t_eval = np.linspace(0, 10, 100)

# 常微分方程式の解く
sol = solve_ivp(plasma_energy_balance, t_span, [E0], t_eval=t_eval)

# 結果のグラフ化
plt.figure(figsize=(10, 6))
plt.plot(sol.t, sol.y[0], label='Plasma Energy')
plt.xlabel('Time')
plt.ylabel('Energy')
plt.title('Plasma Energy Balance')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、プラズマのエネルギー収支方程式を定義し、SciPyのsolve_ivp関数を使用してこの微分方程式を解いています。

そして、プラズマのエネルギーが時間とともにどのように変化するかをグラフ化しています。

[実行結果]

ソースコード解説

以下にソースコード詳細な説明を示します。

ライブラリのインポート

1
2
3

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

numpy：数値計算を行うための基本的なライブラリ。
scipy.integrate.solve_ivp：常微分方程式を解くための関数を提供するSciPyのモジュール。
matplotlib.pyplot：データの可視化を行うためのグラフ描画ライブラリ。

プラズマのエネルギー収支方程式の定義

def plasma_energy_balance(t, E):
    # パラメータ
    alpha = 1.0  # エネルギー生成率
    beta = 0.5   # エネルギー損失率

    # エネルギーの時間変化
    dEdt = alpha - beta * E

    return dEdt

plasma_energy_balance 関数：プラズマのエネルギー収支方程式を定義します。
この関数は、時間 t と現在のエネルギー E を受け取り、時間変化率 dEdt を計算して返します。

初期エネルギーの設定

E0 = 0.0

E0：初期のプラズマのエネルギーを設定します。

時間範囲の設定

1	t_span = (0, 10) # 0から10までの時間

t_span：解析する時間範囲を設定します。
ここでは、$0$から$10$までの時間を指定しています。

時間点の設定

1	t_eval = np.linspace(0, 10, 100)

t_eval：グラフ化する際の時間点を設定します。
ここでは、$0$から$10$までの時間を$100$等分した時間点を指定しています。

常微分方程式の解く

1	sol = solve_ivp(plasma_energy_balance, t_span, [E0], t_eval=t_eval)

solve_ivp 関数：プラズマのエネルギー収支方程式を解きます。
初期エネルギー E0 から始まり、t_span の時間範囲で解析し、t_eval で指定された時間点で解を計算します。

結果のグラフ化

plt.figure(figsize=(10, 6))
plt.plot(sol.t, sol.y[0], label='Plasma Energy')
plt.xlabel('Time')
plt.ylabel('Energy')
plt.title('Plasma Energy Balance')
plt.legend()
plt.grid(True)
plt.show()

プロットの設定：グラフのサイズ、ラベル、タイトル、凡例などを設定します。
plt.plot：解析結果をグラフにプロットします。
横軸に時間、縦軸にプラズマのエネルギーを設定し、ラベルを付けています。
plt.show：グラフを表示します。

これにより、プラズマのエネルギー収支方程式を解いて時間変化をグラフ化する完全なプロセスが実行されます。

結果解説

[実行結果]

このグラフは、時間に対するプラズマのエネルギーの変化を示しています。

横軸は時間を表し、縦軸はプラズマのエネルギーを表します。
グラフ上の曲線は、時間とともにプラズマのエネルギーがどのように変化するかを表します。
最初の時点では、初期エネルギーが$0$であるため、グラフの始点は原点になります。
曲線の傾きは、プラズマのエネルギーの時間変化率を示しており、この例では定数の生成率と損失率に基づいています。
時間が経過するにつれて、エネルギー生成と損失の影響により、プラズマのエネルギーが変化します。
グラフ全体の形状は、生成率と損失率によって異なります。
生成率が損失率よりも大きい場合、エネルギーは増加し続ける傾向がありますが、逆の場合はエネルギーが減少します。
グラフが時間の経過とともにどのように振る舞うかは、定義したエネルギー収支方程式に基づいています。

このようなグラフを通じて、時間に対するプラズマのエネルギーの挙動を直感的に理解することができます。