感染症の伝播（SIRモデル）

感染症の伝播（SIRモデル）

病気に関する方程式の例として、感染症の伝播を表すSIRモデルを取り上げます。

このモデルは、人口を感受性（S）、感染（I）、回復（R）の3つのカテゴリに分類し、これらのカテゴリ間で移行が起こると仮定します。

SIRモデルの方程式は以下の通りです：

$$
\frac{dS}{dt} = -\frac{\beta SI}{N}
$$

$$
\frac{dI}{dt} = \frac{\beta SI}{N} - \gamma I
$$

$$
\frac{dR}{dt} = \gamma I
$$

ここで、$ (S) $は感受性保持者の数、$ (I) $は感染者の数、$ (R) $は回復者の数、$ (N) $は総人口の数、$ (\beta) $は感染率、$ (\gamma) $は回復率です。

Pythonを使用してこのモデルを解き、グラフ化するコードは以下のようになります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# SIRモデルの微分方程式
def sir_model(y, t, beta, gamma, N):
    S, I, R = y
    dSdt = -beta * S * I / N
    dIdt = beta * S * I / N - gamma * I
    dRdt = gamma * I
    return [dSdt, dIdt, dRdt]

# 初期値
N = 1000  # 総人口
I0 = 1    # 初期感染者数
R0 = 0    # 初期回復者数
S0 = N - I0 - R0  # 初期感受性保持者数
beta = 0.3  # 感染率
gamma = 0.1  # 回復率

# 時間の設定
t = np.linspace(0, 160, 160)

# SIRモデルを解く
solution = odeint(sir_model, [S0, I0, R0], t, args=(beta, gamma, N))
S, I, R = solution.T

# グラフ化
plt.figure(figsize=(10, 6))
plt.plot(t, S, label='Susceptible')
plt.plot(t, I, label='Infected')
plt.plot(t, R, label='Recovered')
plt.xlabel('Time (days)')
plt.ylabel('Population')
plt.title('SIR Model')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、初期の感染者数と回復者数を設定し、微分方程式を解いて各カテゴリの人数を求め、それをグラフ化しています。

[実行結果]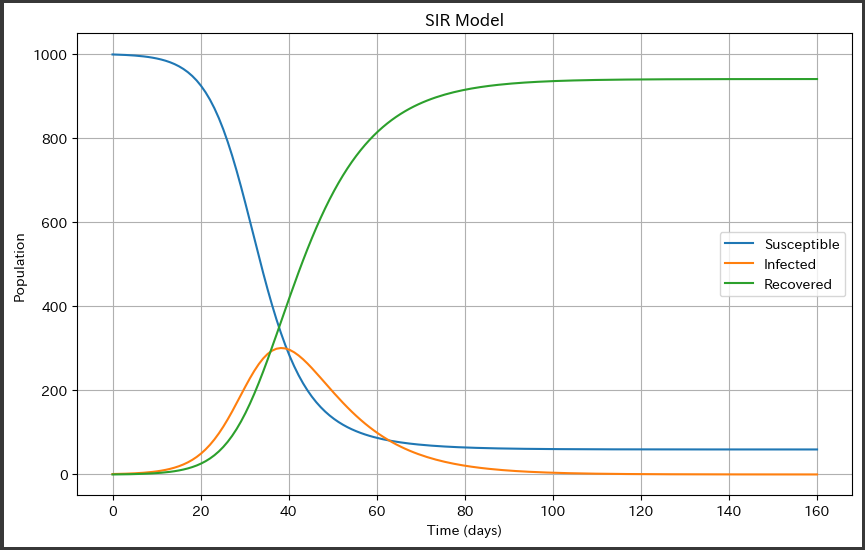

ソースコード解説

このソースコードは、感染症の伝播をモデル化するSIRモデルを使用しています。

以下はソースコードの章立て詳細な説明です：

1. ライブラリのインポート:

  • import numpy as np:
    数値計算を行うためのライブラリであるNumPyをインポートします。
    これにより、配列操作や数学的な計算が可能になります。
  • from scipy.integrate import odeint:
    微分方程式を解くためのodeint関数をSciPyからインポートします。
  • import matplotlib.pyplot as plt:
    データの可視化のためのMatplotlibをインポートします。

2. SIRモデルの微分方程式の定義:

  • def sir_model(y, t, beta, gamma, N):
    SIRモデルの微分方程式を定義します。
    この関数は、現在の状態$y$と時間$t$に対して微分方程式を解きます。
    また、感染率（$beta$）、回復率（$gamma$）、総人口（$N$）のパラメータも受け取ります。

3. 初期値の設定:

  • 初期感染者数（$I0$）、初期回復者数（$R0$）などの各種パラメータが設定されています。

4. 時間の設定:

  • t = np.linspace(0, 160, 160):
    $0$から$160$までの範囲を$160$個の点に分割して、時間の配列を作成します。
    これにより、微分方程式が時間に沿って解かれます。

5. 微分方程式の解析:

  • solution = odeint(sir_model, [S0, I0, R0], t, args=(beta, gamma, N)):
    odeint関数を使用してSIRモデルの微分方程式を解きます。
    初期条件として、感受性保持者数（$S0$）、感染者数（$I0$）、回復者数（$R0$）を与え、時間t、感染率（$beta$）、回復率（$gamma$）、総人口（$N$）を引数として渡します。

6. グラフ化:

  • 解析結果をプロットして、感受性保持者、感染者、回復者の人数の時間変化を可視化します。
    それぞれのプロットは異なる色で示され、凡例にはそれぞれのカテゴリ名が表示されます。
  • plt.xlabel, plt.ylabel, plt.titleを使用して、軸ラベルやタイトルを追加します。
  • plt.legend()を使って凡例を表示し、plt.grid(True)でグリッド線を表示します。
  • plt.show()でグラフを表示します。

このコードは、SIRモデルを使って感染症の伝播を数値的に解析し、結果をグラフ化するものです。

結果解説

[実行結果]

このグラフは、SIRモデル（感受性(S)、感染(I)、回復(R)）に基づいて感染症の伝播をモデル化した結果を示しています。

時間軸 (Time):

グラフの横軸は時間を表し、単位は日数です。
感染の伝播が時間の経過とともにどのように変化するかを示します。

人口 (Population):

グラフの縦軸は人口を表します。
感受性保持者、感染者、回復者の数が表示されます。

感受性保持者 (Susceptible):

曲線”Susceptible”は感受性保持者の数を示します。
つまり、まだ感染していない人々の数です。
感染者との接触によって感染のリスクにさらされています。

感染者 (Infected):

曲線”Infected”は感染者の数を示します。
感染者は他の人々に病気を伝染させる可能性があります。
感染者の数が増えると、感染が拡大していることを示します。

回復者 (Recovered):

曲線”Recovered”は回復者の数を示します。
回復者は感染から回復し、免疫を獲得した人々です。
回復者の数が増えると、感染の広がりが鈍化し、感染者数が減少することを示します。

ピーク (Peak):

“Infected”曲線の頂点が感染のピークを表します。
ピーク時に感染者数が最大となり、その後減少し始めます。

このグラフを通じて、感染症の伝播パターンや感染のピーク時期、回復の進行など、感染症の伝播プロセスに関する情報が視覚的に理解できます。