オイラー法

数理解析の例題として、オイラー法による2階常微分方程式の解法をPythonで解き、グラフ化することを考えます。

この問題は、物理的シミュレーションや工学の問題など、様々な分野で使用されます。

まず、オイラー法による2階常微分方程式の解法について説明します。
オイラー法は、微分方程式を数値的に解くための方法で、特に時間に依存する物理現象を模擬する際によく使用されます。
この方法では、微分方程式を一連の一階の微分方程式に変換し、それぞれを個別に解いていきます

Pythonでこの問題を解くためには、以下の手順を踏むことになります。

  1. 時間の上限$T$と時間刻み幅$h$を定義します。
  2. 解を保存するための配列$y1[N+1]$,$ y2[N+1]$,$ t[N+1]$を用意します。
  3. 微分方程式を満たす関数$f1(t,y1,y2)$, $f2(t,y1,y2)$を定義します。
  4. 初期条件$y1[0] = a1$,$ y2[0] = a2$, $t[0] = 0$を設定します。
  5. 時間刻み幅$h$で時間tを進めながら、各時点での解を計算し、配列に保存します。
  6. 最後に、matplotlibを使用して計算結果をグラフ化します

以下に、これらの手順を実装したPythonコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import matplotlib.pyplot as plt

# 定数と初期条件を設定
T = 10
h = 0.01
a1 = 1
a2 = 0

# 配列を用意
y1 = np.zeros(int(T/h)+1)
y2 = np.zeros(int(T/h)+1)
t = np.zeros(int(T/h)+1)

# 微分方程式を満たす関数を定義
def f1(t, y1, y2):
    return y2

def f2(t, y1, y2):
    return -y1

# 初期条件を設定
y1[0] = a1
y2[0] = a2
t[0] = 0

# 時間を進めながら解を計算
for j in range(1, int(T/h)+1):
    t[j] = j*h
    y1[j] = y1[j-1] + h*f1(t[j-1], y1[j-1], y2[j-1])
    y2[j] = y2[j-1] + h*f2(t[j-1], y1[j-1], y2[j-1])

# 結果をグラフ化
plt.figure()
plt.plot(t, y1, label='y1')
plt.plot(t, y2, label='y2')
plt.legend()
plt.show()

このコードは、オイラー法を用いて2階常微分方程式を解き、結果をグラフ化するものです。

微分方程式の形式や初期条件、時間の上限$T$、時間刻み幅$h$は任意に変更することができます。

[実行結果]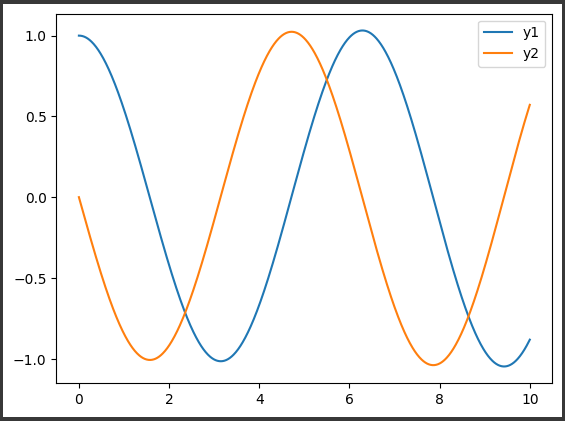

ソースコード解説

このソースコードは、2つの連立常微分方程式を数値的に解いてその解をグラフにプロットするプログラムです。

以下にプログラムの詳細な説明を示します：

1. ライブラリのインポート

1
2
import numpy as np
import matplotlib.pyplot as plt
  • NumPyとMatplotlibをインポートしています。
    NumPyは数値計算のためのライブラリであり、Matplotlibはグラフ描画のためのライブラリです。

2. 定数と初期条件の設定

1
2
3
4
T = 10
h = 0.01
a1 = 1
a2 = 0
  • 解析のための定数や初期条件を設定しています。
    ここでは、解析する時間の範囲を表す$T$、時間の刻み幅を表す$h$、初期値$a1$と$a2$を設定しています。

3. 配列の準備

1
2
3
y1 = np.zeros(int(T/h)+1)
y2 = np.zeros(int(T/h)+1)
t = np.zeros(int(T/h)+1)
  • 計算結果を格納するための配列$ y1$,$ y2$,$ t $を用意しています。
    これらの配列は、時間の刻み幅$h$に基づいて計算される結果を保持します。

4. 微分方程式を満たす関数の定義

1
2
3
4
5
def f1(t, y1, y2):
    return y2

def f2(t, y1, y2):
    return -y1
  • 解きたい連立常微分方程式を満たす関数$ f1$, $f2 $を定義しています。
    この例では、1つ目の方程式が$dy1/dt = y2$、2つ目の方程式が$dy2/dt = -y1$に対応しています。

5. 初期条件の設定

1
2
3
y1[0] = a1
y2[0] = a2
t[0] = 0
  • 初期条件を配列に設定しています。

6. 時間を進めながら解を計算

1
2
3
4
for j in range(1, int(T/h)+1):
    t[j] = j*h
    y1[j] = y1[j-1] + h*f1(t[j-1], y1[j-1], y2[j-1])
    y2[j] = y2[j-1] + h*f2(t[j-1], y1[j-1], y2[j-1])
  • Eulerの方法を使用して、連立常微分方程式を数値的に解いています。
    時間を進めながら、前の時間ステップの解を使用して次の解を計算します。

7. 結果のグラフ化

1
2
3
4
5
plt.figure()
plt.plot(t, y1, label='y1')
plt.plot(t, y2, label='y2')
plt.legend()
plt.show()
  • 得られた解をMatplotlibを使用してグラフにプロットし、$y1$曲線と$y2$曲線を表示しています。
    $y1$曲線は青色で、$y2$曲線はオレンジ色で表されます。

結果解説

[実行結果]

このグラフは、2つの曲線で構成されています。

1. $ y1 $曲線:

この曲線は、時間に対する$ (y1) $の値を表しています。
最初は初期値$ (a1) $から始まり、時間とともに変化します。
曲線の形状は、微分方程式$ (\frac{dy1}{dt} = y2) $に基づいて決定されます。
$ (y2) $の値が変化すると、$ (y1) $の変化速度も変わります。

2. $ y2 $曲線:

この曲線は、時間に対する$ (y2) $の値を表しています。
同様に、初期値$ (a2) $から始まり、時間とともに変化します。
曲線の形状は、微分方程式$ (\frac{dy2}{dt} = -y1) $に基づいて決定されます。
$ (y1) $の値が変化すると、$ (y2) $の変化速度も変わります。

このグラフを通じて、2つの関数$ (y1) $と$ (y2) $が時間の経過とともにどのように振る舞うかを視覚的に理解できます。