連立微分方程式

2月 19, 2024

連立微分方程式

4次元方程式の例として、次の連立微分方程式を考えます。

$$
\frac{dx}{dt} = -y
$$
$$
\frac{dy}{dt} = x - z
$$
$$
\frac{dz}{dt} = y - w
$$
$$
\frac{dw}{dt} = z
$$

これは、$(x)$、$(y)$、$(z)$、$(w)$の4つの変数を持つ4次元方程式です。

それでは、この方程式をPythonで解いてグラフ化しましょう。

以下がコードです。

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

# 4次元微分方程式
def equations(t, y):
    x, y, z, w = y
    dxdt = -y
    dydt = x - z
    dzdt = y - w
    dwdt = z
    return [dxdt, dydt, dzdt, dwdt]

# 初期条件と時間の設定
t_span = (0, 20)
t_eval = np.linspace(*t_span, 1000)
y0 = [1, 0, 0, 0]

# 方程式を解く
sol = solve_ivp(equations, t_span, y0, t_eval=t_eval)

# 結果をプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(sol.y[0], sol.y[1], sol.y[2], label='Trajectory')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.legend()
plt.show()

このコードは、4次元微分方程式を解き、その解を3次元空間上の軌跡としてグラフにプロットします。

[実行結果]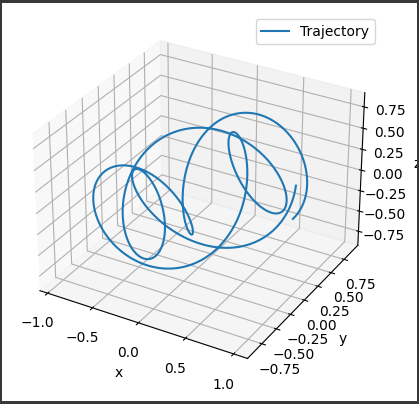

ソースコード解説

以下に、ソースコードの詳細な説明を示します。

1. ライブラリのインポート

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

NumPyは数値計算を行うためのライブラリ、Matplotlibはグラフ描画を行うためのライブラリ、scipy.integrateモジュールのsolve_ivp関数は常微分方程式を解くために使用されます。

2. 4次元微分方程式の定義

def equations(t, y):
    x, y, z, w = y
    dxdt = -y
    dydt = x - z
    dzdt = y - w
    dwdt = z
    return [dxdt, dydt, dzdt, dwdt]

equations関数では、4つの変数$ (x)$,$ (y)$,$ (z)$,$ (w) $に対する4次元微分方程式が定義されています。

3. 初期条件と時間の設定

1
2
3

t_span = (0, 20)
t_eval = np.linspace(*t_span, 1000)
y0 = [1, 0, 0, 0]

t_spanでは時間の範囲を指定し、t_evalではその範囲内で解を評価する時間の配列を生成します。
y0は初期条件を表し、この場合は$ (x = 1)$,$ (y = 0)$,$ (z = 0)$,$ (w = 0) $としています。

4. 方程式を解く

1	sol = solve_ivp(equations, t_span, y0, t_eval=t_eval)

solve_ivp関数を使用して微分方程式を解きます。
equations関数で定義された微分方程式、初期条件y0、評価する時間t_evalを引数として渡します。

5. 結果をプロット

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(sol.y[0], sol.y[1], sol.y[2], label='Trajectory')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.legend()
plt.show()

解析結果を3次元グラフにプロットします。
sol.yは解の配列で、sol.y[0]、sol.y[1]、sol.y[2]はそれぞれ$ (x)$、$(y)$、$(z)$の解を表します。

これを用いて3次元軌跡をプロットし、$x軸$、$y軸$、$z軸$にラベルを付けています。

結果解説

[実行結果]

このグラフは、4次元微分方程式の解を表す3次元の軌跡を示しています。

具体的には、$(x)$、$(y)$、$(z)$の3つの変数が時間に対してどのように変化するかを可視化しています。

$x軸$は変数$(x)$の値を表し、$y軸$は変数$(y)$の値を表します。
$z軸$は変数$(z)$の値を表しています。
しかし、実際には4次元方程式を解いているため、$(w)$変数の値が$z軸$に関連付けられます。
これは、3次元の空間で4次元方程式の解をプロットするための折衷案です。
軌跡は、初期条件から始まり、時間とともに変化する解の経路を示しています。
解の軌跡がどのように変化するかによって、4次元方程式の動的な振る舞いを視覚的に理解することができます。

このグラフは、4次元の微分方程式を解析する際に、解の性質や振る舞いを視覚化するのに役立ちます。