複利計算

2月 17, 2024

複利計算

投資に関する方程式の例として、単純な複利計算を考えてみましょう。

複利計算の方程式は以下のように表されます:

$$
A = P \times (1 + r)^n
$$

$ (A) $は最終的な金額（将来価値）
$ (P) $は元本（現在価値）
$ (r) $は年利率
$ (n) $は投資期間（年数）

これをPythonで解き、グラフ化する方法を示します。

import numpy as np
import matplotlib.pyplot as plt

def compound_interest(P, r, n):
    """
    複利計算を行う関数
    
    Parameters:
        P (float): 元本（現在価値）
        r (float): 年利率
        n (int): 投資期間（年数）
    
    Returns:
        np.ndarray: 各年の金額の配列
    """
    years = np.arange(1, n+1)
    A = P * (1 + r)**years
    return A

# パラメータの設定
P = 1000  # 元本
r = 0.05  # 年利率 (5%)
n = 10    # 投資期間（10年）

# 複利計算を実行
investment_values = compound_interest(P, r, n)

# グラフの描画
plt.plot(np.arange(1, n+1), investment_values, marker='o')
plt.title('Compound Interest over {} Years'.format(n))
plt.xlabel('Years')
plt.ylabel('Investment Value')
plt.grid(True)
plt.show()

このコードは、元本$ (P) $、年利率$ (r) $、投資期間$ (n) $を与えられたときに、各年の投資金額$ (A) $を計算し、それをグラフ化しています。

[実行結果]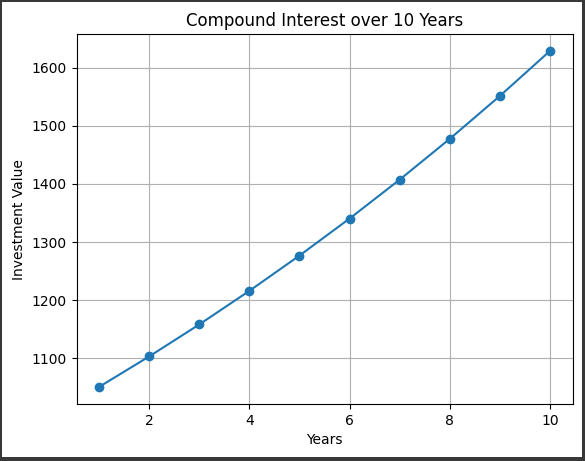

ソースコード解説

このソースコードは、Pythonを使用して複利計算を行い、その結果をグラフ化するプログラムです。

以下では、各部分の詳細を説明します。

ライブラリのインポート

1 2	import numpy as np import matplotlib.pyplot as plt

numpy は数値計算を行うためのライブラリです。
ここでは主に配列操作や数学的な計算に使用されます。
matplotlib.pyplot はグラフの描画に使用されるライブラリです。
plt として一般的にエイリアスされます。

複利計算の関数定義

def compound_interest(P, r, n):
    """
    複利計算を行う関数
    
    Parameters:
        P (float): 元本（現在価値）
        r (float): 年利率
        n (int): 投資期間（年数）
    
    Returns:
        np.ndarray: 各年の金額の配列
    """
    years = np.arange(1, n+1)
    A = P * (1 + r)**years
    return A

compound_interest 関数は、与えられた元本$ (P) $、年利率$ (r) $、投資期間$ (n) $に基づいて複利計算を行います。
各年の金額の配列を返します。

パラメータの設定

1
2
3

P = 1000  # 元本
r = 0.05  # 年利率 (5%)
n = 10    # 投資期間（10年）

P は元本（投資の始めの金額）を表します。
r は年利率を表します。ここでは$ 5% $を表す$ 0.05 $が設定されています。
n は投資期間（年数）を表します。ここでは$ 10 $年が設定されています。

複利計算の実行

1	investment_values = compound_interest(P, r, n)

compound_interest 関数を使用して、指定されたパラメータで複利計算を実行し、各年の金額の配列を取得します。

グラフの描画

plt.plot(np.arange(1, n+1), investment_values, marker='o')
plt.title('Compound Interest over {} Years'.format(n))
plt.xlabel('Years')
plt.ylabel('Investment Value')
plt.grid(True)
plt.show()

plt.plot() は、与えられたデータをプロットしてグラフを作成します。
ここでは、各年の金額の配列を横軸に対してプロットしています。
plt.title() はグラフのタイトルを設定します。
plt.xlabel() と plt.ylabel() はそれぞれ横軸と縦軸のラベルを設定します。
plt.grid(True) はグリッド線を表示します。
plt.show() は、グラフを表示します。

これにより、元本$ (P) $を元にした複利計算の結果が$ 10 $年間の投資期間にわたってグラフ化されます。

結果解説

[実行結果]

このグラフは、投資の元本$ (P) $、年利率$ (r) $、投資期間$ (n) $に基づいて計算された複利効果を示しています。

横軸は時間を表し、投資期間が経過するにつれて増加します。
縦軸は投資の価値を表し、元本$ (P) $から始まり、時間が経つにつれて複利効果により増加していきます。

具体的には、投資期間の各年における投資の価値が点で示されています。
この点は、元本$ (P) $を年利率$ (r) $で複利計算した結果を示しています。
グラフ全体として、時間が経過するにつれて投資の価値が増加していく様子が視覚化されています。

グラフのタイトルには、投資期間が何年かが示されており、横軸には各年が、縦軸には投資の価値がラベル付けされています。
また、グリッド線が描かれており、各年ごとの価値を読み取りやすくしています。

このグラフは、投資が時間の経過とともにどのように成長するかを視覚的に理解するのに役立ちます。