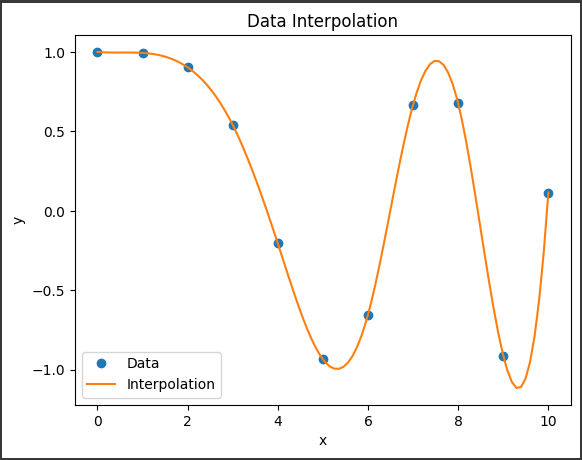
最小二乗法

scipyを使用して実際の問題である最小二乗法を解決し、結果をグラフ化します。

まず、scipyと必要なライブラリをインポートします。

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

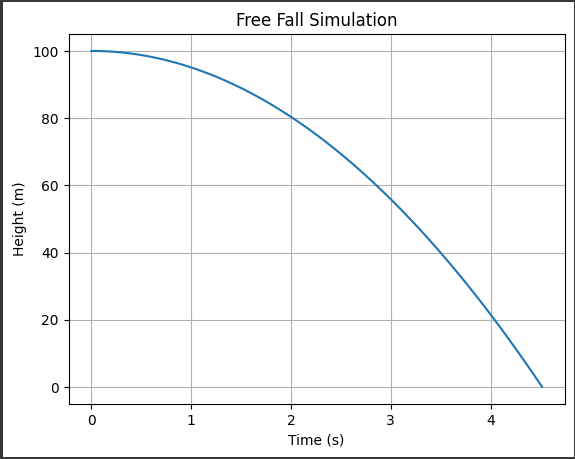
次に、データを作成します。ここでは、実際の問題として、ある物体の自由落下の時間と距離の関係を考えます。

1
2

time = np.array([0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0])
distance = np.array([0.05, 0.20, 0.45, 0.80, 1.25, 1.80, 2.45, 3.20, 4.05, 5.00])

次に、最小二乗法を使用してデータをフィットさせる関数を定義します。

1
2

def linear_func(x, a, b):
    return a * x + b

最小二乗法を実行し、最適なパラメータを取得します。

1
2

params, params_covariance = curve_fit(linear_func, time, distance)
a, b = params

結果をグラフ化します。

1
2
3
4
5
6
7

plt.scatter(time, distance, label='Data')
plt.plot(time, linear_func(time, a, b), label='Linear Fit')
plt.xlabel('Time')
plt.ylabel('Distance')
plt.title('Linear Fit using Least Squares Method')
plt.legend()
plt.show()

これにより、データポイントに最も適合する直線が表示されます。

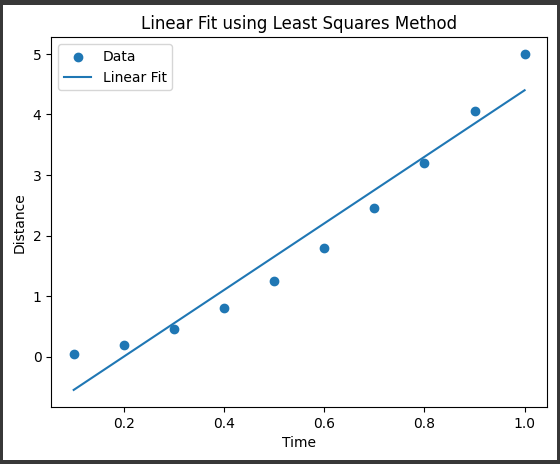
グラフ解説

このグラフは、時間と距離の関係を示しています。
x軸は時間を表し、y軸は距離を表しています。
データポイントは青い点で表示されており、それぞれの点は実際の観測値を表しています。

また、青い線は最小二乗法によってフィットされた回帰直線を表しています。
この回帰直線は、データポイントに最も適合する直線を表しており、時間と距離の関係を近似的に表現しています。

回帰直線の傾きと切片は、最小二乗法によって求められた最適なパラメータです。
傾きは直線の傾きを表し、切片はy軸との交点を表しています。
これらのパラメータは、時間と距離の関係を数値的に表現するために使用されます。

このグラフを通じて、時間と距離の関係を視覚的に理解することができます。
データポイントが回帰直線に近い位置にある場合、回帰直線がデータによく適合していることを示しています。
逆に、データポイントが回帰直線から離れている場合、回帰直線がデータに適合していないことを示しています。

このようなグラフを使用することで、時間と距離の関係を視覚化し、傾向やパターンを把握することができます。
また、回帰直線を使用することで、未知の時間における距離を予測することも可能です。

データ補間

Scipyを使用してデータの補間（補完）を行い、結果をグラフ化する例をご紹介します。

例として、以下のようなデータセットを考えます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

# サンプルデータの作成
x = np.linspace(0, 10, num=11, endpoint=True)
y = np.cos(-x**2/9.0)

# 補間関数の作成
f = interp1d(x, y, kind='cubic')

# 補間結果の計算
x_interp = np.linspace(0, 10, num=100, endpoint=True)
y_interp = f(x_interp)

# グラフのプロット
plt.plot(x, y, 'o', label='Data')
plt.plot(x_interp, y_interp, label='Interpolation')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Data Interpolation')
plt.legend()

# グラフの表示
plt.show()

このコードでは、numpy.linspace()関数を使用して等間隔のデータ点を作成し、それに対応するyの値を計算します。

次に、scipy.interpolate.interp1d()関数を使用してデータの補間関数を作成します。
ここでは、kind='cubic'を指定して3次のスプライン補間を行っています。

最後に、補間関数を使用して新しいxの値に対応するyの値を計算し、元のデータと補間結果をグラフ化して表示します。

この例では、Scipyを使用してデータの補間を行い、補間結果をグラフ化しています。
補間によって、元のデータに存在しないxの値に対応するyの値を推定することができます。

グラフ解説

上記のグラフは、データの補間結果を示しています。

青い点で示されているのは、元のデータセットです。
このデータセットは、0から10までの範囲で等間隔に取られた11個のデータポイントで構成されています。
各データポイントは、関数 $y = cos(-x^2/9.0)$ に基づいて計算されました。

補間関数を使用して、元のデータセットを補間することで、新しいxの値に対応するyの値を推定します。
補間関数は、3次のスプライン補間を使用しています。
補間結果は、補間されたデータポイントを結ぶ滑らかな曲線で表されます。

補間結果は、オレンジ色の線で示されています。
この曲線は、元のデータポイントをなめらかに結んでおり、元のデータセットの間の値を推定しています。
補間によって、元のデータセットに存在しないxの値に対応するyの値を推定することができます。

自由落下シミュレーション

Scipyを使用して物体の自由落下の運動をシミュレーションし、結果をグラフ化してみましょう。

以下のコードでは、物体の初期の高さと重力加速度を入力として受け取り、物体の自由落下の運動をシミュレーションします。

シミュレーション結果を時間と物体の高さの関係でグラフ化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt
from scipy.constants import g

def simulate_free_fall(initial_height):
    time = np.linspace(0, np.sqrt(2 * initial_height / g), 100)  # 0から物体が地面に到達するまでの時間を100等分
    height = initial_height - 0.5 * g * time**2  # 物体の高さを計算

    return time, height

# 初期高さと重力加速度を設定
initial_height = 100.0  # 初期高さ（任意の値）
gravity = g  # 重力加速度（地球の場合は9.8 m/s^2）

# 自由落下の運動をシミュレーション
time, height = simulate_free_fall(initial_height)

# 結果をグラフ化
plt.plot(time, height)
plt.xlabel('Time (s)')
plt.ylabel('Height (m)')
plt.title('Free Fall Simulation')
plt.grid(True)
plt.show()

このコードでは、numpyを使用して時間を0から物体が地面に到達するまでの時間に分割し、matplotlibを使用して結果をグラフ化しています。
x軸には時間（秒）、y軸には物体の高さ（メートル）を表示しています。

このグラフを通じて、物体が自由落下する際の高さの変化を視覚的に確認することができます。
時間が経つにつれて、物体の高さが減少していく様子がわかります。

グラフ解説

このグラフは、物体の自由落下の運動をシミュレーションした結果を表しています。

x軸は時間（秒）を表し、y軸は物体の高さ（メートル）を表しています。
グラフの形状は、物体が自由落下する過程で高さがどのように変化するかを示しています。

初期の高さが100メートルと仮定されている場合、物体は時間が経つにつれて高度が減少していきます。
最初は高さが減少する速度が緩やかですが、時間が経つにつれて減速し、最終的に地面に到達します。

グラフの形状は、放物線のような曲線となっています。
これは、物体が自由落下中に重力によって加速されるためです。
物体が自由落下する過程で、高さの変化は時間の二乗に比例して減少します。

このグラフを通じて、物体の自由落下の運動を視覚的に理解することができます。
時間が経つにつれて、物体の高さがどのように変化するかを確認できます。
また、初期高さや重力加速度を変更することで、グラフの形状がどのように変わるかを試すこともできます。

最適化問題

Scipyを使用して最適化問題を解決し、結果をグラフ化する例をご紹介します。

最適化問題の一つとして、以下のような関数の最小値を求める問題を考えてみましょう。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 最小化する関数
def objective(x):
    return (x[0] - 3) ** 2 + (x[1] - 4) ** 2

# 初期値
x0 = np.array([0, 0])

# 最適化の実行
result = minimize(objective, x0)

# 結果の表示
print("最小値:", result.fun)
print("最適解:", result.x)

# グラフの作成
x = np.linspace(-10, 10, 100)
y = np.linspace(-10, 10, 100)
X, Y = np.meshgrid(x, y)
Z = (X - 3) ** 2 + (Y - 4) ** 2

# グラフのプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, cmap='viridis')
ax.scatter(result.x[0], result.x[1], result.fun, color='r', label='Minimum')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('f(x, y)')
ax.set_title('Optimization')
ax.legend()

# グラフの表示
plt.show()

このコードでは、objectiveという関数を最小化する問題を考えます。

minimize関数を使用して最適化を実行し、最小値と最適解を表示します。

また、2次元の関数を3Dグラフとしてプロットするために、matplotlibのplot_surface関数を使用します。

最適解を赤い点で表示し、グラフにタイトルや軸ラベルを追加します。

この例では、最小化する関数が2次元のパラメータに依存しているため、最適解を容易に可視化することができます。

しかし、Scipyの最適化機能は高次元の問題にも適用することができます。

Scipyの最適化機能を使用することで、現実の問題において最適なパラメータや条件を見つけることができます。

これにより、例えば機械学習モデルのパラメータチューニングや最適な経路の計画など、さまざまな問題に対して最適な解を見つけることができます。

グラフ解説

先ほどの最適化問題の実行結果のグラフについて詳しく説明します。

このグラフは、2次元の関数を3Dプロットしたものです。
横軸と縦軸はそれぞれ変数xとyの値を表し、縦軸は関数の値f(x, y)を表しています。

グラフの曲面は、関数 (x - 3) ** 2 + (y - 4) ** 2 の値を示しています。
この関数は、点 (3, 4) を中心とする放物線のような形状を持ちます。
最小値を求めるために、Scipyの最適化機能が使用されました。

最適化の結果、最小値は result.fun として表示されます。
また、最適解は (result.x[0], result.x[1]) として表示されます。

グラフ上の赤い点は、最適解を示しています。
この点は、関数の最小値に対応する変数xとyの値を表しています。

このグラフを通じて、最適化問題の解がどのように見つかったかを視覚的に理解することができます。
最適解が関数の谷底に位置していることがわかります。

このようなグラフの可視化は、最適化問題の解析や結果の評価に役立ちます。
特に、高次元の問題では、グラフを通じて最適解の特性や関数の形状を理解することが重要です。

非線形方程式

Scipyを使用して、非線形方程式を解く問題を考えてみましょう。

具体的には、以下の非線形方程式を解くことを目指します。

$ x^2 + y^2 = 25 $
$ x^2 - y = 7 $

この方程式を解くために、Scipyのfsolve()関数を使用します。

以下のコードをご参考ください。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve

def equations(vars):
    x, y = vars
    eq1 = x**2 + y**2 - 25
    eq2 = x**2 - y - 7
    return [eq1, eq2]

# 初期値を設定します
initial_guess = [0, 0]

# 方程式を解きます
solution = fsolve(equations, initial_guess)
print("Solution: x =", solution[0], ", y =", solution[1])

x_solution, y_solution = solution[0], solution[1]

# グラフの範囲を設定します
x = np.linspace(-10, 10, 400)
y = np.linspace(-10, 10, 400)

# グリッドを作成します
X, Y = np.meshgrid(x, y)

# 方程式を計算します
Z1 = X**2 + Y**2 - 25
Z2 = X**2 - Y - 7

# グラフを作成します
fig, ax = plt.subplots()
ax.contour(X, Y, Z1, levels=[0], colors='r', label='x^2 + y^2 = 25')
ax.contour(X, Y, Z2, levels=[0], colors='b', label='x^2 - y = 7')
ax.plot(x_solution, y_solution, 'go', label='Solution')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.legend()
plt.grid(True)
plt.show()

このコードでは、fsolve()関数を使用して非線形方程式の解を求め、解をx_solutionとy_solutionに格納します。

次に、グラフの範囲を設定し、np.meshgrid()関数を使用してグリッドを作成します。

方程式を計算し、contour()関数を使用して等高線プロットを作成します。

また、解をplot()関数を使用してプロットし、グラフに表示します。

上記のコードを実行すると、非線形方程式の解を含むグラフが表示されます。

赤い等高線は方程式 $x^2 + y^2 = 25$ を表し、青い等高線は方程式 $x^2 - y = 7$ を表します。

緑の点は、求めた解を示しています。

このように、ScipyとMatplotlibを組み合わせることで、非線形方程式の解を視覚化することができます。

グラフを通じて、方程式の解がどのように見えるかを直感的に理解することができます。

SciPyを使用して、ある物質の温度変化に関する問題を考え、その結果をグラフ化します。

物質の冷却

ある物質の冷却過程を考えます。
物質の初期温度が $100℃$ であり、周囲の温度が $25℃$ です。

物質の冷却は、ニュートンの冷却法則に従います。
物質の温度T（℃）は以下の式で与えられます。

$ \frac{dT}{dt} = -k \cdot (T - T_{\text{ambient}}) $

ここで、$ (k) $ は冷却係数であり、$(T_{\text{ambient}}) $は周囲の温度です。
物質の冷却係数は$0.07$とします。

この冷却過程をSciPyを使用して解き、物質の温度変化を0から100秒までシミュレートし、結果をグラフで表示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# 冷却係数
k = 0.07
# 初期温度
T_initial = 100
# 周囲の温度
T_ambient = 25

# モデル式
def model(T, t):
    dTdt = -k * (T - T_ambient)
    return dTdt

# 時間範囲
t = np.linspace(0, 100, 100)

# 初期条件
T0 = [T_initial]

# 微分方程式を解く
T = odeint(model, T0, t)

# 結果をグラフで表示
plt.plot(t, T)
plt.xlabel('Time (s)')
plt.ylabel('Temperature (C)')
plt.title('Cooling of a Substance')
plt.grid(True)
plt.show()

このコードは、物質の冷却過程をシミュレートし、時間に対する温度の変化をグラフ化します。

初めは100℃で始まり、徐々に周囲の温度に近づいていく様子が分かります。

ソースコード解説

このソースコードは、Pythonプログラムで物質の冷却過程をモデル化し、結果をグラフとして表示するものです。
以下にソースコードの詳細な説明を行います。

1. ライブラリのインポート:

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

• numpy: 数値計算をサポートするライブラリ。
• matplotlib.pyplot: データをグラフで描画するためのライブラリ。
• scipy.integrate.odeint: 常微分方程式を数値的に解くための関数。

2. パラメータの設定:

1
2
3

k = 0.07  # 冷却係数
T_initial = 100  # 初期温度
T_ambient = 25   # 周囲の温度

• k: 物質の冷却速度を示す冷却係数。
• T_initial: 物質の初期温度。
• T_ambient: 周囲の温度。

3. モデル式の定義:

1
2
3

def model(T, t):
    dTdt = -k * (T - T_ambient)
    return dTdt

• model(T, t): 冷却過程のモデル式を表す関数。
  ニュートンの冷却法則に基づき、温度変化率 dTdt を計算して返します。

4. 時間範囲の設定:

1

t = np.linspace(0, 100, 100)

• np.linspace(0, 100, 100): 0から100までの範囲を100個の等間隔な点で区切った配列を生成。
  時間の経過を表す配列 t。

5. 初期条件の設定:

1

T0 = [T_initial]

• T0: 初期温度を要素とするリスト。
  微分方程式の初期条件として使用されます。

6. 微分方程式の解法:

1

T = odeint(model, T0, t)

• odeint(model, T0, t): 微分方程式 model を初期条件 T0 から解いて、時間経過に伴う温度の変化を計算します。

7. 結果のグラフ表示:

1
2
3
4
5
6

plt.plot(t, T)
plt.xlabel('Time (s)')
plt.ylabel('Temperature (C)')
plt.title('Cooling of a Substance')
plt.grid(True)
plt.show()

• plt.plot(t, T): 時間に対する温度の変化を折れ線グラフとして描画。
• plt.xlabel('Time (s)'): X軸のラベルを設定。
• plt.ylabel('Temperature (C)'): Y軸のラベルを設定。
• plt.title('Cooling of a Substance'): グラフのタイトルを設定。
• plt.grid(True): グリッドを表示。
• plt.show(): グラフを表示。

このソースコードは、微分方程式を解いて物質の冷却過程をシミュレートし、結果をグラフで可視化する基本的な例です。

グラフ解説

生成されるグラフは、物質の冷却過程を時間の経過に伴って示しています。

以下にその詳細な説明を行います。

グラフの横軸（X軸）は時間（秒）を示しており、縦軸（Y軸）は物質の温度（摂氏）を示しています。

初期条件として、物質の初期温度は$100℃$です。
物質は周囲の温度である$25℃$に徐々に近づく過程が描かれています。
冷却係数 $(k)$ が$0.07$と設定されており、物質の温度変化はニュートンの冷却法則に従っています。

グラフの形状は、指数的な減少を示しています。
最初の数秒間は温度の変化が大きく、急速に冷却が進行しています。
しかし、時間が経つにつれて温度の変化は緩やかになり、周囲の温度に収束していきます。
つまり、物質は周囲の環境に達するまで冷却されていくことが分かります。

グラフの右上に近づくにつれ、温度の変化はゆっくりとなり、最終的には周囲の温度に収束していることが確認できます。
これは、冷却過程が進むにつれて温度の差が小さくなるためです。

このグラフは、物質の冷却過程が時間とともにどのように進行するかを示しており、物理的な現象の理解やモデリングに役立つ情報を提供しています。

給与データ分析

scipyを使用して現実的な統計問題を解決し、その結果をグラフ化する例を示します。

この例では、ある架空の企業の従業員の給与データを扱います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt

# 架空の給与データ（千円）
salaries = np.array([30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100])

# 平均と標準偏差の計算
mean_salary = np.mean(salaries)
std_deviation = np.std(salaries)

# 正規分布に基づく確率密度関数（PDF）の計算
x = np.linspace(mean_salary - 3 * std_deviation, mean_salary + 3 * std_deviation, 100)
pdf = stats.norm.pdf(x, mean_salary, std_deviation)

# ヒストグラムと正規分布の確率密度関数をグラフ化
plt.figure(figsize=(10, 6))
plt.hist(salaries, bins=10, density=True, alpha=0.6, color='blue', label='Empirical Data')
plt.plot(x, pdf, color='red', label='Normal Distribution PDF')
plt.xlabel('Salary (Thousands of Yen)')
plt.ylabel('Probability Density')
plt.title('Salary Distribution and Normal Distribution')
plt.legend()
plt.grid(True)
plt.show()

このコードは、架空の給与データを用いて、ヒストグラムと正規分布の確率密度関数を同じグラフ上に表示します。
データの分布と正規分布の形状を比較することができます。

ご自身のデータを使用して同様のアプローチを取ることで、実際の統計問題を解決し、結果を分かりやすくグラフ化することができます。

データや問題の内容によって適切な統計手法やグラフの種類が異なる場合がありますので、その点を考慮してください。

グラフ解説

上記グラフは、架空の企業の従業員の給与データとそれに対する正規分布の確率密度関数（PDF）を比較しています。

以下に、このグラフから得られる情報について詳しく説明します。

1. データの分布:

青色のヒストグラムは、架空の企業の従業員の給与データを表しています。
横軸は給与額（千円）、縦軸は確率密度を示しています。
ヒストグラムの各バーは、特定の給与範囲内の従業員数を示しており、データがどのように分布しているかを可視化しています。

2. 正規分布の確率密度関数:

赤色の線は、計算された正規分布の確率密度関数（PDF）を表しています。
この曲線は、データが正規分布に従っている場合の予測される分布を示しています。
正規分布は平均と標準偏差によって特徴付けられる確率分布で、多くの自然現象や統計データがこの分布に近い形状を取ることがあります。

3. 平均と標準偏差:

ヒストグラムのデータの中心付近にあるバーの位置は、データの平均給与額を示しています。
また、データのバーの広がり具合は、データのばらつきや分散を示しています。
正規分布の確率密度関数のピークは、平均給与額に位置しています。

4. データと正規分布の比較:

このグラフを通じて、データと正規分布の形状や特性を比較することができます。
データが正規分布に近い形状をしている場合、ヒストグラムのバーが赤い正規分布曲線に近づくことが期待されます。

5. 外れ値や歪み:

もしデータが正規分布から大きく外れていたり、非対称な形状をしている場合、ヒストグラムと正規分布の差異が観察されるかもしれません。
この差異は、データ内の外れ値や特異なパターンを示す兆候となる可能性があります。

要するに、このグラフは給与データの分布を視覚化し、そのデータが正規分布に従っているかどうかを確認するのに役立ちます。
データの特性や分布について洞察を得ることができるでしょう。

糖尿病 進行予測

scikit-learnを使用して、糖尿病患者のデータを元に、糖尿病の進行を予測する簡単な統計問題を解いてみましょう。

データセットには、糖尿病患者の年齢や血圧などの特徴量と、1年後の疾患進行の定量的な指標が含まれています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix

# データの準備（糖尿病データセットを使用）
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
X = diabetes.data
y = (diabetes.target > 100).astype(int)  # 1年後の進行が進行するかどうか

# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ロジスティック回帰モデルの作成と学習
model = LogisticRegression()
model.fit(X_train, y_train)

# テストデータで予測
y_pred = model.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)

# 結果の出力
print("Accuracy:", accuracy)
print("Confusion Matrix:\n", conf_matrix)

# 結果をグラフ化
plt.figure(figsize=(8, 6))
plt.imshow(conf_matrix, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion Matrix')
plt.colorbar()
plt.xticks([0, 1], ['No Progression', 'Progression'])
plt.yticks([0, 1], ['No Progression', 'Progression'])
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()

このコードは、ロジスティック回帰を用いて糖尿病の進行を予測し、結果を混同行列（Confusion Matrix）としてグラフ化しています。

[実行結果]

混同行列は、実際のクラスとモデルの予測結果を交差させた表で、予測の正確さを評価するのに役立ちます。

グラフ化によって、予測がどれだけ正確か、またどのクラスがより誤って予測されているかを視覚的に確認することができます。

ソースコード解説

コードの各部分を詳しく説明します。

1. ライブラリのインポート:

1
2
3
4
5

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix

必要なライブラリやモジュールをインポートしています。
numpyは数値計算のため、matplotlib.pyplotはグラフの描画のため、train_test_splitはデータの分割のため、LogisticRegressionはロジスティック回帰モデルのため、accuracy_scoreとconfusion_matrixはモデル評価のために使用されます。

2. データの準備:

1
2
3

diabetes = load_diabetes()
X = diabetes.data
y = (diabetes.target > 100).astype(int)

load_diabetes()を使って糖尿病のデータセットを読み込み、特徴量(X)と目的変数(y)を取得しています。
目的変数は1年後の進行が進行するかどうかを示すバイナリ値（0または1）に変換しています。

3. データの分割:

1

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

train_test_splitを使用して、データをトレーニングセットとテストセットに分割しています。
test_sizeはテストセットの割合を示し、random_stateはランダムな分割を制御するシード値です。

4. モデルの構築と学習:

1
2

model = LogisticRegression()
model.fit(X_train, y_train)

LogisticRegressionクラスのインスタンスを作成し、トレーニングデータを用いてモデルを学習させています。

5. テストデータで予測:

1

y_pred = model.predict(X_test)

学習済みモデルを使ってテストデータの予測を行います。

6. モデルの評価:

1
2

accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)

accuracy_scoreで予測の正確さを評価し、confusion_matrixで混同行列を計算しています。

7. 結果の出力:

1
2

print("Accuracy:", accuracy)
print("Confusion Matrix:\n", conf_matrix)

正確さと混同行列の結果を出力します。

8. 結果のグラフ化:

1
2
3
4
5
6
7
8
9

plt.figure(figsize=(8, 6))
plt.imshow(conf_matrix, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion Matrix')
plt.colorbar()
plt.xticks([0, 1], ['No Progression', 'Progression'])
plt.yticks([0, 1], ['No Progression', 'Progression'])
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()

混同行列をカラーマップを使って可視化しています。

X軸が予測値、Y軸が実際の値を表し、それぞれのクラスを示すラベルが付いています。

カラーバーが数値と色の関連を示しています。

結果解説

先ほどのコードによって生成される混同行列のグラフは、モデルの予測結果と実際のクラスを対比させて、モデルの性能を可視化するためのものです。

以下で各要素の詳細を説明します。

グラフの要素:

• カラーマップ (Color Map):
  グラフの色は、混同行列の値を示します。
  色の濃淡は値の大小を表し、色が明るいほど大きな値を持つことを示します。
  この例では、青系のカラーマップ（cmap=plt.cm.Blues）が使用されています。

• 軸 (Axes):
  グラフの軸は、実際のクラスとモデルの予測クラスを示しています。
  X軸が「Predicted（予測値）」で、Y軸が「Actual（実際の値）」です。
  各軸には「No Progression（進行なし）」と「Progression（進行あり）」の2つのクラスがあります。

• 軸ラベル (Axis Labels):
  軸ラベルは各軸のクラスを示しており、X軸とY軸にそれぞれのクラスのラベルが表示されます。

• タイトル (Title):
  グラフの上部には「Confusion Matrix」というタイトルがあります。
  これは混同行列を表すグラフであることを示しています。

• カラーバー (Colorbar):
  カラーバーは、色と値の関係を示すための尺度です。カラーバーによって、色の濃淡と実際の値の関連が可視化されます。

混同行列の各要素:

• 真陽性 (True Positive, TP):
  実際のクラスが「Progression」であり、モデルが「Progression」と正しく予測した数です。

• 真陰性 (True Negative, TN):
  実際のクラスが「No Progression」であり、モデルが「No Progression」と正しく予測した数です。

• 偽陽性 (False Positive, FP):
  実際のクラスが「No Progression」であり、モデルが誤って「Progression」と予測した数です。
  誤検知を示します。

• 偽陰性 (False Negative, FN):
  実際のクラスが「Progression」であり、モデルが誤って「No Progression」と予測した数です。
  逃してしまったケースを示します。

これらの要素をグラフから読み取ることで、モデルの予測性能がどれだけ良いか、特に誤分類の傾向を確認することができます。

例えば、偽陽性や偽陰性が多い場合、モデルが特定のクラスをうまく識別できていない可能性があります。

制約条件を持つ最適化問題

制約条件を持つ最適化問題を解くためには、scipy.optimizeモジュールを使用することが一般的です。

以下は、scipyを使用して制約条件のある最適化問題を解くサンプルコードです。

この例では、制約条件付きの2次元目的関数を最小化する問題を考えます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 目的関数の定義
def objective(x):
    return x[0]**2 + x[1]**2

# 制約条件
def constraint(x):
    return x[0] + x[1] - 1

# 初期値
x0 = np.array([0.5, 0.5])

# 制約条件付き最適化
constraints = {'type': 'eq', 'fun': constraint}
result = minimize(objective, x0, constraints=constraints)

# 結果の表示
print("最適な解:", result.x)
print("最小値:", result.fun)

[実行結果]

グラフ化

次に、結果をグラフ化してみましょう。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 目的関数を等高線プロット
x = np.linspace(-2, 2, 400)
y = np.linspace(-2, 2, 400)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2

plt.contour(X, Y, Z, levels=np.logspace(-1, 2, 10), cmap='viridis')

# 制約条件をプロット
plt.plot(x, 1 - x, '-r', label='x + y = 1')

# 最適解をプロット
plt.plot(result.x[0], result.x[1], 'ro', label='最適解')

plt.xlabel('x')
plt.ylabel('y')
plt.title('Constrained Optimization')
plt.legend()
plt.show()

このコードでは、2次元の目的関数を最小化しながら、制約条件 x + y = 1 を満たす最適解を求めています。

結果は等高線プロットとして表示され、最適解は赤い点で示されます。

なお、制約条件のある最適化問題は様々な種類があり、それぞれ異なるアプローチが必要です。

上記の例は一般的なサンプルであり、実際の問題に応じて適切なアルゴリズムや制約条件の設計が必要です。

[実行結果]

異常検出

異常検出の例として、シンプルなユースケースとして1次元のデータで異常を検出することを考えてみましょう。

以下は、正規分布に従うデータに対して異常を検出する例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import IsolationForest

# データ生成
np.random.seed(42)
normal_data = np.random.normal(loc=0, scale=1, size=1000)
anomalies = np.array([4, 5, -3])  # 異常値の追加

# データと異常値を結合
data = np.concatenate([normal_data, anomalies])

# データのプロット
plt.figure(figsize=(10, 6))
plt.scatter(range(len(data)), data, marker='x', color='blue', label='Normal')
plt.scatter(range(len(normal_data), len(data)), anomalies, marker='o', color='red', label='Anomaly')
plt.xlabel('Sample Index')
plt.ylabel('Value')
plt.title('Anomaly Detection Example')
plt.legend()
plt.show()

# Isolation Forestモデルの構築と異常検出
model = IsolationForest(contamination=0.05, random_state=42)  # contaminationは異常値の割合
model.fit(data.reshape(-1, 1))

# データの異常スコアを予測
anomaly_scores = model.decision_function(data.reshape(-1, 1))

# 異常スコアのプロット
plt.figure(figsize=(10, 6))
plt.plot(anomaly_scores, marker='o', linestyle='-', color='green')
plt.xlabel('Sample Index')
plt.ylabel('Anomaly Score')
plt.title('Anomaly Scores')
plt.show()

このコードでは、正規分布に従うデータに3つの異常値を追加しています。

Isolation Forestアルゴリズムを使用して異常検出を行い、異常スコアをプロットしています。

異常スコアが閾値を超えるデータポイントは、異常として検出されたとみなすことができます。

なお、実際のデータではより多くの特徴量や高次元データを扱うことになるため、適切なデータの前処理やモデルの調整が必要です。

また、異常の定義や異常値の割合に応じてcontaminationパラメータを調整する必要があります。

ソースコード解説

以下にコードの各部分の詳細な説明を行います。

1. モジュールのインポート:

最初の数行では、必要なライブラリとモジュールをインポートしています。

• numpy（npとしてエイリアス）: 数値計算用のライブラリ。
• matplotlib.pyplot（pltとしてエイリアス）: データの可視化用のライブラリ。
• IsolationForestクラス: Scikit-learnの異常検出アルゴリズムであるIsolation Forestを提供するクラス。

2. データの生成と準備:

• normal_data: 正規分布に従うランダムなデータを生成しています。
  平均 (loc) は0、標準偏差 (scale) は1で、サイズは1000です。
• anomalies: 異常値の配列を手動で定義しています。

3. データと異常値のプロット:

• plt.scatter: データと異常値をプロットしています。
  青い「x」マーカーは正常なデータポイントを示し、赤い「o」マーカーは異常値を示します。
  X軸はサンプルのインデックス、Y軸は値です。

4. Isolation Forestモデルの構築と異常検出:

• IsolationForestのインスタンスを作成しています。
  contaminationパラメータは異常値の割合を指定します。
  random_stateは乱数のシードを固定します。
• model.fit: モデルをデータに適合させます。

5. データの異常スコアを予測:

• model.decision_function: データポイントの異常スコアを計算します。
  異常スコアは、モデルがデータポイントを異常とみなす確信度の尺度です。

6. 異常スコアのプロット:

• plt.plot: データポイントの異常スコアをプロットしています。
  異常スコアが低いほど正常、高いほど異常と判断される可能性が高くなります。
  X軸はサンプルのインデックス、Y軸は異常スコアです。

このコードは、Isolation Forestアルゴリズムを使用して異常検出を行い、異常スコアをプロットして視覚化するサンプルです。

ただし、実際のケースではデータの前処理、ハイパーパラメータの調整、適切なモデルの選択などが必要です。

結果解説

異常検出の結果として表示される2つのグラフについて、詳しく説明します。

1. データと異常値のプロット:

このグラフは、元のデータと追加した異常値を含むデータポイントを表示しています。
以下の要素に注意してください：

• 青い「x」マーカー:
  正常なデータポイントを表しています。これらは正規分布に従うランダムなデータです。
• 赤い「o」マーカー:
  異常値を表しています。これらはわざとデータに追加された異常な値です。

このプロットは、異常検出のタスクを視覚的に理解するのに役立ちます。
異常値が通常のデータポイントからどれだけ外れているかが分かります。

2. 異常スコアのプロット:

このグラフは、Isolation Forestアルゴリズムによって計算された異常スコアを示しています。
以下の要素に注意してください：

• 縦軸 (Y軸): 異常スコアを表しています。
  スコアが低いほどデータポイントは正常、高いほど異常と判断された可能性が高いです。
• 横軸 (X軸): データポイントのインデックスを表しています。

グリーンの線で表されたプロットは、各データポイントの異常スコアを示しています。
異常スコアが閾値を超えるデータポイントは、異常として検出されたとみなされます。

これらのグラフは、異常検出のプロセスを理解し、異常検出アルゴリズムのパフォーマンスを評価する際に役立ちます。

異常スコアを基にして異常を検出するため、グラフから異常値がどれだけ明確に特定されているかを確認することが重要です。