糖尿病 進行予測 scikit-learn

糖尿病 進行予測

scikit-learnを使用して、糖尿病患者のデータを元に、糖尿病の進行を予測する簡単な統計問題を解いてみましょう。

データセットには、糖尿病患者の年齢や血圧などの特徴量と、1年後の疾患進行の定量的な指標が含まれています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix

# データの準備（糖尿病データセットを使用）
from sklearn.datasets import load_diabetes
diabetes = load_diabetes()
X = diabetes.data
y = (diabetes.target > 100).astype(int)  # 1年後の進行が進行するかどうか

# データをトレーニングセットとテストセットに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# ロジスティック回帰モデルの作成と学習
model = LogisticRegression()
model.fit(X_train, y_train)

# テストデータで予測
y_pred = model.predict(X_test)

# モデルの評価
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)

# 結果の出力
print("Accuracy:", accuracy)
print("Confusion Matrix:\n", conf_matrix)

# 結果をグラフ化
plt.figure(figsize=(8, 6))
plt.imshow(conf_matrix, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion Matrix')
plt.colorbar()
plt.xticks([0, 1], ['No Progression', 'Progression'])
plt.yticks([0, 1], ['No Progression', 'Progression'])
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()

このコードは、ロジスティック回帰を用いて糖尿病の進行を予測し、結果を混同行列（Confusion Matrix）としてグラフ化しています。

[実行結果]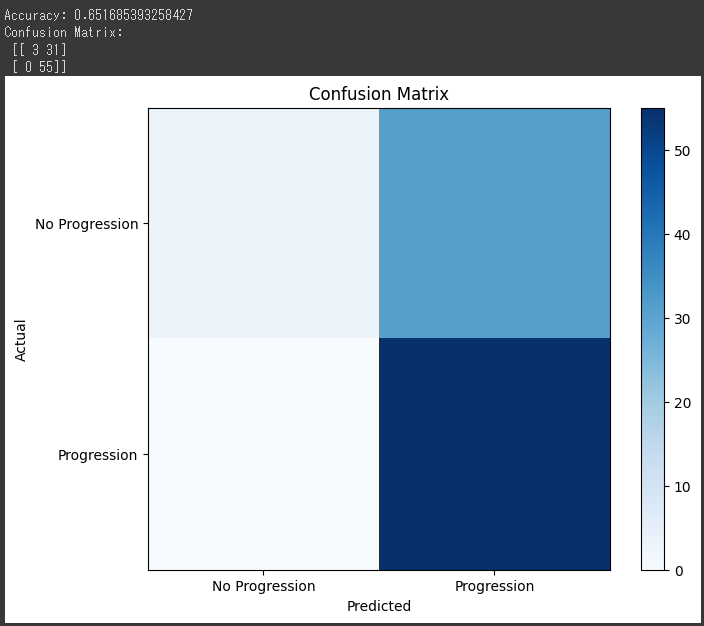

混同行列は、実際のクラスとモデルの予測結果を交差させた表で、予測の正確さを評価するのに役立ちます。

グラフ化によって、予測がどれだけ正確か、またどのクラスがより誤って予測されているかを視覚的に確認することができます。

ソースコード解説

コードの各部分を詳しく説明します。

1. ライブラリのインポート:

1
2
3
4
5
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix

必要なライブラリやモジュールをインポートしています。
numpyは数値計算のため、matplotlib.pyplotはグラフの描画のため、train_test_splitはデータの分割のため、LogisticRegressionはロジスティック回帰モデルのため、accuracy_scoreとconfusion_matrixはモデル評価のために使用されます。

2. データの準備:

1
2
3
diabetes = load_diabetes()
X = diabetes.data
y = (diabetes.target > 100).astype(int)

load_diabetes()を使って糖尿病のデータセットを読み込み、特徴量(X)と目的変数(y)を取得しています。
目的変数は1年後の進行が進行するかどうかを示すバイナリ値（0または1）に変換しています。

3. データの分割:

1
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

train_test_splitを使用して、データをトレーニングセットとテストセットに分割しています。
test_sizeはテストセットの割合を示し、random_stateはランダムな分割を制御するシード値です。

4. モデルの構築と学習:

1
2
model = LogisticRegression()
model.fit(X_train, y_train)

LogisticRegressionクラスのインスタンスを作成し、トレーニングデータを用いてモデルを学習させています。

5. テストデータで予測:

1
y_pred = model.predict(X_test)

学習済みモデルを使ってテストデータの予測を行います。

6. モデルの評価:

1
2
accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)

accuracy_scoreで予測の正確さを評価し、confusion_matrixで混同行列を計算しています。

7. 結果の出力:

1
2
print("Accuracy:", accuracy)
print("Confusion Matrix:\n", conf_matrix)

正確さと混同行列の結果を出力します。

8. 結果のグラフ化:

1
2
3
4
5
6
7
8
9
plt.figure(figsize=(8, 6))
plt.imshow(conf_matrix, interpolation='nearest', cmap=plt.cm.Blues)
plt.title('Confusion Matrix')
plt.colorbar()
plt.xticks([0, 1], ['No Progression', 'Progression'])
plt.yticks([0, 1], ['No Progression', 'Progression'])
plt.xlabel('Predicted')
plt.ylabel('Actual')
plt.show()

混同行列をカラーマップを使って可視化しています。

X軸が予測値、Y軸が実際の値を表し、それぞれのクラスを示すラベルが付いています。

カラーバーが数値と色の関連を示しています。

結果解説

先ほどのコードによって生成される混同行列のグラフは、モデルの予測結果と実際のクラスを対比させて、モデルの性能を可視化するためのものです。

以下で各要素の詳細を説明します。

グラフの要素:

  • カラーマップ (Color Map):
    グラフの色は、混同行列の値を示します。
    色の濃淡は値の大小を表し、色が明るいほど大きな値を持つことを示します。
    この例では、青系のカラーマップ（cmap=plt.cm.Blues）が使用されています。

  • 軸 (Axes):
    グラフの軸は、実際のクラスとモデルの予測クラスを示しています。
    X軸が「Predicted（予測値）」で、Y軸が「Actual（実際の値）」です。
    各軸には「No Progression（進行なし）」と「Progression（進行あり）」の2つのクラスがあります。

  • 軸ラベル (Axis Labels):
    軸ラベルは各軸のクラスを示しており、X軸とY軸にそれぞれのクラスのラベルが表示されます。

  • タイトル (Title):
    グラフの上部には「Confusion Matrix」というタイトルがあります。
    これは混同行列を表すグラフであることを示しています。

  • カラーバー (Colorbar):
    カラーバーは、色と値の関係を示すための尺度です。カラーバーによって、色の濃淡と実際の値の関連が可視化されます。

混同行列の各要素:

  • 真陽性 (True Positive, TP):
    実際のクラスが「Progression」であり、モデルが「Progression」と正しく予測した数です。

  • 真陰性 (True Negative, TN):
    実際のクラスが「No Progression」であり、モデルが「No Progression」と正しく予測した数です。

  • 偽陽性 (False Positive, FP):
    実際のクラスが「No Progression」であり、モデルが誤って「Progression」と予測した数です。
    誤検知を示します。

  • 偽陰性 (False Negative, FN):
    実際のクラスが「Progression」であり、モデルが誤って「No Progression」と予測した数です。
    逃してしまったケースを示します。

これらの要素をグラフから読み取ることで、モデルの予測性能がどれだけ良いか、特に誤分類の傾向を確認することができます。

例えば、偽陽性や偽陰性が多い場合、モデルが特定のクラスをうまく識別できていない可能性があります。