ベッセル関数
ベッセル関数は物理や数学で幅広く利用される特殊関数の一つです。
ベッセル関数の数式として、第一種ベッセル関数 $ ( J_n(x) ) $の例を示します:
$$
J_n(x) = \frac{1}{\pi} \int_{0}^{\pi} \cos(n\theta - x \sin \theta) , d\theta
$$
このベッセル関数をPythonでグラフ化するために、SciPyライブラリのベッセル関数を利用します。
以下がコードになります:
1 | import numpy as np |
このコードでは、scipy.special.jn を使用してベッセル関数を計算し、それをMatplotlibを使ってグラフ化しています。
[実行結果]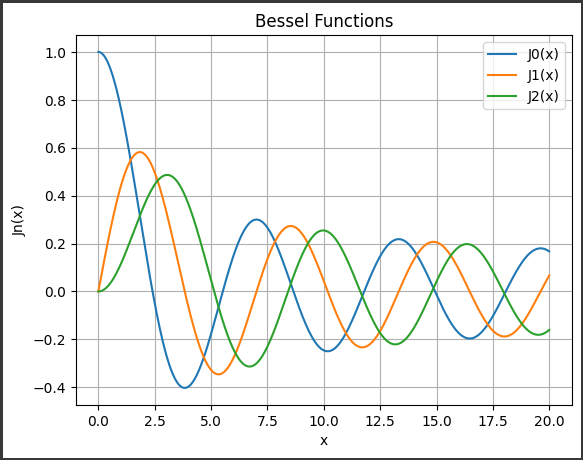
ソースコード解説
このコードは、Pythonでベッセル関数(Bessel Functions)を計算し、Matplotlibを使用してグラフ化するものです。
1. NumPyとMatplotlibのインポート:
numpyをnpとしてインポートし、行列計算や数値演算を行うための機能を利用します。matplotlib.pyplotをpltとしてインポートし、グラフ描画のための機能を利用します。
2. SciPyからベッセル関数のインポート:
scipy.specialモジュールからjn関数をインポートしています。
これはベッセル関数を計算するための関数です。
3. データの準備:
np.linspace(0, 20, 1000)によって、$0$から$20$の範囲を等間隔に$1000$点取得し、xに格納します。
4. ベッセル関数の計算とプロット:
forループでrange(3)を使用し、nが0から2まで変化します。jn(n, x)を使って、xに対する第一種ベッセル関数(n=0, 1, 2)を計算します。plt.plot(x, y, label=f'J{n}(x)')により、各nのベッセル関数をプロットします。labelを使って凡例を設定しています。
5. グラフの装飾:
plt.title、plt.xlabel、plt.ylabelを使って、タイトルや軸ラベルを設定します。plt.legend()で凡例を表示します。plt.grid(True)でグリッドを表示します。
6. グラフの表示:
plt.show()により、グラフを表示します。
このコードは、ベッセル関数を計算し、それをグラフ化しています。
それぞれのベッセル関数の振る舞いを可視化し、それが x の値に対してどのように変化するかを示しています。
グラフ解説
[実行結果]
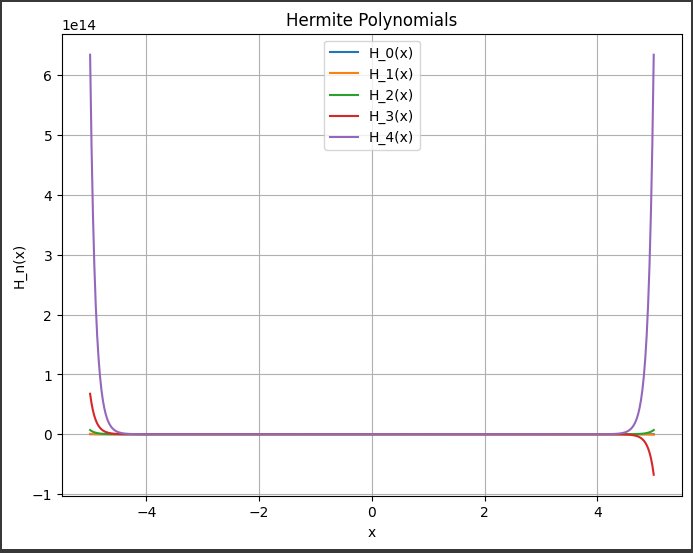
このグラフは、第一種ベッセル関数(Bessel Function of the First Kind)の値を示しています。
第一種ベッセル関数は微分方程式理論や物理学、工学など幅広い分野で重要な役割を果たす特殊関数です。
解析的な式で表されるこの関数は、x(横軸)と Jn(x)(縦軸)の関係を示しており、このグラフでは n=0、n=1、n=2 の3つのベッセル関数が描かれています。
n=0のベッセル関数(青の線)は、xが$0$のときに$1$に近づき、その後減少していきますxが大きくなるにつれて振動が小さくなり、$0$に収束します。n=1のベッセル関数(オレンジの線)は、xが$0$のときに$0$になり、xが増加するにつれて振動して$±1$の間を移動します。n=2のベッセル関数(緑の線)は、xが0のときに$0$になり、xが増加するにつれて振動が増幅し、2回の極小値と1回の極大値を持ちます。
xが大きくなるほど、ベッセル関数の振る舞いが規則的になり、特定のパターンに収束していく様子が観察されます。
このグラフは、数学的な特殊関数の性質を視覚的に理解するのに役立ちます。