シュレーディンガー方程式 SciPy

シュレーディンガー方程式

シュレーディンガー方程式は、量子力学における基本的な方程式の一つであり、波動関数を使って系の時間発展を記述します。

１次元の自由粒子のシュレーディンガー方程式は以下のように表されます。

$$
[ -\frac{\hbar^2}{2m} \frac + V(x)\psi = E\psi ]
$$

ここで、$ (\hbar) $はプランク定数の割合、$ (m) $は粒子の質量、$ (\psi) $は波動関数、$ (V(x)) $はポテンシャル関数、$ (E) $はエネルギーです。

この方程式を解析的に解くことは多くの場合難しいですが、数値的に解くことは可能です。

Pythonで数値解を求め、グラフ化するコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import eigh_tridiagonal

# パラメータ設定
h_bar = 1.0
m = 1.0
omega = 1.0  # 角振動数の設定
N = 1000
L = 10.0
x = np.linspace(0, L, N)
dx = x[1] - x[0]

# ポテンシャル関数を定義
def potential_function(x):
    return 0.5 * m * (omega**2) * x**2  # 調和振動子ポテンシャル

# 対角成分と非対角成分を計算
diagonal = np.ones(N) / dx**2 + potential_function(x)
off_diagonal = -0.5 * np.ones(N - 1) / dx**2

# トリディアゴナル行列を作成して固有値を求める
eigenvalues, eigenvectors = eigh_tridiagonal(diagonal, off_diagonal)

# 波動関数のグラフ化
plt.figure(figsize=(8, 6))
for i in range(4):  # 最初の４つの基底状態の波動関数を描画
    psi = eigenvectors[:, i]
    plt.plot(x, psi, label=f'n = {i+1}')

plt.title('Wavefunctions of the Quantum Harmonic Oscillator')
plt.xlabel('x')
plt.ylabel('psi(x)')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、単純な調和振動子ポテンシャルを持つシュレーディンガー方程式の基底状態の波動関数を計算し、プロットしています。

これにより、最初の４つの基底状態の波動関数が描画されます。

[実行結果]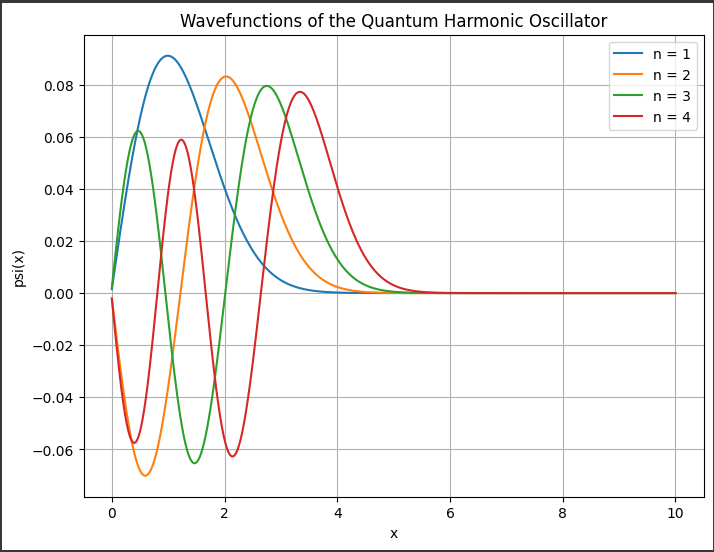

ソースコード解説

このコードは、量子調和振動子のポテンシャルに対するシュレーディンガー方程式の固有値問題を解き、最初の４つの基底状態の波動関数をプロットしています。

1. パラメータ設定:

  • $ ( \hbar ) $: プランク定数
  • $ ( m ) $: 粒子の質量
  • $ ( \omega ) $: 角振動数
  • $ ( N ) $: 空間分割の数
  • $ ( L ) $: 空間の長さ
  • $ ( x ) $: 空間の区間

2. ポテンシャル関数:

potential_function(x)で定義され、量子調和振動子ポテンシャル$ ( \frac{1}{2} m \omega^2 x^2 ) $を表します。

3. 対角成分と非対角成分の計算:

トリディアゴナル行列の対角成分と非対角成分を計算します。

4. eigh_tridiagonal関数:

SciPyのeigh_tridiagonal関数を使用して、トリディアゴナル行列の固有値と固有ベクトルを求めます。
これらは波動関数と対応するエネルギー固有値です。

5. 波動関数のプロット:

最初の４つの基底状態の波動関数をforループで計算し、matplotlibを使用してそれらをグラフ化しています。
それぞれの波動関数は n = 1, 2, 3, 4 とラベル付けされており、量子調和振動子の波動関数の性質を示しています。

結果解説

[実行結果]

このグラフは、調和振動子ポテンシャルを持つシュレーディンガー方程式の基底状態の波動関数を表しています。

調和振動子ポテンシャルは、$ (\frac{1}{2}m\omega^2x^2) $と表され、量子力学で非常に重要なポテンシャルです。

プロットされた曲線は、それぞれの波動関数を表しています。
グラフの x 軸は位置を示し、y 軸は各波動関数の値を表しています。
波動関数は、量子力学における粒子の振る舞いを表現し、特定のエネルギー状態で粒子がどのように分布するかを示します。

この例では、最初の４つの基底状態の波動関数がプロットされています。
これらの波動関数は、それぞれ異なるエネルギー状態を表しており、基底状態から順に高次のエネルギー状態が表示されています。

波動関数はゼロ点振動（原点で振幅がゼロ）から始まり、対称性を持って左右に広がります。
それぞれの波動関数は異なる空間的な特性を持っており、基底状態から高次のエネルギー状態へとエネルギーが増加するにつれて、振動の幅が大きくなります。