ローレンツ方程式 SciPy

ローレンツ方程式

非線形微分方程式であるローレンツ方程式を解き、その結果を3次元のグラフで表示してみましょう。

ローレンツ系は次の3つの非線形連立微分方程式からなります。

$$
dx/dt = σ(y - x)
$$
$$
dy/dt = x(ρ - z) - y
$$
$$
dz/dt = xy - βz
$$

ここで、$σ、ρ、β$は正の定数です。

以下のPythonコードは、上記のローレンツ方程式を解き、その結果を3Dグラフで表示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def lorenz_system(current_state, t):
    sigma = 10.0 # σの値
    rho = 28.0 # ρの値
    beta = 8.0 / 3.0 # βの値

    x, y, z = current_state # 現在のx, y, zの値
    dx_dt = sigma * (y - x) # dx/dt
    dy_dt = x * (rho - z) - y # dy/dt
    dz_dt = x * y - beta * z # dz/dt

    return [dx_dt, dy_dt, dz_dt]

# 初期状態
initial_state = [1.0, 1.0, 1.0]

# 時間の範囲を定義
t = np.arange(0.0, 50.0, 0.01)

# 微分方程式を解く
solution = odeint(lorenz_system, initial_state, t)

# 結果を3Dグラフで表示
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.plot(solution[:, 0], solution[:, 1], solution[:, 2])
ax.set_title('Lorenz Attractor')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()

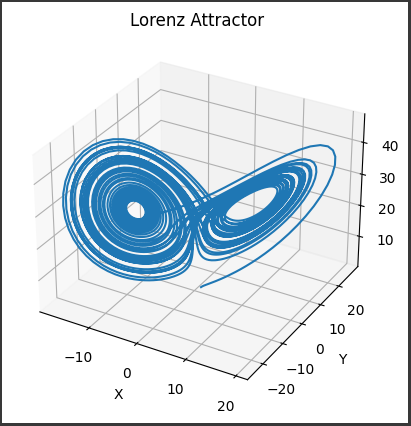
このコードを走らせると、解の軌道がローレンツアトラクターと呼ばれる蝶形の図形を形成します。

これはカオス理論を象徴する図形としてよく知られています。

[実行結果]

ソースコード解説

このコードは、ローレンツ方程式を数値的に解き、結果を3Dグラフとして表示するものです。

1. 必要なライブラリをインポートする:

numpy（数値計算のため）、scipy.integrateからのodeint（常微分方程式を解くため）、matplotlib.pyplot（グラフ描画のため）、mpl_toolkits.mplot3dからのAxes3D（3Dプロットのため）をインポートします。

2. ローレンツ方程式を定義する:

lorenz_system関数は、ローレンツ方程式を定義しています。
この方程式は3つの微分方程式からなり、特定のパラメータ（sigma、rho、beta）と現在の状態（x、y、z）を受け取ります。

それぞれの微分方程式は次のように表されます。
$$
dx/dt = sigma * (y - x)
$$
$$
dy/dt = x * (rho - z) - y
$$
$$
dz/dt = x * y - beta * z
$$

3. 初期状態を設定する:

initial_stateは、$x、y、z$の初期値を$1.0$として設定します。

4. 時間の範囲を定義する:

tは$0$から$50$までの時間の範囲を$0.01$刻みで定義します。

5. 微分方程式を解く:

odeint関数を使用して、lorenz_system関数に初期状態と時間の範囲を渡して微分方程式を解きます。

6. 結果を3Dグラフで表示する:

solutionは微分方程式の解です。
これを3Dグラフでプロットして、X、Y、Z軸に解の値をプロットし、Lorenz Attractorというタイトルをつけます。

これにより、ローレンツアトラクタとして知られる複雑な非線形系の挙動が視覚化されます。