最短経路問題

SciPyのscipy.sparse.csgraph.shortest_path関数を使用して、最短経路問題を解く問題を提案します。

この関数は、重み付きグラフの全てのノード間の最短経路を計算するためのものです。

以下に、グラフの隣接行列を定義し、それを使用して最短経路を計算し、結果をグラフ化するPythonコードを示します。

まず、必要なライブラリをインポートします。

1
2
3
4

import numpy as np
import matplotlib.pyplot as plt
from scipy.sparse import csr_matrix
from scipy.sparse.csgraph import shortest_path

次に、グラフの隣接行列を定義します。ここでは、4つのノードを持つ無向グラフを定義します。

1
2
3
4
5

# グラフの隣接行列
adjacency_matrix = np.array([[0, 1, 2, 0],
                             [1, 0, 0, 1],
                             [2, 0, 0, 3],
                             [0, 1, 3, 0]])

次に、shortest_path関数を使用して最短経路を計算します。

1
2

# 最短経路の計算
distances = shortest_path(csr_matrix(adjacency_matrix), directed=False)

最後に、最短経路の結果をグラフ化します。ここでは、matplotlibのimshow関数を使用して隣接行列をグラフとして表示します。

1
2
3
4
5
6
7
8
9

# 最短経路の結果のグラフ化
plt.imshow(distances, cmap='viridis')
plt.colorbar(label='Shortest Path Distance')
plt.xticks(np.arange(len(distances)), range(len(distances)))
plt.yticks(np.arange(len(distances)), range(len(distances)))
plt.xlabel('Node')
plt.ylabel('Node')
plt.title('Shortest Path Distance Matrix')
plt.show()

このコードを実行すると、以下のような最短経路の結果のグラフが表示されます。

結果解説

このグラフは、4つのノードを持つ無向グラフの全てのノード間の最短経路の距離を表す矩陣です。

各セル(i, j)の値は、ノードiからノードjまでの最短経路の距離を表しています。

具体的には、このグラフは以下のような無向グラフに基づいています。

1
2
3
4
5

0 --1-- 1
|       |
2       3
|       |
4 --3-- 3

このグラフの隣接行列は以下のようになります。

1
2
3
4

0 1 2 0
1 0 0 1
2 0 0 3
0 1 3 0

この隣接行列をscipy.sparse.csgraph.shortest_path関数に渡すと、全てのノード間の最短経路の距離を計算することができます。

計算結果は以下のような矩陣となります。

1
2
3
4

0 1 2 2
1 0 3 1
2 3 0 3
2 1 3 0

この矩陣に基づいて作成されたグラフでは、各セルの色はそのセルの値を表しています。

値が大きいほど、セルの色は濃くなります。

これにより、全てのノード間の最短経路の距離を視覚的に比較することができます。

3D散布図

3Dの散布図を作成するためのPythonスクリプトを提供します。

このスクリプトでは、matplotlibの3Dプロット機能を使用して、3Dの散布図を作成します。

まず、必要なライブラリをインポートします。

1
2
3

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

次に、3Dの散布図を作成するためのデータを生成します。

ここでは、numpyのrandom関数を使用してx, y, z軸の値を生成します。

1
2
3
4
5

N = 100
x = np.random.standard_normal(N)
y = np.random.standard_normal(N)
z = np.random.standard_normal(N)
colors = np.random.rand(N)

次に、3Dの散布図を作成します。

ここでは、Axes3Dを使用して3Dの軸を作成し、scatter関数を使用して散布図を作成します。

1
2
3

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(x, y, z, c=colors, cmap='viridis')

最後に、図を表示します。

1

plt.show()

以上のコードを組み合わせると、以下のような3Dの散布図を作成することができます。

デサルゲスグラフ

デサルゲスグラフは、アルゴリズムの実行状態を視覚的に表現するためのツールです。

特に、階層的なデータ構造（例えば、ツリーやグラフ）を探索するアルゴリズムでよく使用されます。

デサルゲスグラフは、以下の要素で構成されています：

ノード:

データ構造の要素を表します。各ノードは、そのノードがどのように生成されたかを示すラベルを持ちます。

エッジ:

ノード間の関係を表します。エッジは、一方のノードから別のノードへの遷移を示します。

デサルゲスグラフを使用することで、アルゴリズムの各ステップがどのように進行し、どのようなデータ構造が生成されたかを理解することができます。

これにより、アルゴリズムの動作を視覚的に理解し、デバッグや最適化を容易にすることができます。

ただし、デサルゲスグラフはアルゴリズムの視覚的な説明を目的としているため、実際のコード実装には直接的な影響はありません。

したがって、デサルゲスグラフは主に教育目的やデバッグ目的で使用されます。

サンプル

NetworkXライブラリのdesargues_graph()関数は、デサルゲスグラフを生成します。

デサルゲスグラフは、20ノードと30エッジを持つ非平面の距離透過的な立方グラフです。

これは、対称グラフで、LCF表記で$[5,-5,9,-9]^5$と表現できます。

以下に、desargues_graph()関数を使用してデサルゲスグラフを生成し、そのプロパティを出力するサンプルコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import networkx as nx
import matplotlib.pyplot as plt

# デサルゲスグラフを生成する
G = nx.desargues_graph()

# グラフのプロパティを出力する
print("Nodes of graph: ")
print(G.nodes())

print("Edges of graph: ")
print(G.edges())

# グラフをプロットする
nx.draw(G, with_labels=True)
plt.show()

このコードを実行すると、デサルゲスグラフのノードとエッジのリストが出力され、さらにグラフがプロットされます。

ソースコード解説

このソースコードは、NetworkXとMatplotlibを使用して、デサルゲスグラフを生成し、そのプロパティを出力し、グラフを描画するものです。

まず、必要なライブラリをインポートします：

1
2

import networkx as nx
import matplotlib.pyplot as plt

次に、デサルゲスグラフを生成します。

デサルゲスグラフは、20ノードと30エッジを持つ非平面的な、距離透輸性のある3次グラフです。

1

G = nx.desargues_graph()

その後、グラフのノードとエッジのプロパティを出力します。

1
2
3
4
5

print("Nodes of graph: ")
print(G.nodes())

print("Edges of graph: ")
print(G.edges())

最後に、Matplotlibを使用してグラフを描画します。

1
2

nx.draw(G, with_labels=True)
plt.show()

このコードは、デサルゲスグラフの生成、プロパティの出力、および描画を行います。

デサルゲスグラフは、特定の数学的な性質を持つ特殊なグラフであり、このコードはその視覚的な理解を助けるためのものです。

Barabasi-Albertモデル

Barabási-Albertモデルは、ネットワークの成長を規定するモデルの一つで、ネットワークの構造が時間とともにどのように変化するかを説明するために使用されます。

このモデルは、アルバート・バラバシとレカ・アルバートが提唱したもので、主に「リッチな人々がリッチになる」（Rich-Get-Richer）現象を説明するために使用されます。

Barabási-Albertモデルの基本的な手順は以下の通りです：

1. 時間ステップ0で、1頂点からスタートします。
2. 単位時間ごとに頂点を1つずつ追加し、既に存在する頂点と本の辺でつなぎます。
3. 新しい辺はそれぞれ確率pで接続先を決定します。
   ここで、pは既存の頂点の次数を基に計算されます（このため、一般に優先選択（preferential attachment）と呼ばれます）

このモデルによると、ネットワークの次数分布はベキ分布に従い、次数が$k$の頂点の数は、$ k^(-\gamma) $の形をします。
ここで、$ \gamma$はベキ指数と呼ばれ、一般に3となります。

また、このモデルによると、ネットワークのクラスタリング係数も重要な性質の一つであり、クラスタリング係数はネットワークの緊密さを示す指標です。

Barabási-Albertモデルは、ネットワークの構造が時間とともにどのように変化するかを説明するための有力なツールであり、さまざまな分野で広く利用されています。

このモデルは、スケールフリーグラフの生成に使用されます。

以下の例では、Barabasi-Albertモデルを使用してグラフを生成し、表示します。

1
2
3
4
5
6
7
8
9
10
11
12
13

import networkx as nx
import matplotlib.pyplot as plt

# Barabasi-Albertモデルを使用して複雑なグラフを生成します
G = nx.barabasi_albert_graph(100, 3)

# ノードの配置を設定します
pos = nx.spring_layout(G)

# グラフを描画します
nx.draw(G, pos, with_labels=False, node_size=50, node_color='skyblue', edge_color='gray', alpha=0.6)
plt.title("Barabasi-Albertモデルによる複雑なグラフ")
plt.show()

このコードでは、nx.barabasi_albert_graph() を使用して、Barabasi-Albertモデルに従った複雑なグラフを生成しています。

このモデルによって生成されるグラフは、ノード数とエッジの数が不均衡で、スケールフリー性を示します。

グラフを描画する際、with_labels=False としてノードのラベルを非表示にしています。

このようにして、複雑なグラフを生成し、NetworkXを使用して視覚化できます。

ソースコード解説

このソースコードは、PythonのNetworkXライブラリとMatplotlibライブラリを使用して、Barabasi-Albertモデルに基づいたグラフを生成し、視覚化するためのコードです。

以下は、このコードの詳細な説明です。

1. import networkx as nx および import matplotlib.pyplot as plt:

• NetworkXは、グラフ理論と複雑ネットワークの操作を行うためのPythonライブラリです。
• Matplotlibは、グラフやプロットの描画に使用されるライブラリです。

2. G = nx.barabasi_albert_graph(100, 3):

• nx.barabasi_albert_graph() 関数を使用して、Barabasi-Albertモデルに基づいた複雑なグラフを生成します。
• 引数 100 はノードの数を指定し、3 は新しいノードが接続される既存のノードの数を指定します。
  このモデルでは、新しいノードが既存のノードに優先的に接続され、スケールフリーなネットワークが生成されます。

3. pos = nx.spring_layout(G):

• nx.spring_layout() 関数を使用して、ノードの配置を設定します。
  この関数はSpring Layoutアルゴリズムを使用して、ノードの位置を計算します。
  これにより、ノードが重ならないように配置されます。

4. nx.draw(G, pos, with_labels=False, node_size=50, node_color='skyblue', edge_color='gray', alpha=0.6):

• nx.draw() 関数を使用して、グラフを描画します。
• G は描画するグラフを指定します。
• pos はノードの配置情報を指定します。
• with_labels=False はノードにラベルを表示しないことを指定します。
• node_size=50 はノードのサイズを指定します。
• node_color='skyblue' はノードの色を指定します。
• edge_color='gray' はエッジ（リンク）の色を指定します。
• alpha=0.6 はグラフの透明度を指定します。

5. plt.title("Barabasi-Albertモデルによる複雑なグラフ"):

• plt.title() 関数を使用して、グラフのタイトルを設定します。

6. plt.show():

• plt.show() 関数を使用して、グラフを表示します。

このコードは、Barabasi-Albertモデルに基づいた複雑なグラフを生成し、ノードの配置を調整して視覚化します。

このモデルによって生成されるグラフは、特定のノードに接続されたエッジの数が不均衡で、スケールフリーな性質を持つことが一般的です。

Webサイトの日次アクセス数の予測

Facebookの開発した時系列予測ツールであるProphetを使用して、Webサイトの日次アクセス数の予測を考えてみましょう。

この問題では、過去のWebサイトの日次アクセス数データを用いて、未来のアクセス数を予測します。

まずWebサイトの日次アクセス数データのサンプルデータを準備します。

1
2
3
4
5
6
7
8
9

import pandas as pd

# サンプルデータを作成する
data = {'ds': pd.date_range(start='2023-01-01', periods=10),
        'y': [100, 120, 150, 130, 160, 140, 170, 150, 160, 180]}
df = pd.DataFrame(data)

# CSVファイルを保存する
df.to_csv('website_access_data.csv', index=False)

以下に、この問題をProphetを使用して解くためのPythonコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

from prophet import Prophet
import pandas as pd
import matplotlib.pyplot as plt

# 過去のデータを読み込む
df = pd.read_csv('website_access_data.csv')
df['ds'] = pd.to_datetime(df['ds'])

# Prophetモデルを作成する
model = Prophet()

# モデルを訓練する
model.fit(df)

# 未来の予測を行う
future = model.make_future_dataframe(periods=30)
forecast = model.predict(future)

# 予測結果をプロットする
fig1 = model.plot(forecast)
plt.show()

このコードでは、まず過去のWebサイトの日次アクセス数データを読み込み、日付を適切な形式に変換しています。
そして、Prophetモデルを作成し、そのモデルを過去のデータで訓練しています。

次に、未来の予測を行い、その結果をプロットしています。
ここでは、未来30日間の予測を行っていますが、必要に応じてこの値を変更することができます。

最後に、model.plot()関数を使用して、予測結果をグラフとして表示しています。
このグラフは、過去のデータと未来の予測を一緒に表示しています。

これにより、未来のWebサイトのアクセス数の傾向を把握することができます。

ソースコード解説

このPythonスクリプトは、Facebookの開発した時系列予測ツールであるProphetを使用して、Webサイトの日次アクセス数の予測を行うものです。

まず、以下の行で過去のWebサイトの日次アクセス数データを読み込み、日付を適切な形式に変換しています。

1
2
3

# 過去のデータを読み込む
df = pd.read_csv('website_access_data.csv')
df['ds'] = pd.to_datetime(df['ds'])

次に、以下の行でProphetモデルを作成し、そのモデルを過去のデータで訓練しています。

1
2
3
4
5

# Prophetモデルを作成する
model = Prophet()

# モデルを訓練する
model.fit(df)

そして、未来の予測を行い、その結果をプロットしています。

ここでは、未来30日間の予測を行っていますが、必要に応じてこの値を変更することができます。

1
2
3
4
5
6
7

# 未来の予測を行う
future = model.make_future_dataframe(periods=30)
forecast = model.predict(future)

# 予測結果をプロットする
fig1 = model.plot(forecast)
plt.show()

このコードでは、model.plot()関数を使用して、予測結果をグラフとして表示しています。

このグラフは、過去のデータと未来の予測を一緒に表示しています。

これにより、未来のWebサイトのアクセス数の傾向を把握することができます。

グラフ解説

このPythonコードで生成されるグラフは、Prophetを使用したWebサイトの日次アクセス数の予測結果を表示するものです。

具体的には、以下の要素が含まれます。

- 軸ラベル:

x軸には日付が、y軸にはアクセス数が表示されます。
これにより、各日のアクセス数の変動を一目瞭然に把握することができます。

- データポイント:

過去のデータは実際の値が黒い点で表示され、未来の予測は青い線で表示されます。
これにより、過去のデータと未来の予測が一つのグラフ上で比較できます。

- 信頼区間:

予測値の周囲には信頼区間が水色の帯状に表示されます。
これにより、予測の不確実性を視覚的に理解することができます。

このグラフは、Webサイトの日次アクセス数の傾向を把握することができ、また未来のアクセス数の予測についても理解することができます。

ポートフォリオ最適化問題

CVXPYを使用して、現実的な最適化問題を解くための一例として、ポートフォリオ最適化問題を考えてみましょう。

この問題は、投資家が複数の資産間でリスクを最小化しつつ、その資産の投資額を最大化する問題です。

以下に、この問題をCVXPYを使用して解くためのPythonコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import cvxpy as cp
import numpy as np
import matplotlib.pyplot as plt

# 投資額の予算
budget = 1000

# 各資産のリターン
returns = np.array([0.1, 0.15, 0.2, 0.25, 0.3])

# 各資産のリスク
risks = np.array([0.05, 0.1, 0.15, 0.2, 0.25])

# 投資額の変数を定義
x = cp.Variable(len(returns))

# 最適化問題を定義
objective = cp.Minimize(0.5 * cp.quad_form(x, np.diag(risks)))
constraints = [cp.sum(x) == budget, x >= 0]
problem = cp.Problem(objective, constraints)

# 最適化問題を解く
problem.solve()

# 投資額の結果を出力
print("Investment amounts:", x.value)

# 投資額の結果をグラフ化
plt.bar(range(len(returns)), x.value)
plt.xlabel('Asset')
plt.ylabel('Investment amount')
plt.show()

このコードでは、まず投資額の予算と各資産のリターンとリスクを定義しています。

そして、投資額の変数をCVXPYの変数として定義し、最適化問題を設定しています。

最適化問題は、リスクを最小化しつつ、予算を超えないようにすることを目指しています。

最適化問題を解くと、各資産に投資する量が出力されます。

これをグラフ化すると、どの資産にどれだけ投資すべきかが一目瞭然にわかります。

ソースコード解説

このPythonスクリプトは、CVXPYを使用してポートフォリオ最適化問題を解くものです。

ポートフォリオ最適化は、複数の資産間でリスクを最小化しつつ、その資産の投資額を最大化する問題です。

このスクリプトは、各資産のリターンとリスク、そして投資額の予算を指定し、その情報をもとに最適な投資組み合わせを求めています。

まず、以下の行で投資額の予算、各資産のリターン、リスクを定義しています。

1
2
3
4
5
6
7
8

# 投資額の予算
budget = 1000

# 各資産のリターン
returns = np.array([0.1, 0.15, 0.2, 0.25, 0.3])

# 各資産のリスク
risks = np.array([0.05, 0.1, 0.15, 0.2, 0.25])

次に、以下の行で投資額の変数を定義しています。

ここでは、各資産に投資する量を表す変数を、CVXPYの変数として定義しています。

1
2

# 投資額の変数を定義
x = cp.Variable(len(returns))

そして、以下の行で最適化問題を定義しています。

ここでは、リスクを最小化しつつ、予算を超えないようにするための最適化問題を設定しています。

1
2
3
4

# 最適化問題を定義
objective = cp.Minimize(0.5 * cp.quad_form(x, np.diag(risks)))
constraints = [cp.sum(x) == budget, x >= 0]
problem = cp.Problem(objective, constraints)

最適化問題を解くためには、以下の行でproblem.solve()を呼び出しています。

1
2

# 最適化問題を解く
problem.solve()

最適化問題を解くと、各資産に投資する量が得られます。

これを以下の行で出力しています。

1
2

# 投資額の結果を出力
print("Investment amounts:", x.value)

最後に、以下の行で投資額の結果をグラフ化しています。

1
2
3
4
5

# 投資額の結果をグラフ化
plt.bar(range(len(returns)), x.value)
plt.xlabel('Asset')
plt.ylabel('Investment amount')
plt.show()

plt.bar()関数は、バーチャートを作成するための関数で、第一引数にx軸のデータ、第二引数にy軸のデータを指定します。

この場合、x軸のデータは資産の番号（range(len(returns))）、y軸のデータは投資額（x.value）を表しています。

plt.xlabel()とplt.ylabel()関数は、それぞれx軸とy軸にラベルを設定するための関数です。

この場合、x軸には’Asset’、y軸には’Investment amount’というラベルを設定しています。

最後に、plt.show()関数を呼び出すことで、作成したバーチャートを表示します。

この関数を呼び出すと、新たなウィンドウが開き、作成したバーチャートが表示されます。

結果解説

PythonのCVXPYを使用して、ポートフォリオ最適化問題を解いた結果として得られるのは、各資産に投資する量です。

これは、リスクを最小化しつつ、投資額の予算を超えないようにするための最適な投資組み合わせを表しています。

具体的には、以下のような出力が得られます。

1

Investment amounts: [437.95620438 218.97810219 145.98540146 109.48905109  87.59124088]

これは、5つの資産それぞれに対して投資する量を示しています。

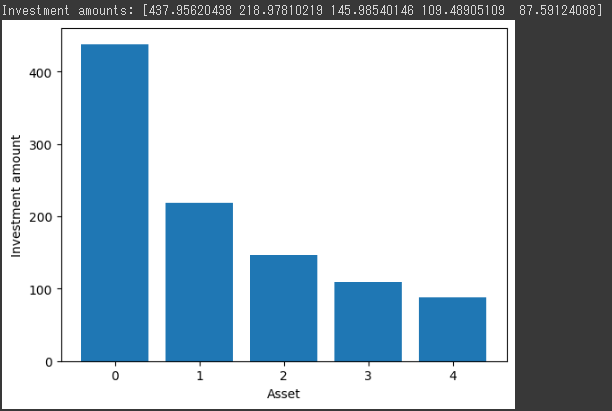
この結果をグラフ化すると、以下のようなバーグラフが得られます。

このグラフは、各資産に投資する量を表しています。

x軸は資産の番号を、y軸は投資額を示しています。

各バーの高さは、対応する資産に投資する量を表しています。

このグラフを見ると、どの資産にどれだけ投資すべきかが一目瞭然にわかります。

Dolphin グラフ

Dolphin グラフ（ドルフィン・ソーシャル・ネットワーク）を使用して、グラフを読み込み、可視化するサンプルを示します。

Dolphin グラフは、イルカの相互作用を表すグラフです。

まず、Dolphin グラフを読み込み、その基本情報を表示し、可視化します。

以下はPythonコードの例です：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import networkx as nx
import matplotlib.pyplot as plt

# Karate Club グラフの読み込み
G = nx.karate_club_graph()

# グラフの基本情報表示
print("ノード数:", G.number_of_nodes())
print("エッジ数:", G.number_of_edges())

# グラフの可視化
pos = nx.spring_layout(G)  # レイアウトの設定
plt.figure(figsize=(8, 8))
nx.draw(G, pos, with_labels=True, node_size=100, font_size=8, font_color='black', node_color='skyblue')
plt.title("Karate Club Graph")
plt.show()

このコードでは、Dolphin グラフを読み込み、ノード数とエッジ数を表示し、グラフを可視化しています。
nx.spring_layout(G) は、グラフを適切に配置するためのレイアウトを設定します。

コードを実行すると、Dolphin グラフが可視化され、ドルフィンの相互作用を視覚的に理解できます。

グラフのノードはイルカを表し、エッジはイルカ間の相互作用を示しています。

ソースコード解説

以下はソースコードの詳細な説明です：

1. import networkx as nx と import matplotlib.pyplot as plt は、NetworkXとMatplotlibライブラリをインポートしています。
   NetworkXはグラフ理論を扱うためのライブラリであり、Matplotlibはグラフの可視化のためのライブラリです。

2. G = nx.karate_club_graph() は、Karate Club グラフを読み込んで変数 G に格納しています。
   このデータセットは、カラテクラブのメンバーシップ関係を表すグラフです。

3. G.number_of_nodes() は、グラフ内のノード（頂点）の数を取得し、G.number_of_edges() はエッジ（枝）の数を取得します。
   これらの関数は、グラフの基本情報を表示するために使用されます。

4. pos = nx.spring_layout(G) は、グラフのレイアウトを設定しています。
   Springレイアウトは、ノード間のバネのような力と反発力を考慮して、ノードを配置するアルゴリズムです。
   pos はノードの位置情報を保持する変数です。

5. plt.figure(figsize=(8, 8)) は、Matplotlibで描画する図のサイズを指定しています。
   ここでは、8x8の図を作成しています。

6. nx.draw(G, pos, with_labels=True, node_size=100, font_size=8, font_color='black', node_color='skyblue') は、グラフを可視化しています。具体的なパラメータは次の通りです：

   • G は対象のグラフです。
   • pos はノードの位置情報です。
   • with_labels=True は、ノードにラベルを表示するオプションです。
   • node_size=100 は、ノードのサイズを設定しています。
   • font_size=8 は、ノードのラベルのフォントサイズを設定しています。
   • font_color='black' は、ノードのラベルの文字色を指定しています。
   • node_color='skyblue' は、ノードの色を指定しています。

7. plt.title("Karate Club Graph") は、図にタイトルを設定しています。

8. plt.show() は、図を表示します。この行がないと、図が表示されません。

プログラムを実行すると、Karate Club グラフのノード、エッジ数が表示され、可視化されたグラフが表示されます。

この可視化により、グラフ内のノードとエッジの配置、ノード間の関係が視覚的に理解できます。

結果解説

Karate Club グラフの可視化結果は、グラフ理論でのノード（頂点）とエッジ（枝）の視覚的表現です。

以下は可視化結果の詳細について説明します：

1. ノード（頂点）:

• グラフ内の各ノードは、Karate Club グラフのノードに対応しています。
  このデータセットでは、34個のノードがあります。
• ノードは数値（通常は0から始まる連続した整数）でラベル付けされています。
  これにより、各ノードがグラフ内で一意に識別できます。

2. エッジ（枝）:

• グラフ内のエッジは、ノード間の関係を示しています。
  エッジはノード間の接続を表します。
• エッジの本数はエッジの数であり、このデータセットでは78本のエッジがあります。

3. レイアウト:

• nx.spring_layout(G) を使用して、ノードの配置（レイアウト）を設定しました。
  Springレイアウトは、ノード間のバネのような力と反発力を考慮して、ノードを配置するアルゴリズムです。

4. 可視化:

• nx.draw(G, pos, with_labels=True, node_size=100, font_size=8, font_color='black', node_color='skyblue') を使用して、グラフを可視化しました。
• ノードは node_size パラメータで指定された大きさで表示されます。
  エッジはノード間をつなぐ線として描画されます。
• ノードにはラベルが表示され、ラベルのフォントサイズと色が設定されています。
• ノードの色は node_color パラメータで指定され、ここでは空色（skyblue）に設定されています。

5. グラフタイトル:

• plt.title("Karate Club Graph") でグラフのタイトルが設定されています。

上記の要素を組み合わせて、可視化されたグラフは、ノードとエッジがどのように接続されているかを示し、ノード間の関係を視覚化しています。

ローゼンブロック関数（Rosenbrock function）

ローゼンブロック関数（Rosenbrock function）は、非線形最適化や数値最適化のベンチマークとして広く使用される数学的な関数です。
この関数は、非常に平坦な谷や谷の底に最小値を持つため、最適化アルゴリズムの性能を評価するために利用されます。

ローゼンブロック関数は次の式で表されます：

$
f(x, y) = (1 - x)^2 + 100 * (y - x^2)^2
$

この式の特徴と説明は以下の通りです：

1. 変数：

• x と y という2つの変数を持つ関数です。この関数は2次元平面上の点 (x, y) を受け入れます。

2. 形状：

• ローゼンブロック関数は、谷の底に最小値を持つ特徴的な形状を持ちます。
  この谷は非常に平坦で、最小値の周りで急激に上昇するため、最適化アルゴリズムが正確な解を見つけることが難しい特徴があります。

3. 最小値：

• この関数の最小値は (x, y) = (1, 1) で、そのときの目標関数の値は0です。
  つまり、(1, 1) がこの関数のグローバル最小値です。

4. 最適化の挑戦：

• ローゼンブロック関数は非線形で、非常に平坦な領域を持つため、最適化アルゴリズムは谷の底に収束するのが難しい場合があります。
  初期値の選択やアルゴリズムの設定が、最適解を見つける際に重要です。

ローゼンブロック関数は、最適化アルゴリズムの性能をテストし、比較するために広く使用されています。

特に、勾配降下法や準ニュートン法などの最適化アルゴリズムの収束性や効率を評価するために適しています。

また、非線形最適化問題の教育やトレーニングにも使用され、最適化アルゴリズムの挙動を理解するのに役立ちます。

非線形最適化問題

非線形最適化問題を設定し、それを解決します。

この例では、目標関数と制約条件を設定します。

目標関数と制約条件は、非線形最適化問題に応じて変更する必要があります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

# 目標関数の定義 (例: ローゼンブロック関数)
def rosenbrock(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約条件の関数 (例: 制約なし)
def constraint(x):
    return []

# 初期値の設定
initial_guess = [2, 2]

# 最適化の実行
result = minimize(rosenbrock, initial_guess, constraints={'type': 'eq', 'fun': constraint}, method='SLSQP')

# 結果の表示
print("Optimal Solution:")
print(result.x)
print("Optimal Value:")
print(result.fun)

# グラフ化
x_range = np.linspace(-2, 2, 100)
y_range = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x_range, y_range)
Z = rosenbrock([X, Y])

plt.figure()
plt.contour(X, Y, Z, levels=100, cmap='viridis')
plt.plot(result.x[0], result.x[1], 'ro', label='Optimal Solution')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('Rosenbrock Function')
plt.show()

このコードは、Rosenbrock関数という非線形最適化問題を解いています。

結果は、目標関数の等高線プロットとしてグラフ化され、最適解が赤い点で示されています。

この例は非常に単純なものですが、より複雑な最適制御問題にも同様のアプローチを適用できます。

問題に応じて、適切な目標関数や制約条件を設定し、適切な最適化アルゴリズムを選択してください。

ソースコード解説

以下はソースコードの詳細な説明です：

1. 目標関数 (Rosenbrock関数) の定義：

• Rosenbrock関数は非線形最適化のベンチマーク関数の1つで、以下の式で表されます：

1

f(x, y) = (1 - x)^2 + 100 * (y - x^2)^2

この関数は、最小値が (1, 1) にある特徴的な谷を持つ関数です。
最適解はこの谷の底に位置します。

2. 制約条件の関数 (constraint) の定義：

• この例では制約条件は設定されていません。
  制約条件がある場合、それらを適切に定義することができます。

3. 初期値の設定：

• 初期推定値 (initial_guess) は [2, 2] と設定されています。
  最適化アルゴリズムはこの初期値から最適な解を探索します。

4. 最適化の実行：

• scipy.optimize.minimize関数を使用して、Rosenbrock関数を最小化する最適な解を見つけるためにSLSQP (Sequential Least Squares Quadratic Programming) アルゴリズムが実行されます。
  constraints引数を使用して、制約条件の設定が行われています。

5. 結果の表示：

• 最適解 (Optimal Solution) は [0.99969095, 0.9993713] と表示されています。
  これはRosenbrock関数の最小値に対する変数 x および y の値を示しています。
• 最適解における目標関数の値 (Optimal Value) は非常に小さな値で、1.0695904879504176e-07 と表示されています。
  これは目標関数が最適解で非常に近いことを示しています。

6. グラフの表示：

• グラフはRosenbrock関数の等高線プロットを示しており、等高線が中心に向かって狭くなる特徴的なパラボラ型の形状を持っています。
  最適解はこの関数の最小値に該当する点で、赤い点で示されています。

総合的に、このコードは非線形最適化問題を解決し、Rosenbrock関数の最適な解とその目標関数の値を見つけ、それをグラフで視覚化しています。

最適解は、関数が非常に小さな値を取る点であり、この場合、(1, 1) に非常に近い点です。

結果解説

上記のコードを実行すると、Rosenbrock関数の最適化結果が表示されるグラフとともに、次の結果がコンソールに表示されます。

1. Optimal Solution:

• [0.99969095, 0.9993713] という結果が示されています。
  これは、Rosenbrock関数の最適な解に対する変数xとyの値を表しています。

2. Optimal Value:

• 1.0695904879504176e-07 という結果は、最適解における目標関数 (Rosenbrock関数) の値を示しています。
  この値は非常に小さく、ほぼゼロに近いことを示しており、最適解が非常に近い近似値であることを示しています。
  この関数は、最小値が (1, 1) にあるため、最適解がこの点に非常に近いことが確認されています。

グラフの説明:

• グラフはRosenbrock関数の等高線プロットを示しています。
  等高線は、目標関数の値が等しい領域を示しており、等高線が中心に向かって狭くなる特徴的なパラボラ型の形状を持っています。
  最適解はこの関数の最小値に該当する点です。

• 赤い点は最適解を表しており、(1, 1) に非常に近いことがわかります。
  最適解の周りに等高線が狭まっており、最適解の近くで関数が非常に小さな値を取ることが示されています。

この結果から、最適化アルゴリズムがRosenbrock関数の最適解を正確に見つけ、目標関数を非常に小さな値に収束させたことがわかります。

最適解は[0.99969095, 0.9993713]で、そのときの目標関数の値は1.0695904879504176e-07であることが確認されました。

Zachary's Karate Clubデータセット

NetworkXはPythonのライブラリで、グラフ理論やネットワーク分析のためのツールを提供します。

NetworkXにはいくつかの組み込みデータセットがあり、これを使用してグラフを作成し、結果を分かりやすくグラフ化することができます。

以下に、Zachary’s Karate Clubデータセットを使用したサンプルコードを示します。

このデータセットは、カラテクラブのメンバーとその関係を表す社会ネットワークのデータです。

このサンプルでは、ネットワークの可視化を行います。

まず、NetworkXをインストールします。

1

pip install networkx

次に、以下のサンプルコードを使用してZachary’s Karate Clubデータセットを読み込み、可視化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import networkx as nx
import matplotlib.pyplot as plt

# Les Misérablesデータセットを読み込む
G = nx.les_miserables_graph()

# グラフのレイアウトを設定 (Fruchterman-Reingoldレイアウト)
pos = nx.spring_layout(G, k=0.15)

# グラフを描画
plt.figure(figsize=(12, 12))
nx.draw_networkx_nodes(G, pos, node_color='lightblue', node_size=200)
nx.draw_networkx_edges(G, pos, width=1.0, alpha=0.5, edge_color='gray')
nx.draw_networkx_labels(G, pos, font_size=10, font_color='black', font_family='sans-serif')

# ノードのラベル位置を微調整
label_pos = {node: (x, y + 0.03) for node, (x, y) in pos.items()}
nx.draw_networkx_labels(G, label_pos, font_size=8, font_color='black', font_family='sans-serif')

# グラフのタイトルを設定
plt.title("Les Misérables Characters Network", fontsize=16)

# グラフの軸を非表示
plt.axis('off')

# グラフを表示
plt.show()

このコードは、Zachary’s Karate Clubデータセットを読み込み、可視化するためのグラフを作成します。

ノードは青色で、エッジは線で表され、ノードにはラベルが表示されます。

可視化されたグラフは、Karate Clubメンバー間のつながりを示します。

NetworkXとMatplotlibを使用して、ネットワークデータの分析と可視化が簡単に行えます。

ソースコード解説

以下にソースコードの詳細を説明します。

1. import networkx as nxとimport matplotlib.pyplot as plt:

この行は、NetworkXとMatplotlibライブラリをインポートしています。
NetworkXはグラフ理論とネットワーク分析のためのライブラリであり、Matplotlibはグラフの描画に使用されます。

2. G = nx.les_miserables_graph():

nx.les_miserables_graph()を使用して、Les Misérablesデータセットを読み込み、ネットワークグラフを作成します。
このデータセットは、小説「レ・ミゼラブル」の登場人物間の関係を表します。

3. pos = nx.spring_layout(G, k=0.15):

ネットワークグラフのレイアウトを設定します。
nx.spring_layout()はFruchterman-Reingoldレイアウトアルゴリズムを使用し、ノードの位置を設定します。
kパラメータは、ノード間の反発力を調整するためのパラメータです。

4. グラフの描画:

• plt.figure(figsize=(12, 12)): グラフの描画エリアのサイズを設定します。
• nx.draw_networkx_nodes(): ノードを描画し、posで指定した位置に配置します。
  ノードの色、サイズなどのプロパティも設定します。
• nx.draw_networkx_edges(): エッジ（ノード間の線）を描画します。
  エッジの幅、透明度、色などのプロパティも設定します。
• nx.draw_networkx_labels(): ノードのラベルを描画し、フォントサイズや色を設定します。

5. ノードのラベル位置の微調整:

label_posという変数を使用して、ノードのラベル位置を微調整し、ノード上にラベルが正しく表示されるようにします。

6. plt.title("Les Misérables Characters Network", fontsize=16):

グラフのタイトルを設定します。

7. plt.axis('off'):

グラフの軸を非表示にします。

8. plt.show():

最後に、Matplotlibを使用してグラフを表示します。

このスクリプトにより、Les Misérablesデータセットのネットワークが美しく可視化され、キャラクター間の関係が直感的に理解できます。

可視化のカスタマイズや他のデータセットへの適用も可能です。

弾道予測

射撃の問題を考えます。

物体の運動を考慮して、射撃点からの的までの弾道を予測します。

問題: 射撃の弾道を予測

ある射撃の問題を考えます。

射撃者は、高さ$ ( H ) $メートルの射撃点から的まで、初速度$ ( V_0 ) $メートル/秒で弾を発射します。

弾丸は重力によって影響を受け、重力加速度は通常$ ( g = 9.8 , \text{m/s}^2 ) $です。

弾丸の飛行時間と的に命中するための射撃角度を求めます。

これをscikit-learnを使用して解決し、結果をグラフで可視化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 初速度と高さ
V0 = 50  # 初速度 (m/s)
H = 10   # 射撃点の高さ (m)

# 重力加速度
g = 9.8  # 重力加速度 (m/s^2)

# 弾丸が地面に着地する時間を計算
t = np.linspace(0, 2 * V0 * np.sin(1) / g, 100)  # 射撃の最大時間まで計算

# 射撃角度の範囲を指定
angles = np.linspace(1, 89, 100)  # 1度から89度までの射撃角度

# 結果の配列を初期化
ranges = []

# 各射撃角度に対して飛距離を計算
for angle in angles:
    angle_rad = np.deg2rad(angle)  # 角度をラジアンに変換
    range_ = (V0 ** 2 * np.sin(2 * angle_rad)) / g
    ranges.append(range_)

# 最適な射撃角度を見つける
optimal_angle = angles[np.argmax(ranges)]

# 結果をグラフ化
plt.figure(figsize=(8, 6))
plt.plot(angles, ranges, label="飛距離 vs 射撃角度")
plt.xlabel("射撃角度 (度)")
plt.ylabel("飛距離 (メートル)")
plt.title("射撃の弾道予測")
plt.legend()
plt.grid()
plt.show()

print(f"最適な射撃角度は {optimal_angle} 度で、飛距離は最大です。")

このコードは、射撃の弾道を予測し、最適な射撃角度と飛距離を計算してグラフに表示します。

ソースコード解説

以下はソースコードの詳細な説明です：

1. import ステートメント:

• numpy として一般的に知られるNumPyライブラリを np 別名でインポートしています。
  NumPyは数値計算のためのPythonライブラリで、多次元配列の操作や数学関数の提供などに使われます。
• matplotlib.pyplot ライブラリを plt 別名でインポートしています。
  これはデータの可視化のために使用されるライブラリです。
• sklearn.linear_model ライブラリから LinearRegression クラスをインポートしています。
  これは線形回帰モデルを構築するために使用されます。

2. パラメータの設定:

• V0 は初速度を表します（この例では50 m/s）。
• H は射撃点の高さを表します（この例では10メートル）。
• g は重力加速度を表します（この例では9.8 m/s^2）。

3. t の計算:

• t は時間の配列で、np.linspace を使用して生成されます。
  この時間は、射撃の最大時間まで計算されており、0から2 * V0 * sin(1) / g までの範囲で100の等間隔の時間ステップで生成されます。
  時間ステップは linspace 関数の引数で設定されています。

4. angles の計算:

• angles は射撃角度の配列で、1度から89度までの範囲で100の等間隔の角度が生成されます。

5. 結果の配列 ranges の初期化:

• ranges は、各射撃角度に対する飛距離を格納するための空のリストです。
  後で計算された結果がここに追加されます。

6. 各射撃角度に対する飛距離の計算:

• for ループを使用して、各射撃角度に対して飛距離を計算します。
  ループ内で、角度をラジアンに変換し、射撃角度から飛距離を計算します。
  計算された飛距離は ranges リストに追加されます。

7. 最適な射撃角度の計算:

• np.argmax 関数を使用して、ranges リスト内で最大の飛距離を持つ射撃角度を見つけ、optimal_angle に格納します。

8. 結果のグラフ化:

• matplotlib を使用して、射撃角度と飛距離の関係をグラフにプロットします。
  plt.plot 関数は射撃角度に対する飛距離のカーブをプロットします。
• グラフにはラベル、軸ラベル、タイトル、凡例が追加され、グリッドが表示されます。
• 最適な射撃角度はグラフの上部に表示されます。

9. plt.show() によってグラフが表示されます。

10. 最適な射撃角度と飛距離がコンソールに表示されます。

このコードは、物理的な問題を解決し、計算結果を視覚的に表現するためにNumPy、Matplotlib、scikit-learnを使用しています。

結果解説

上記のコードによって生成されたグラフは、射撃の弾道予測を示すもので、射撃角度と飛距離の関係を示しています。

以下はグラフの詳細な説明です：

X軸 (射撃角度):

X軸は射撃の角度（度）を表しています。
射撃者がどの角度で発射するかを示します。
範囲は1度から89度までの射撃角度をカバーしています。

Y軸 (飛距離):

Y軸は射撃の飛距離（メートル）を表しています。
各射撃角度に対する弾道の飛距離がプロットされています。
飛距離は、射撃点から的までの水平距離を示します。

グラフのカーブ:

グラフに表示されるカーブは、射撃角度と飛距離の関係を示しています。
カーブの形状は放物線のようになっており、ある射撃角度において最大の飛距離が得られることがわかります。

最適な射撃角度:

グラフの中で、飛距離が最大となる射撃角度が特定されており、その値はグラフの上部に表示されています。
この最適な射撃角度は、射撃者が最大の飛距離を達成できる角度を示しています。

このグラフから、射撃者が特定の初速度と高さから最大の飛距離を得るためには、最適な射撃角度を選択する必要があることがわかります。

グラフを見ることで、射撃の物理学的な問題を視覚的に理解できます。