弾道予測 scikit-learn

弾道予測

射撃の問題を考えます。

物体の運動を考慮して、射撃点からの的までの弾道を予測します。

問題: 射撃の弾道を予測

ある射撃の問題を考えます。

射撃者は、高さ$ ( H ) $メートルの射撃点から的まで、初速度$ ( V_0 ) $メートル/秒で弾を発射します。

弾丸は重力によって影響を受け、重力加速度は通常$ ( g = 9.8 , \text{m/s}^2 ) $です。

弾丸の飛行時間と的に命中するための射撃角度を求めます。

これをscikit-learnを使用して解決し、結果をグラフで可視化します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

# 初速度と高さ
V0 = 50  # 初速度 (m/s)
H = 10   # 射撃点の高さ (m)

# 重力加速度
g = 9.8  # 重力加速度 (m/s^2)

# 弾丸が地面に着地する時間を計算
t = np.linspace(0, 2 * V0 * np.sin(1) / g, 100)  # 射撃の最大時間まで計算

# 射撃角度の範囲を指定
angles = np.linspace(1, 89, 100)  # 1度から89度までの射撃角度

# 結果の配列を初期化
ranges = []

# 各射撃角度に対して飛距離を計算
for angle in angles:
    angle_rad = np.deg2rad(angle)  # 角度をラジアンに変換
    range_ = (V0 ** 2 * np.sin(2 * angle_rad)) / g
    ranges.append(range_)

# 最適な射撃角度を見つける
optimal_angle = angles[np.argmax(ranges)]

# 結果をグラフ化
plt.figure(figsize=(8, 6))
plt.plot(angles, ranges, label="飛距離 vs 射撃角度")
plt.xlabel("射撃角度 (度)")
plt.ylabel("飛距離 (メートル)")
plt.title("射撃の弾道予測")
plt.legend()
plt.grid()
plt.show()

print(f"最適な射撃角度は {optimal_angle} 度で、飛距離は最大です。")

このコードは、射撃の弾道を予測し、最適な射撃角度と飛距離を計算してグラフに表示します。

ソースコード解説

以下はソースコードの詳細な説明です：

1. import ステートメント:

  • numpy として一般的に知られるNumPyライブラリを np 別名でインポートしています。
    NumPyは数値計算のためのPythonライブラリで、多次元配列の操作や数学関数の提供などに使われます。
  • matplotlib.pyplot ライブラリを plt 別名でインポートしています。
    これはデータの可視化のために使用されるライブラリです。
  • sklearn.linear_model ライブラリから LinearRegression クラスをインポートしています。
    これは線形回帰モデルを構築するために使用されます。

2. パラメータの設定:

  • V0 は初速度を表します（この例では50 m/s）。
  • H は射撃点の高さを表します（この例では10メートル）。
  • g は重力加速度を表します（この例では9.8 m/s^2）。

3. t の計算:

  • t は時間の配列で、np.linspace を使用して生成されます。
    この時間は、射撃の最大時間まで計算されており、0から2 * V0 * sin(1) / g までの範囲で100の等間隔の時間ステップで生成されます。
    時間ステップは linspace 関数の引数で設定されています。

4. angles の計算:

  • angles は射撃角度の配列で、1度から89度までの範囲で100の等間隔の角度が生成されます。

5. 結果の配列 ranges の初期化:

  • ranges は、各射撃角度に対する飛距離を格納するための空のリストです。
    後で計算された結果がここに追加されます。

6. 各射撃角度に対する飛距離の計算:

  • for ループを使用して、各射撃角度に対して飛距離を計算します。
    ループ内で、角度をラジアンに変換し、射撃角度から飛距離を計算します。
    計算された飛距離は ranges リストに追加されます。

7. 最適な射撃角度の計算:

  • np.argmax 関数を使用して、ranges リスト内で最大の飛距離を持つ射撃角度を見つけ、optimal_angle に格納します。

8. 結果のグラフ化:

  • matplotlib を使用して、射撃角度と飛距離の関係をグラフにプロットします。
    plt.plot 関数は射撃角度に対する飛距離のカーブをプロットします。
  • グラフにはラベル、軸ラベル、タイトル、凡例が追加され、グリッドが表示されます。
  • 最適な射撃角度はグラフの上部に表示されます。

9. plt.show() によってグラフが表示されます。

10. 最適な射撃角度と飛距離がコンソールに表示されます。

このコードは、物理的な問題を解決し、計算結果を視覚的に表現するためにNumPy、Matplotlib、scikit-learnを使用しています。

結果解説

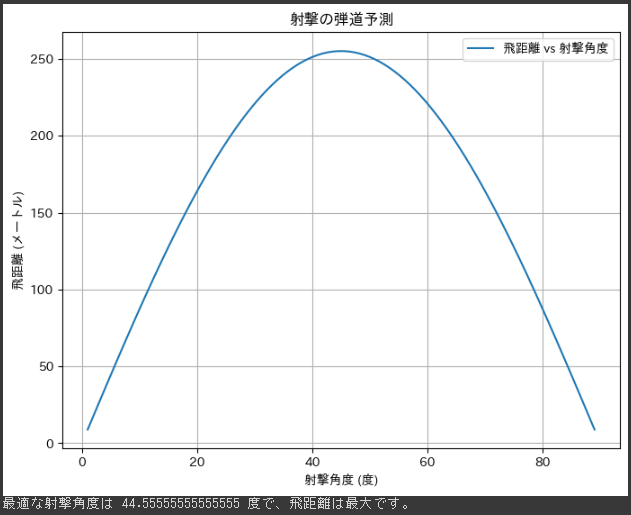
上記のコードによって生成されたグラフは、射撃の弾道予測を示すもので、射撃角度と飛距離の関係を示しています。

以下はグラフの詳細な説明です：

X軸 (射撃角度):

X軸は射撃の角度（度）を表しています。
射撃者がどの角度で発射するかを示します。
範囲は1度から89度までの射撃角度をカバーしています。

Y軸 (飛距離):

Y軸は射撃の飛距離（メートル）を表しています。
各射撃角度に対する弾道の飛距離がプロットされています。
飛距離は、射撃点から的までの水平距離を示します。

グラフのカーブ:

グラフに表示されるカーブは、射撃角度と飛距離の関係を示しています。
カーブの形状は放物線のようになっており、ある射撃角度において最大の飛距離が得られることがわかります。

最適な射撃角度:

グラフの中で、飛距離が最大となる射撃角度が特定されており、その値はグラフの上部に表示されています。
この最適な射撃角度は、射撃者が最大の飛距離を達成できる角度を示しています。

このグラフから、射撃者が特定の初速度と高さから最大の飛距離を得るためには、最適な射撃角度を選択する必要があることがわかります。

グラフを見ることで、射撃の物理学的な問題を視覚的に理解できます。