ローゼンブロック関数（Rosenbrock function） SciPy

ローゼンブロック関数（Rosenbrock function）

ローゼンブロック関数（Rosenbrock function）は、非線形最適化や数値最適化のベンチマークとして広く使用される数学的な関数です。
この関数は、非常に平坦な谷や谷の底に最小値を持つため、最適化アルゴリズムの性能を評価するために利用されます。

ローゼンブロック関数は次の式で表されます：

$
f(x, y) = (1 - x)^2 + 100 * (y - x^2)^2
$

この式の特徴と説明は以下の通りです：

1. 変数：

  • x と y という2つの変数を持つ関数です。この関数は2次元平面上の点 (x, y) を受け入れます。

2. 形状：

  • ローゼンブロック関数は、谷の底に最小値を持つ特徴的な形状を持ちます。
    この谷は非常に平坦で、最小値の周りで急激に上昇するため、最適化アルゴリズムが正確な解を見つけることが難しい特徴があります。

3. 最小値：

  • この関数の最小値は (x, y) = (1, 1) で、そのときの目標関数の値は0です。
    つまり、(1, 1) がこの関数のグローバル最小値です。

4. 最適化の挑戦：

  • ローゼンブロック関数は非線形で、非常に平坦な領域を持つため、最適化アルゴリズムは谷の底に収束するのが難しい場合があります。
    初期値の選択やアルゴリズムの設定が、最適解を見つける際に重要です。

ローゼンブロック関数は、最適化アルゴリズムの性能をテストし、比較するために広く使用されています。

特に、勾配降下法や準ニュートン法などの最適化アルゴリズムの収束性や効率を評価するために適しています。

また、非線形最適化問題の教育やトレーニングにも使用され、最適化アルゴリズムの挙動を理解するのに役立ちます。

非線形最適化問題

非線形最適化問題を設定し、それを解決します。

この例では、目標関数と制約条件を設定します。

目標関数と制約条件は、非線形最適化問題に応じて変更する必要があります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt

# 目標関数の定義 (例: ローゼンブロック関数)
def rosenbrock(x):
    return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2

# 制約条件の関数 (例: 制約なし)
def constraint(x):
    return []

# 初期値の設定
initial_guess = [2, 2]

# 最適化の実行
result = minimize(rosenbrock, initial_guess, constraints={'type': 'eq', 'fun': constraint}, method='SLSQP')

# 結果の表示
print("Optimal Solution:")
print(result.x)
print("Optimal Value:")
print(result.fun)

# グラフ化
x_range = np.linspace(-2, 2, 100)
y_range = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x_range, y_range)
Z = rosenbrock([X, Y])

plt.figure()
plt.contour(X, Y, Z, levels=100, cmap='viridis')
plt.plot(result.x[0], result.x[1], 'ro', label='Optimal Solution')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.title('Rosenbrock Function')
plt.show()

このコードは、Rosenbrock関数という非線形最適化問題を解いています。

結果は、目標関数の等高線プロットとしてグラフ化され、最適解が赤い点で示されています。

この例は非常に単純なものですが、より複雑な最適制御問題にも同様のアプローチを適用できます。

問題に応じて、適切な目標関数や制約条件を設定し、適切な最適化アルゴリズムを選択してください。

ソースコード解説

以下はソースコードの詳細な説明です：

1. 目標関数 (Rosenbrock関数) の定義：

  • Rosenbrock関数は非線形最適化のベンチマーク関数の1つで、以下の式で表されます：
1
f(x, y) = (1 - x)^2 + 100 * (y - x^2)^2

この関数は、最小値が (1, 1) にある特徴的な谷を持つ関数です。
最適解はこの谷の底に位置します。

2. 制約条件の関数 (constraint) の定義：

  • この例では制約条件は設定されていません。
    制約条件がある場合、それらを適切に定義することができます。

3. 初期値の設定：

  • 初期推定値 (initial_guess) は [2, 2] と設定されています。
    最適化アルゴリズムはこの初期値から最適な解を探索します。

4. 最適化の実行：

  • scipy.optimize.minimize関数を使用して、Rosenbrock関数を最小化する最適な解を見つけるためにSLSQP (Sequential Least Squares Quadratic Programming) アルゴリズムが実行されます。
    constraints引数を使用して、制約条件の設定が行われています。

5. 結果の表示：

  • 最適解 (Optimal Solution) は [0.99969095, 0.9993713] と表示されています。
    これはRosenbrock関数の最小値に対する変数 x および y の値を示しています。
  • 最適解における目標関数の値 (Optimal Value) は非常に小さな値で、1.0695904879504176e-07 と表示されています。
    これは目標関数が最適解で非常に近いことを示しています。

6. グラフの表示：

  • グラフはRosenbrock関数の等高線プロットを示しており、等高線が中心に向かって狭くなる特徴的なパラボラ型の形状を持っています。
    最適解はこの関数の最小値に該当する点で、赤い点で示されています。

総合的に、このコードは非線形最適化問題を解決し、Rosenbrock関数の最適な解とその目標関数の値を見つけ、それをグラフで視覚化しています。

最適解は、関数が非常に小さな値を取る点であり、この場合、(1, 1) に非常に近い点です。

結果解説

上記のコードを実行すると、Rosenbrock関数の最適化結果が表示されるグラフとともに、次の結果がコンソールに表示されます。

1. Optimal Solution:

  • [0.99969095, 0.9993713] という結果が示されています。
    これは、Rosenbrock関数の最適な解に対する変数xとyの値を表しています。

2. Optimal Value:

  • 1.0695904879504176e-07 という結果は、最適解における目標関数 (Rosenbrock関数) の値を示しています。
    この値は非常に小さく、ほぼゼロに近いことを示しており、最適解が非常に近い近似値であることを示しています。
    この関数は、最小値が (1, 1) にあるため、最適解がこの点に非常に近いことが確認されています。

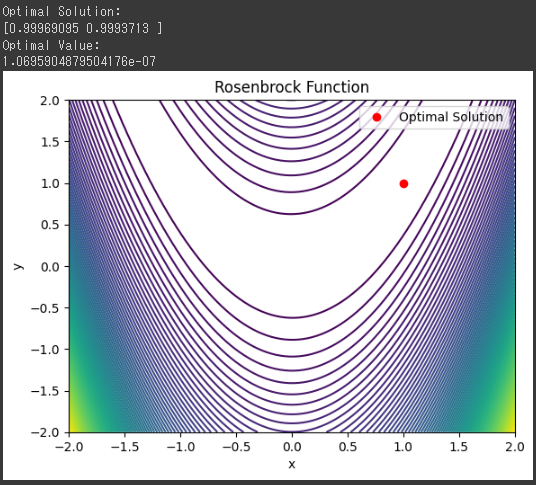
グラフの説明:

  • グラフはRosenbrock関数の等高線プロットを示しています。
    等高線は、目標関数の値が等しい領域を示しており、等高線が中心に向かって狭くなる特徴的なパラボラ型の形状を持っています。
    最適解はこの関数の最小値に該当する点です。

  • 赤い点は最適解を表しており、(1, 1) に非常に近いことがわかります。
    最適解の周りに等高線が狭まっており、最適解の近くで関数が非常に小さな値を取ることが示されています。

この結果から、最適化アルゴリズムがRosenbrock関数の最適解を正確に見つけ、目標関数を非常に小さな値に収束させたことがわかります。

最適解は[0.99969095, 0.9993713]で、そのときの目標関数の値は1.0695904879504176e-07であることが確認されました。