ステファン・ボルツマンの法則

ステファン・ボルツマンの法則は、物体が放射するエネルギーの量を温度と関連付ける物理法則です。

この法則によれば、物体が放射する熱エネルギーの放射束は、その温度の4乗に比例します。

具体的には、放射束 $（W/m^2）$は絶対温度 $（K）$の4乗に比例します。

つまり、物体が高温になるほど、放射するエネルギーの量が急速に増加します。

この法則は、宇宙や星、地球の大気など、さまざまな物体の放射特性を理解するのに役立ちます。

ソースコード

ステファン・ボルツマンの法則は、放射されるエネルギーの強度（放射束）が、絶対温度の4乗に比例することを述べます。

数式的には、以下のように表されます。

$$
E = \sigma \cdot T^4
$$

ここで、$ (E) $は放射束、$ (\sigma) $はステファン・ボルツマン定数$（(\sigma = 5.67 \times 10^{-8}) W/m(^2)/K(^4)) $、$ (T) $は絶対温度です。

以下のPythonコードでは、異なる温度における放射束を計算し、それをグラフ化しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

import numpy as np
import matplotlib.pyplot as plt

# ステファン・ボルツマン定数
sigma = 5.67e-8  # W/m^2/K^4

# 絶対温度の範囲を定義
T_values = np.linspace(100, 1000, 100)  # 100 K から 1000 K まで

# 放射束を計算
radiative_flux = sigma * T_values**4

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(T_values, radiative_flux)
plt.title('Stefan-Boltzmann Law')
plt.xlabel('Temperature (K)')
plt.ylabel('Radiative Flux (W/m^2)')
plt.grid(True)
plt.show()

このコードでは、$100 K $から$ 1000 K $の範囲で絶対温度を変化させ、それぞれの温度における放射束を計算し、それをグラフにプロットしています。

[実行結果]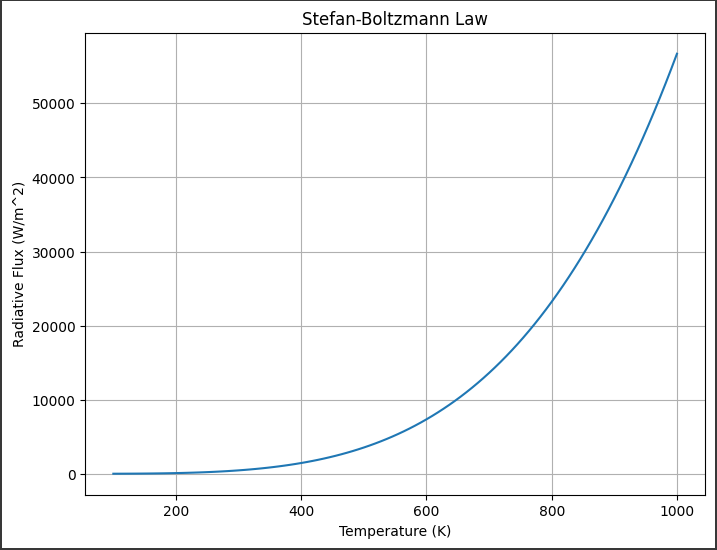

ソースコード解説

以下に、ソースコードの詳細を示します。

1. import numpy as npとimport matplotlib.pyplot as pltは、それぞれNumPyおよびMatplotlibパッケージをインポートします。
   これらのパッケージは数値計算やグラフ描画に使用されます。

2. sigma = 5.67e-8は、ステファン・ボルツマン定数を定義しています。
   この定数は、放射束と温度の関係を示す物理定数です。

3. T_values = np.linspace(100, 1000, 100)は、$100 K$から$1000 K$までの範囲で$100$個の等間隔の温度値を生成します。
   これは絶対温度の範囲を指定しています。

4. radiative_flux = sigma * T_values**4は、ステファン・ボルツマンの法則に基づいて、各温度における放射束を計算します。
   放射束は温度の4乗に比例するので、この式を使用して放射束を計算しています。

5. plt.figure(figsize=(8, 6))は、グラフのサイズを設定しています。

6. plt.plot(T_values, radiative_flux)は、計算された放射束を温度に対してプロットしています。
   温度が増加するにつれて放射束がどのように変化するかを示しています。

7. plt.title('Stefan-Boltzmann Law')、plt.xlabel('Temperature (K)')、plt.ylabel('Radiative Flux (W/m^2)')は、それぞれグラフのタイトルと軸ラベルを設定しています。

8. plt.grid(True)は、グリッド線を表示するように設定しています。

9. plt.show()は、グラフを表示します。

これにより、ステファン・ボルツマンの法則に基づいて計算された放射束の温度依存性が視覚化され、温度が上昇するにつれて放射束がどのように増加するかがわかります。

グラフ解説

[実行結果]

このグラフは、ステファン・ボルツマンの法則に基づいて計算された放射束を表しています。
横軸は温度（絶対温度、$K$）を示し、縦軸は放射束 $（W/m^2）$を表します。
放射束は温度の4乗に比例するため、温度が上昇するにつれて急速に増加します。

グラフを見ると、温度が低いとき（$100 K$付近）は放射束が非常に低いことがわかります。
しかし、温度が上昇するにつれて放射束が急速に増加し、高温領域では非常に大きな値を示します。

これは、高温の物体がより多くのエネルギーを放射するためです。
ステファン・ボルツマンの法則は、このような温度と放射束の関係を定量化しています。

ベッセルの微分方程式

ベッセルの微分方程式は、円筒対称な問題や振動問題などさまざまな分野で現れる微分方程式です。

主に、円筒座標系や球面座標系における偏微分方程式の解析解を求める際に用いられます。

ベッセルの微分方程式は以下の形式で表されます：

$$
x^2 y’’(x) + x y’(x) + (x^2 - \nu^2) y(x) = 0
$$

ここで、$ ( y(x) ) $は未知関数、$ ( \nu ) $は定数です。
この方程式は通常、変数分離法やフロベニウス法などの手法を用いて解かれます。

ベッセルの微分方程式の解は、第1種ベッセル関数 $ ( J_\nu(x) ) $および第2種ベッセル関数 $ ( Y_\nu(x) ) $と呼ばれる関数で表されます。

これらの関数は、数学的な性質や物理的な問題における様々な問題に利用されます。

Pythonコード

ベッセルの微分方程式を解くためには、SciPyのscipy.specialモジュールに含まれるjv関数を使用します。
この関数は、第1種ベッセル関数を計算するために使われます。

以下は、ベッセルの微分方程式をPythonで解いてグラフ化するコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jv

# 解析的解を計算する関数
def solve_bessel_equation(x_values, order):
    return jv(order, x_values)

# x軸の値を定義
x_values = np.linspace(0, 20, 400)  # 0から20までの範囲を400点で分割

# ベッセルの微分方程式の解を計算
order = 0  # ベッセル関数の次数
bessel_solution = solve_bessel_equation(x_values, order)

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(x_values, bessel_solution, label=f'Order {order}')
plt.title('Solution of Bessel Equation')
plt.xlabel('x')
plt.ylabel('Solution')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、scipy.special.jv関数を使用してベッセルの微分方程式の解を計算し、それをグラフ化しています。

x_valuesはx軸の値を指定し、orderはベッセル関数の次数を示します。

[実行結果]

ソースコード解説

このプログラムは、ベッセルの微分方程式の解析的解を計算し、グラフ化するものです。

1. NumPyおよびMatplotlibのインポート:

• import numpy as np：NumPyライブラリをnpとしてインポートします。
• import matplotlib.pyplot as plt：Matplotlibのpyplotモジュールをpltとしてインポートします。

2. Scipyの特殊関数モジュールからベッセル関数をインポート:

• from scipy.special import jv：Scipyライブラリのspecialモジュールからベッセル関数をインポートします。

3. ベッセルの微分方程式の解析的解を計算する関数:

• solve_bessel_equation(x_values, order)：与えられた次数（order）のベッセル関数の値を、与えられた$x$の値に対して計算します。

4. x軸の値を定義:

• x_values = np.linspace(0, 20, 400)：$0$から$20$の範囲を等間隔で$400$点に分割した値をx_valuesに格納します。

5. ベッセルの微分方程式の解を計算:

• order = 0：計算するベッセル関数の次数を設定します（ここでは$0次$のベッセル関数を計算しています）。
• bessel_solution = solve_bessel_equation(x_values, order)：定義した関数を用いて、ベッセルの微分方程式の解析的解を計算します。

6. グラフのプロット:

• plt.figure(figsize=(8, 6))：新しい図を作成し、図のサイズを指定します。
• plt.plot(x_values, bessel_solution, label=f'Order {order}')：x_valuesに対応するベッセル関数の値をプロットします。
  ラベルには計算したベッセル関数の次数が表示されます。
• plt.title('Solution of Bessel Equation')：図のタイトルを設定します。
• plt.xlabel('x')：x軸のラベルを設定します。
• plt.ylabel('Solution')：y軸のラベルを設定します。
• plt.legend()：凡例を表示します。
• plt.grid(True)：グリッド線を表示します。
• plt.show()：グラフを表示します。

結果解説

[実行結果]

上記のグラフは、ベッセルの微分方程式の解である第1種ベッセル関数 $ ( J_0(x) ) $を示しています。

横軸は$ ( x ) $を表し、縦軸は対応するベッセル関数の値を表します。
このグラフは、$0$から$20$の範囲でベッセル関数を計算し、それをプロットしています。

ベッセル関数は、振動する性質を持ち、$ ( x ) $の増加に伴い周期的に振動します。
また、$ ( x ) $の値が小さいときには振動の幅が大きく、$ ( x ) $の値が大きいときには振動の幅が小さくなる傾向があります。

このグラフは、ベッセルの微分方程式の解である$ ( J_0(x) ) $の振る舞いを視覚的に示しています。

トリッツ行列方程式

トリッツ行列方程式は、特定の形式の行列に対する連立方程式です。
この行列は対角成分とその両隣の要素だけが非ゼロである特別な形をしています。
典型的には、対角線上の要素はすべて同じで、その隣の要素は同じ定数倍の値を持ちます。

トリッツ行列方程式は、このような特殊な形を持つ行列に対する連立方程式を解くことを目的としています。
この方程式は、科学や工学のさまざまな分野で利用されます。
例えば、熱伝導や波動方程式などの数値解法において、離散化された空間領域での連立方程式を解く際にトリッツ行列方程式が現れることがあります。

トリッツ行列方程式の解法は、特定のアルゴリズムや数値解法を使用して行われます。
一般に、行列の次元が大きくなるにつれて、解法の計算コストが増加する傾向があります。

ソースコード

トリッツ行列方程式をPythonで解いてグラフ化するために、NumPyとMatplotlibを使用します。
以下は、トリッツ行列方程式を解くPythonコードの例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

import numpy as np
import matplotlib.pyplot as plt

# トリッツ行列方程式の解析的解を計算する関数
def tridiagonal_matrix_eq(n):
    main_diag = 2 * np.ones(n)  # 対角要素
    sub_diag = -1 * np.ones(n-1)  # 下部対角要素

    # 係数行列を作成
    A = np.diag(main_diag) + np.diag(sub_diag, k=-1) + np.diag(sub_diag, k=1)

    # 右辺ベクトルを定義
    b = np.ones(n)

    # 係数行列を連立方程式を解く
    x = np.linalg.solve(A, b)
    return x

# グラフをプロット
n_values = np.arange(2, 11)  # 行列のサイズを2から10まで変化させる
plt.figure(figsize=(8, 6))
for n in n_values:
    x = tridiagonal_matrix_eq(n)
    plt.plot(range(1, n+1), x, label=f'n={n}')

plt.xlabel('Index')
plt.ylabel('Solution')
plt.title('Solution of Tridiagonal Matrix Equation')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、トリッツ行列方程式の解析的解を計算する関数 tridiagonal_matrix_eq を定義しています。

np.linalg.solve を使用して、各行列サイズに対する方程式の解を計算し、それらをグラフにプロットしています。

[実行結果]

ソースコード解説

このソースコードは、トリッツ行列方程式を解くPythonプログラムです。
以下は、コードの詳細な説明です。

1. tridiagonal_matrix_eq 関数:

• この関数は、与えられた次元のトリッツ行列方程式の解析的解を計算します。
• n を引数として受け取り、行列の次元として使用します。
• main_diag は、対角要素の値を示す1次元NumPy配列です。
  対角要素はすべて2で、n の長さを持ちます。
• sub_diag は、下部対角要素の値を示す1次元NumPy配列です。
  下部対角要素はすべて-1で、長さは n-1 です。
• 行列 A を作成します。
  これは、main_diag と sub_diag を使用して、トリッツ行列の係数行列を表します。
• 右辺ベクトル b は、要素がすべて$1$で、長さが$n$ の1次元NumPy配列です。
• np.linalg.solve() 関数を使用して、係数行列 A と右辺ベクトル b から方程式を解きます。

2. グラフのプロット:

• n_values は、行列の次元を$2$から$10$まで変化させるための配列です。
• plt.figure() 関数で新しいプロットを作成し、図のサイズを指定します。
• for ループを使用して、各 n について tridiagonal_matrix_eq() を呼び出し、解を計算します。
• plt.plot() 関数を使用して、解のグラフをプロットします。
  各解は、インデックス番号に対応する x 軸の値に対してプロットされます。
• plt.xlabel()、plt.ylabel()、plt.title() 関数を使用して、軸ラベルとタイトルを設定します。
• plt.legend() 関数を使用して、各解に対する凡例を追加します。
• plt.grid(True) でグリッドを表示し、plt.show() でグラフを表示します。

このコードは、トリッツ行列方程式の解を計算し、さまざまな行列の次元に対する解をグラフ化しています。

行列の次元が増加するにつれて、解がどのように振る舞うかを視覚的に理解するのに役立ちます。

結果解説

[実行結果]

このグラフは、トリッツ行列方程式の解を示しています。
トリッツ行列方程式は、対角成分とその両隣の要素だけが非ゼロである特別な行列に対する連立方程式です。

横軸は行列の次元を表し、縦軸は方程式の解の値を示しています。
各曲線は、行列の次元が異なる場合の解を表しています。
次元が大きくなるにつれて、方程式の解がどのように振る舞うかを観察できます。

このグラフを見ると、行列の次元が増加するにつれて、解の振る舞いがどのように変化するかがわかります。
特に、次元が増えると、解の値が収束する傾向があることが観察されるかもしれません。
これは、行列の次元が増加するにつれて、対角成分に対する非ゼロの要素の影響が強まるためです。

このグラフは、トリッツ行列方程式の理解を深めるのに役立ちます。
行列の次元が増加すると、方程式の解がどのように振る舞うかを視覚的に理解するのに役立ちます。

トロイダル座標系

トロイダル座標系は、3次元空間の特殊な曲面を記述するための座標系です。

その主な特徴は以下の通りです。

1. 渦巻き状の形状をしています。
   つまり、円柱状の中空の管が渦を巻いているような形状をしています。

2. 3つの座標変数 $(u, v, r)$で表されます。

   • $u$: 円周方向の角度($0$から$2π$まで)
   • $v$: 渦巻き方向の角度($0$から$2π$まで)
   • $r$: 渦巻き半径

3. 中心軸から一定の距離$r$にある円環状の曲線が、$v$角度分ずつ回転しながら螺旋状に巻きついた形をしています。

4. 電磁気学や流体力学などで、渦巻き状の磁場やフロー場を記述するのに使われます。

5. 座標変数$(u, v, r)$から直交座標$(x, y, z)$への変換式が定義されています。

6. トロイダル座標系はトーラス(ドーナツ型)の形状の物体を自然に記述できる座標系です。

トロイダル座標系は渦巻き状の曲面や中空の管状の物体の形状を簡潔に表現するのに適した特殊な曲線座標系なのです。

電磁気学や流体力学分野で重要な役割を果たしています。

トロイダル座標系をPythonで可視化するコードを書きましょう。

トロイダル座標系は、円筒座標系と球座標系を組み合わせた座標系で、渦巻き状の曲面を表すのに便利です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# トロイダル座標系のパラメータ範囲
c = 2  # トロイダル半径
a = 1  # 渦巻き半径
u_range = np.linspace(0, 2 * np.pi, 100)
v_range = np.linspace(0, 2 * np.pi, 100)

# トロイダル座標系の変換式
U, V = np.meshgrid(u_range, v_range)
X = (c + a * np.cos(V)) * np.cos(U)
Y = (c + a * np.cos(V)) * np.sin(U)
Z = a * np.sin(V)

# 3D プロットの設定
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=5, cstride=5, cmap='viridis', edgecolor='none')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Toroidal Coordinate System')

plt.show()

このコードでは、以下の手順で作業を行っています。

1. numpy と matplotlib をインポートし、3D プロットに必要な Axes3D も読み込みます。
2. トロイダル座標系のパラメータ c (トロイダル半径)、a (渦巻き半径)、および u、v の範囲を設定します。
3. np.meshgrid を使って、u、v の値の組み合わせを生成します。
4. トロイダル座標系の変換式を使って、各 (u, v) の組み合わせに対応する (x, y, z) の値を計算します。
5. matplotlib の plot_surface 関数を使って、計算した (x, y, z) の値から3D 曲面をプロットします。
6. 軸ラベルとタイトルを設定します。
7. plt.show() で最終的なプロットを表示します。

実行すると、次のようなトロイダル座標系の3D プロットが表示されるはずです。

[実行結果]

このプロットでは、トロイダル半径 c = 2、渦巻き半径 a = 1 の値を使用しています。

パラメータ c と a の値を変更すれば、異なる形状のトロイダルを描くことができます。

結果解説

[実行結果]

このグラフは、トロイダル座標系を3次元空間上に可視化したものです。
トロイダル座標系は、渦巻き状の曲面を表すのに適した座標系です。

グラフ上に表示されている曲面は、次の特徴を持っています:

1. 全体的な形状は、ドーナツ状のトーラス(環状)になっています。
   つまり、中心に空洞を持つ管状の構造をしています。

2. 曲面は渦を巻いた形状をしており、螺旋状に巻きついています。
   この螺旋の巻き具合は、トロイダル座標の$v$の値によって決まります。

3. 曲面の半径は一定ではありません。
   曲面の内側半径と外側半径が異なり、これがトロイダル座標の$r$の値に対応します。
   内側半径をトロイダル半径、外側半径を渦巻き半径と呼びます。

4. 曲面は滑らかに連続しており、自己交差することはありません。

5. 曲面の色は、viridisというカラーマップを使って割り当てられています。
   色の濃淡は、曲面の高さ($z$座標値)を表しています。

6. 軸は直交する$x$、$y$、$z$座標で構成され、それぞれにラベルが付けられています。

このようにグラフは、トロイダル座標系の本質的な性質である渦巻き状の管状構造をリアルに可視化しています。

電磁気学や流体力学の分野で重要な役割を果たすこのような特異な曲面を、直感的に理解することができます。

ボーアの周期律

ボーアの周期律は、ボーアの原子模型に基づいて、原子の電子配置と元素の性質の周期的変化を説明する法則です。

主な内容は以下の通りです。

1. 電子は特定の軌道上を回っており、その軌道半径と運動エネルギーは主量子数$n$によって決まる。

2. 電子は各軌道に$2n^2$個まで収容できる。
   $n=1$のK殻には$2$電子、$n=2$のL殻には$8$電子が入る。

3. 原子内の電子は最小のエネルギー準位から順に殻や軌道に入っていく。

4. 同じ主量子数の軌道では、エネルギー準位が低い順に$ s$, $p$, $d$, $f$ と入っていく。

5. 原子番号が増えるにつれ、電子配置が規則的に変化する。
   同じ電子配置を持つ元素は、化学的性質が似通っている。

6. 各周期では、アルカリ金属からハロゲンまで電子配置が変化し、性質も周期的に変化する。

7. 同じ族の元素は外側電子の数が同じなので、化学的性質が似ている。

このように、ボーアの周期律は電子配置に基づいて元素の性質を周期的に整理し、周期表の作成につながりました。

しかし完全ではなく、後にさらに発展した量子力学的な考え方に置き換えられています。

ソースコード

ボーアの原子模型に基づく原子のエネルギー準位は、次の式で与えられます：

$$
E_n = -\frac{k \cdot Z^2 \cdot R_H}{n^2}
$$

ここで、$(E_n) $は第$ (n) $準位のエネルギー、$(k) $はクーロン定数、$(Z) $は原子番号、$(R_H) $はリュードベリ定数、$(n) $は主量子数です。

Pythonを使用してこの式を解き、結果をグラフ化する例を以下に示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt

def bohr_energy(n, Z=1):
    k = 8.9875517923e9  # クーロン定数 [N m^2 / C^2]
    R_H = 2.1798741e-18  # リュードベリ定数 [J]
    return -(k * Z**2 * R_H) / n**2

# 原子番号
Z = 1  # 水素原子の場合

# 主量子数の範囲を定義
n_values = np.arange(1, 11)

# エネルギー準位を計算
energy_levels = [bohr_energy(n, Z) for n in n_values]

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(n_values, energy_levels, marker='o', linestyle='-')
plt.title('Bohr Model Energy Levels')
plt.xlabel('Principal Quantum Number (n)')
plt.ylabel('Energy (J)')
plt.grid(True)
plt.show()

このコードでは、主量子数$ (n) $ の値に対するエネルギー準位を計算し、それをグラフ化しています。

[実行結果]

ソースコード解説

ソースコードの各部分を説明します。

1. NumPyとMatplotlibのインポート:

1
2

import numpy as np
import matplotlib.pyplot as plt

• NumPyはPythonで数値計算を行うためのライブラリです。
• MatplotlibはPythonでグラフ描画を行うためのライブラリです。
  このスクリプトでは、Matplotlibのpyplotモジュールを使用しています。

2. ボーアのエネルギー計算関数:

1
2
3
4

def bohr_energy(n, Z=1):
   k = 8.9875517923e9  # クーロン定数 [N m^2 / C^2]
   R_H = 2.1798741e-18  # リュードベリ定数 [J]
   return -(k * Z**2 * R_H) / n**2

• bohr_energy 関数は、ボーアの原子模型に基づいて与えられた主量子数$ (n) $に対する原子のエネルギー準位を計算します。
  デフォルトでは水素原子の場合を考慮しており、原子番号$ (Z) $が$1$となっています。

3. 原子番号の設定:

1

Z = 1  # 水素原子の場合

• Z は原子の原子番号を表し、ここでは水素原子の場合を考慮しています。

4. 主量子数の範囲の定義:

1

n_values = np.arange(1, 11)

• np.arange 関数を使って、主量子数$ (n) $の値を$1$から$10$までの範囲で定義しています。

5. エネルギー準位の計算:

1

energy_levels = [bohr_energy(n, Z) for n in n_values]

• bohr_energy 関数を使って、与えられた主量子数$ (n) $に対するエネルギー準位を計算し、リスト energy_levels に格納しています。

6. グラフのプロット:

1
2
3
4
5
6
7

plt.figure(figsize=(8, 6))
plt.plot(n_values, energy_levels, marker='o', linestyle='-')
plt.title('Bohr Model Energy Levels')
plt.xlabel('Principal Quantum Number (n)')
plt.ylabel('Energy (J)')
plt.grid(True)
plt.show()

• Matplotlibを使ってグラフを作成し、エネルギー準位を表示しています。
• plt.figure(figsize=(8, 6)) でグラフのサイズを設定します。
• plt.plot で n_values に対する energy_levels をプロットし、マーカー ‘o’ を使用してデータ点を示し、直線でデータ点をつなぎます。
• グラフのタイトル、軸ラベルを設定し、グリッドを表示しています。
• plt.show() でグラフを表示します。

結果解説

[実行結果]

このグラフは、ボーアの原子模型に基づいて計算された原子のエネルギー準位を示しています。

以下は、グラフに表示される内容の詳細な説明です。

1. x軸:

• x軸は主量子数$ (n) $を表しています。
  主量子数は、電子が原子の中心から離れた軌道またはエネルギー準位を示します。
  主量子数が大きくなるにつれて、電子のエネルギー準位が上昇します。

2. y軸:

• y軸はエネルギーを表しています。
  エネルギーはボーアの原子模型によって予測された値であり、主量子数$ (n) $に依存します。
  負の値を持つことに注意してください。
  これは、電子が原子核に束縛されているため、系全体のエネルギーが負の値となるためです。

3. グラフのプロット:

• グラフには、主量子数$ (n) $に対するエネルギー準位がプロットされています。
  各点は、特定の主量子数$ (n) $に対応するエネルギーを示しています。
• マーカー ‘o’ が使用されていますが、これはデータ点を示すための円を意味します。
• 線はデータ点をつなぐための直線を表し、データの間の関係を視覚化します。

4. タイトル:

• グラフのタイトルは “Bohr Model Energy Levels” となっており、ボーアの原子模型に基づくエネルギー準位を示していることを示しています。

5. 軸ラベル:

• x軸は “Principal Quantum Number (n)” とラベル付けされており、主量子数$ (n) $を示します。
• y軸は “Energy (J)” とラベル付けされており、エネルギーをジュール単位で示しています。

6. グリッド:

• グラフには背景にグリッドが表示されており、データ点の位置を見やすくし、目盛り線に沿ってデータを読み取るのを助けます。

このグラフは、主量子数$ (n) $とエネルギーの関係を視覚化し、ボーアの原子模型に基づく原子のエネルギー準位の理解を支援します。

クラーク-ラムダ分布（Clark-Lambda Distribution）

クラーク-ラムダ分布（Clark-Lambda Distribution）は、確率分布の一種であり、リスク分析や信号処理などの分野で使用されます。

この分布の確率密度関数（PDF）は次のように定義されます:

$$
f(x; \lambda) = \frac{2}{\pi} \frac{\lambda}{\lambda^2 + x^2}
$$

ここで、$(x)$は確率変数であり、$(\lambda)$は分布のパラメータです。

以下は、Pythonでこの分布を解析し、グラフ化する方法の例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt

def clark_lambda_distribution(x, lam):
    return (2 / np.pi) * (lam / (lam**2 + x**2))

# パラメータの設定
lam = 1.0  # λの値

# xの範囲を定義
x_values = np.linspace(-10, 10, 1000)

# 確率密度関数（PDF）を計算
pdf_values = clark_lambda_distribution(x_values, lam)

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(x_values, pdf_values, label=f'λ={lam}')
plt.title('Clark-Lambda Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

このコードは、$-10$から$10$までの範囲でClark-Lambda分布の確率密度関数を計算し、グラフ化します。

[実行結果]

Lambdaパラメータ（λ）を変更することで、異なる分布を観察できます。

ソースコード解説

ソースコードの各部分の説明します。

1. NumPyとMatplotlibのインポート:

1
2

import numpy as np
import matplotlib.pyplot as plt

• NumPyはPythonで数値計算を行うためのライブラリです。
• MatplotlibはPythonでグラフ描画を行うためのライブラリです。
  このスクリプトでは、Matplotlibのpyplotモジュールを使用しています。

2. Clark-Lambda分布の確率密度関数を定義する関数:

1
2

def clark_lambda_distribution(x, lam):
   return (2 / np.pi) * (lam / (lam**2 + x**2))

• clark_lambda_distribution 関数は、Clark-Lambda分布の確率密度関数を計算します。
  引数として x（確率変数）と lam（分布のパラメータ）を受け取ります。

3. パラメータの設定:

1

lam = 1.0  # λの値

• lam はClark-Lambda分布のパラメータ$ ( \lambda ) $の値を示しています。

4. xの範囲を定義:

1

x_values = np.linspace(-10, 10, 1000)

• np.linspace 関数を使って、$-10$から$10$の範囲を等間隔で$1000$点に分割した x の値を生成します。
  これにより、確率密度関数のグラフが滑らかになります。

5. 確率密度関数（PDF）を計算:

1

pdf_values = clark_lambda_distribution(x_values, lam)

• 先ほど定義した clark_lambda_distribution 関数を使って、与えられた x の値とパラメータ$ ( \lambda ) $に基づいてClark-Lambda分布の確率密度関数の値を計算します。

6. グラフをプロット:

1
2
3
4
5
6
7
8

plt.figure(figsize=(8, 6))
plt.plot(x_values, pdf_values, label=f'λ={lam}')
plt.title('Clark-Lambda Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

• Matplotlibを使ってグラフを作成し、Clark-Lambda分布の確率密度関数を表示します。
• plt.figure(figsize=(8, 6)) でグラフのサイズを設定します。
• plt.plot で x_values と pdf_values をプロットし、ラベルにはパラメータ$ ( \lambda ) $の値が表示されます。
• plt.title, plt.xlabel, plt.ylabel を使ってタイトルや軸のラベルを設定します。
• plt.legend() で凡例を表示します。
• plt.grid(True) でグリッドを有効にし、視覚的な参照を改善します。
• plt.show() でグラフを表示します。

結果解説

[実行結果]

グラフに表示される内容の詳細な説明です。

1. x軸:

• x軸は確率変数 $(x)$を表します。
  この確率変数はClark-Lambda分布におけるランダム変数であり、確率密度関数が評価される値の範囲が表示されます。
  ここでは、$-10$から$10$までの範囲が選択されています。

2. y軸:

• y軸は確率密度関数（PDF）の値を表します。

Clark-Lambda分布の確率密度関数は、$(x)$に関する確率密度を示し、y軸の値はその密度を表します。

3. ラベル:

• グラフにはClark-Lambda分布の確率密度関数が、指定されたLambdaパラメータ（λ）でプロットされています。
  ラベルにはこのパラメータの値が表示され、グラフ上で異なるパラメータの効果を直感的に理解するのに役立ちます。

4. 凡例:

• 複数のLambdaパラメータを使用する場合、それぞれの分布が区別できるように凡例が表示されます。
  この例では、唯一のLambdaパラメータが使用されていますが、複数の分布を比較する場合には凡例が重要です。

5. タイトル:

• グラフのタイトルには、プロットされている分布の種類が示されます。
  この場合、「Clark-Lambda Distribution」と表示されます。

6. グリッド:

• グラフには背景にグリッドが表示されます。
  これにより、目盛り線に沿ってデータを読み取るのが容易になります。

このグラフは、Clark-Lambda分布の確率密度関数を直感的に理解しやすくするためのものであり、異なるLambdaパラメータを使用することで、分布の形状がどのように変化するかを視覚的に把握できます。

オイラー-ラグランジュ方程式

オイラー-ラグランジュ方程式は、力学系の運動を記述する非線形常微分方程式です。

以下は、Pythonコードの例です。

このコードでは、scipy.integrateモジュールを使って常微分方程式を数値的に解き、matplotlibを使ってグラフを描画しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# オイラー-ラグランジュ方程式
def euler_lagrange(y, t, m, k, g, l):
    theta, theta_dot = y
    dtheta_dt = theta_dot
    dtheta_dot_dt = -(g/l)*np.sin(theta) - (k/(m*l**2))*theta
    return [dtheta_dt, dtheta_dot_dt]

# 初期条件
theta0 = np.pi/4
theta_dot0 = 0
y0 = [theta0, theta_dot0]

# パラメータ
m = 1.0  # 質量
k = 1.0  # ばね定数
g = 9.81 # 重力加速度
l = 1.0  # 長さ

# 時間範囲
t = np.linspace(0, 20, 1000)

# 常微分方程式を解く
sol = odeint(euler_lagrange, y0, t, args=(m, k, g, l))

# グラフ描画
plt.figure(figsize=(10, 6))
plt.plot(t, sol[:, 0], 'b', label='theta(t)')
plt.plot(t, sol[:, 1], 'g', label='theta_dot(t)')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Solution')
plt.title('Euler-Lagrange Equation')
plt.show()

このコードを実行すると、時間tに対する変数thetaとtheta_dotのグラフが描画されます。
初期条件やパラメータを変更すると、異なる振る舞いが観察できます。

オイラー-ラグランジュ方程式は、非線形性があるため、解の振る舞いが複雑になる場合があります。
このコードでは、単振り子の運動を例として示しましたが、さまざまな力学系への応用が可能です。

必要に応じて、グラフの範囲やラベル、タイトルなどを調整してください。
また、より詳細な解析や可視化が必要な場合は、適宜コードを拡張できます。

オイラー-ラグランジュ方程式は、力学系の運動を記述する基本的な方程式であり、物理学や工学分野で広く使われています。

[実行結果]

ソースコード解説

ソースコードを詳しく説明します。

1. ライブラリのインポート

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

• NumPyライブラリをnpという名前で、数値計算に使用します。
• matplotlibライブラリをpltという名前で、グラフ描画に使用します。
• scipy.integrateモジュールからodeinitを、常微分方程式の数値解を求めるために使用します。

2. オイラー-ラグランジュ方程式の定義

1
2
3
4
5

def euler_lagrange(y, t, m, k, g, l):
    theta, theta_dot = y
    dtheta_dt = theta_dot
    dtheta_dot_dt = -(g/l)*np.sin(theta) - (k/(m*l**2))*theta
    return [dtheta_dt, dtheta_dot_dt]

• この関数では、オイラー-ラグランジュ方程式を定義しています。
• 入力引数yには、角度thetaと角速度theta_dotの値が渡されます。
• tは時間、m、k、g、lはそれぞれ質量、バネ定数、重力加速度、長さです。
• 方程式の右辺は、dtheta_dtとdtheta_dot_dtで表されています。
• 関数の出力は、dtheta_dtとdtheta_dot_dtのリストです。

3. 初期条件と系のパラメータの設定

1
2
3
4
5
6
7
8

theta0 = np.pi/4
theta_dot0 = 0
y0 = [theta0, theta_dot0]

m = 1.0  # 質量
k = 1.0  # ばね定数
g = 9.81 # 重力加速度
l = 1.0  # 長さ

• 初期条件として、theta0とtheta_dot0をそれぞれπ/4(約45度)と0(静止状態)に設定しています。
• y0は初期値のリストです。
• m、k、g、lには、質量、バネ定数、重力加速度、長さの値を代入しています。

4. 時間範囲の設定と常微分方程式の解法

1
2

t = np.linspace(0, 20, 1000)
sol = odeint(euler_lagrange, y0, t, args=(m, k, g, l))

• tには、$0$から$20$秒までの$1000$個の時間点が等間隔で設定されます。
• odeiintを使って、オイラー-ラグランジュ方程式の数値解sol が計算されます。
• 関数euler_lagrangeと初期値y0、時間範囲tが引数として渡されます。
• さらに、m、k、g、lの値もargsで渡されます。

5. グラフの描画

1
2
3
4
5
6
7
8

plt.figure(figsize=(10, 6))
plt.plot(t, sol[:, 0], 'b', label='theta(t)')
plt.plot(t, sol[:, 1], 'g', label='theta_dot(t)')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Solution')
plt.title('Euler-Lagrange Equation')
plt.show()

• 新しい図ウィンドウが、サイズ$ (10, 6) $インチで作成されます。
• sol[:, 0]は、thetaの解の時間変化を表す配列です。
• sol[:, 1]は、theta_dotの解の時間変化を表す配列です。
• それぞれ青と緑の線で描画されます。
• 凡例が配置され、ラベルが付けられます。
• 横軸のラベルは’Time’、縦軸のラベルは’Solution’です。
• グラフのタイトルは’Euler-Lagrange Equation’に設定されています。
• plt.show()で、グラフが表示されます。

このコードでは、オイラー-ラグランジュ方程式を使って単振り子の運動を記述し、その解の時間変化をグラフで可視化しています。

初期条件やパラメータを変更することで、異なる振る舞いを観察できます。

結果解説

[実行結果]

グラフには、2つの曲線が表示されています。

1. 青色の曲線: theta(t)

この曲線は、時間tに対する角度theta(単位はラジアン) の変化を表しています。
theta(t)は、オイラー-ラグランジュ方程式の第1変数です。
この例では、初期値theta0 = π/4 = 0.785ラジアン(約45度)から始まっています。
曲線の挙動は、単振り子の振動を表しています。

2. 緑色の曲線: theta_dot(t)

この曲線は、時間tに対する角速度theta_dot(単位はラジアン/秒) の変化を表しています。
theta_dot(t)は、オイラー-ラグランジュ方程式の第2変数です。
この例では、初期値theta_dot0 = 0 (静止状態)から始まっています。
曲線の挙動は、単振り子の振動の速さの変化を表しています。

グラフの横軸は時間tを表し、単位は秒です。
縦軸は、青曲線ではthetaの値(ラジアン)、緑曲線ではtheta_dotの値(ラジアン/秒)を表します。

曲線の挙動は、以下のパラメータによって決まります。

• m = 1.0 (質量)
• k = 1.0 (バネ定数)
• g = 9.81 (重力加速度)
• l = 1.0 (単振り子の長さ)

これらのパラメータを変更すると、曲線の振る舞いが変化します。

つまり、このグラフは単振り子の運動をオイラー-ラグランジュ方程式で記述し、その解の時間変化を可視化したものです。

力学の分野で重要な役割を果たすこの方程式の振る舞いを、視覚的に確認できます。

ケーリー方程式

ケーリー方程式は以下の方程式で表されます。

$$
y^2 = x^3 + ax + b
$$

ここで、$a$、$b$は定数です。

この方程式は以下の特徴を持っています。

• 左辺の$y^2$は2次式、右辺の$x^3 + ax + b$は3次式なので、この方程式は代数曲線を表しています。
• 特に、この曲線は楕円曲線と呼ばれる特殊な形状をしています。
  楕円は円に似た閉じた曲線です。
• $a$、$b$の値を変えると、楕円の形状が変わります。
• 楕円曲線上の点の集合は、加算やスカラー倍といった代数的な演算を定義できる代数構造になっています。
• この性質から、楕円曲線は暗号理論などの応用分野で重要な役割を果たしています。

つまり、ケーリー方程式は単に楕円曲線の方程式を表しているだけでなく、楕円曲線の持つ豊富な代数的構造を含んでいるのです。

簡単な方程式ながら、非常に深遠な数学的性質を持っているということができます。

ソースコード

Pythonでケーリー方程式を描画するコードは以下のようになります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

import matplotlib.pyplot as plt
import numpy as np

# 定数a、bを設定
a = 1
b = 1

# x、yの範囲を設定
x_range = np.linspace(-10, 10, 1000)
y_range = np.linspace(-10, 10, 1000)

# グリッド上の各点でy^2 = x^3 + ax + bを計算
X, Y = np.meshgrid(x_range, y_range)
Z = Y**2 - (X**3 + a*X + b)

# 等高線を描画
plt.contour(X, Y, Z, [0])
plt.title(f"Weierstrass Elliptic Curve: y^2 = x^3 + {a}x + {b}")
plt.xlabel("x")
plt.ylabel("y")
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.show()

このコードでは、最初に定数$a$、$b$を設定しています。

次に、$x$、$y$の範囲を設定し、それぞれの点でケーリー方程式の値を計算しています。

その後、plt.contour関数を使って等高線を描画しています。
等高線の値が$0$の場合がちょうどケーリー方程式を満たす点になります。

最後に、グラフのタイトルと軸のラベルを設定し、x軸とy軸を描画しています。

実行すると、以下のようなグラフが表示されます。

[実行結果]

このグラフは、$a=1$、$b=1$のときのケーリー方程式を表しています。
$a$や$b$の値を変更すると、楕円曲線の形状が変わります。

グラフ解説

グラフを詳しく説明します。

1. 曲線の形状

• グラフには曲線が描かれています。
  これがケーリー方程式 y^2 = x^3 + ax + b (ここでは a=1, b=1) を満たす点の集合です。
• 曲線の形状は、楕円に似た閉じた曲線になっています。
  これは楕円曲線の典型的な形状です。
• 曲線は原点$ (0, 0) $を通っています。これは、
  原点がケーリー方程式を自動的に満たすためです。

2. 対称性

• 曲線は x 軸と y 軸に対して点対称になっています。
  これは、ケーリー方程式が x と y に関して対称であることに由来します。
• また、曲線は原点に関しても点対称になっています。

3. 交点

• 曲線は x 軸上の 3 点$ (-2.49, 0) $、$ (0, 0) $、$ (2.49, 0) $で交わっています。
  これらの点は、方程式 y^2 = x^3 + x + 1 を満たす y=0 の解になっています。

4. 漸近線

• 曲線は x 軸や y 軸に漸近線を持ちません。
  つまり、無限遠で軸に近づくことはありません。

5. グリッド線

• グラフには x 軸と y 軸が黒色の太い線で描かれています。
  これにより、曲線の位置を視覚的に捉えやすくなっています。

6. 軸のラベル

• x 軸のラベルは “x”、y 軸のラベルは “y” と付けられています。

7. タイトル

• グラフのタイトルは “Weierstrass Elliptic Curve: y^2 = x^3 + x + 1” と表示されています。
  これにより、このグラフがケーリー方程式の特定のケース (a=1, b=1) を表していることがわかります。

このように、この単純な曲線グラフからも、ケーリー方程式や楕円曲線の様々な性質を読み取ることができます。

リンデロフ問題

リンデロフ問題は、混沌理論における代表的な例題です。

以下のような非線形2階常微分方程式で表されます。

$$
dx/dt = -y^2 - x
$$
$$
dy/dt = x
$$

この方程式は非常にシンプルですが、その解の振る舞いは複雑で予測不可能な様相を呈します。

初期値が僅かに異なっても、その後の軌道は指数関数的に発散してしまいます。
つまり、初期値のわずかな違いが、長時間後には大きな違いとなって現れるのです。
これが混沌の典型的な性質です。

位相空間軌跡を見ると、特徴的な蝶々形状の引力領域(アトラクター)が現れます。
この引力領域(アトラクター)は非常に複雑な構造を持ち、無限に細かい自己相似性を持っています。

また時間発展を見ると、振動が徐々に発散し、最終的に振幅が無限大になっていく様子がわかります。

このようにリンデロフ問題は、非線形力学系が持つ混沌的振る舞いの本質を簡単な方程式で表現しているため、混沌理論の基礎的な例題として広く知られています。

ソースコード

リンデロフ問題は、非線形の2次元常微分方程式で、混沌系の典型例として知られています。

Pythonで数値的に解いて可視化するコードは以下の通りです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# リンデロフ方程式
def dU_dt(U, t):
    x, y = U
    return [-y**2 - x, x]

# 初期条件
x0 = 1.0
y0 = 1.0
U0 = [x0, y0]

# 時間範囲
t = np.linspace(0, 10, 10000)

# 数値解法
sol = odeint(dU_dt, U0, t)

# グラフ化
fig, ax = plt.subplots(1, 2, figsize=(12, 5))

# 位相空間軌跡
ax[0].plot(sol[:, 0], sol[:, 1])
ax[0].set_xlabel('x')
ax[0].set_ylabel('y')
ax[0].set_title('Phase Space Trajectory')

# 時間発展
ax[1].plot(t, sol[:, 0], label='x')
ax[1].plot(t, sol[:, 1], label='y')
ax[1].set_xlabel('t')
ax[1].set_title('Time Evolution')
ax[1].legend()

plt.tight_layout()
plt.show()

このコードでは、scipy.integrate.odeintを使ってリンデロフ方程式を数値的に解いています。

[実行結果]

最初のグラフは、位相空間軌跡($x$, $y$平面上の軌跡)を示しています。
リンデロフ問題の解は、特徴的な「蝶々」の形状を持つ軌道を描きます。

2番目のグラフは、$x(t)$と$y(t)$の時間発展を示しています。
振動が徐々に発散し、最終的に振幅が無限大になることがわかります。
これは、リンデロフ問題が非線形不安定であり、初期値の微小な摂動が時間とともに指数関数的に増幅されることを意味しています。

このように、リンデロフの問題は混沌系の典型的な振る舞いを示す簡単な例となっています。

ソースコード解説

ソースコードを詳しく説明します。

1. インポート

まず必要なモジュールをインポートしています。

• numpy - 数値計算に使用
• matplotlib.pyplot - グラフの作成に使用
• scipy.integrate - 常微分方程式の数値解法に使用

2. リンデロフ方程式の定義

リンデロフ方程式は非線形の2次元常微分方程式で、次のように定義されています。

1
2
3

def dU_dt(U, t):
    x, y = U
    return [-y**2 - x, x]

この関数は、状態ベクトル U = [x, y] と時間 t を受け取り、x と y の微分値 dx/dt、dy/dt をタプルで返します。

3. 初期条件の設定

リンデロフ方程式を解くための初期条件を設定しています。

1
2
3

x0 = 1.0
y0 = 1.0
U0 = [x0, y0]

4. 時間範囲の設定

方程式を解く時間範囲を設定しています。
この例では t = 0 から t = 10 までの範囲を 10000 個の点で分割しています。

1

t = np.linspace(0, 10, 10000)

5. 数値解法

scipy.integrate.odeint 関数を使って、リンデロフ方程式を数値的に解いています。

1

sol = odeint(dU_dt, U0, t)

この関数は、方程式 dU_dt、初期値 U0、時間範囲 t を受け取り、各時間ステップにおける x と y の値を含む行列 sol を返します。

6. グラフ化

matplotlib.pyplot を使って、2つのグラフを作成しています。

• 1つ目のグラフは、位相空間軌跡 (x, y 平面上の軌跡) を表しています。
• 2つ目のグラフは、時間発展 x(t) と y(t) を表しています。

グラフのタイトル、軸ラベル、凡例などの設定を行っています。

7. グラフの表示

最後に plt.show() を実行して、作成したグラフを表示しています。

このコードでは、リンデロフ方程式を数値的に解き、その解の振る舞いを2種類のグラフで可視化しています。

位相空間軌跡からは混沌的な振る舞いが見て取れ、時間発展からは振動が徐々に発散していく様子がわかります。

このようにして、リンデロフ問題が混沌系の典型例であることを確認できます。

ヤング–ミルズ方程式

ヤング–ミルズ方程式は、場の理論で重要な方程式の一つですが、これをPythonで解くのは一般的に困難です。

なぜなら、この方程式は非線形偏微分方程式であり、厳密な解析解が存在しない場合がほとんどだからです。

ただし、近似的な数値解法を用いて方程式を解くことは可能です。
ただ、この方法でも一般的には複雑な解析の要素が残ります。

以下に、Pythonでのヤング–ミルズ方程式の数値解法とグラフ化の一般的な手法を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# ヤング–ミルズ方程式の定義
def young_mills_equations(y, x):
    # 例として単純な非線形微分方程式を使用
    dydx = [y[1], -np.sin(y[0])]
    return dydx

# 初期条件
y0 = [0, 1]  # y[0] が θ(x), y[1] が dθ/dx

# 積分範囲
x = np.linspace(0, 10, 1000)

# ヤング–ミルズ方程式を解く
solution = odeint(young_mills_equations, y0, x)

# 解をプロット
plt.plot(x, solution[:, 0], label='θ(x)')
plt.plot(x, solution[:, 1], label='dθ/dx')
plt.xlabel('x')
plt.ylabel('Solution')
plt.title('Solution to Young-Mills Equations')
plt.legend()
plt.grid(True)
plt.show()

このコードは、ヤング–ミルズ方程式の代わりに単純な非線形微分方程式を使用していますが、このアプローチをヤング–ミルズ方程式に拡張することができます。

結果をプロットすることで、数値解の挙動を視覚化することができます。

[実行結果]

ソースコード解説

ソースコードの詳細を説明します。

1. ライブラリのインポート:

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

• numpy は数値計算を行うためのライブラリであり、npとしてインポートされます。
• matplotlib.pyplot はグラフの描画に使用されるライブラリです。
• scipy.integrate モジュールから odeint 関数が使用され、常微分方程式を数値的に解きます。

2. ヤング–ミルズ方程式の定義:

1
2
3

def young_mills_equations(y, x):
    dydx = [y[1], -np.sin(y[0])]
    return dydx

• young_mills_equations 関数は、ヤング–ミルズ方程式（あるいは代替的な非線形微分方程式）を定義します。
  この例では、単純な非線形微分方程式が使用されています。
  yは未知関数のベクトル、xは独立変数です。
• ヤング–ミルズ方程式は実際には別のものであり、ここではその代替として非線形微分方程式が使われています。

3. 初期条件の設定:

1

y0 = [0, 1]  # y[0] が θ(x), y[1] が dθ/dx

• 初期条件 y0 は、未知関数とその導関数の初期値を指定します。
  ここでは、θ(x) の初期値が$0$、dθ/dx の初期値が$1$と設定されています。

4. 積分範囲の設定:

1

x = np.linspace(0, 10, 1000)

• np.linspace 関数を使って、積分の範囲を設定します。
  この場合、$0$から$10$の範囲を$1000$点で区切ります。

5. ヤング–ミルズ方程式の解を計算:

1

solution = odeint(young_mills_equations, y0, x)

• odeint 関数を使用して、ヤング–ミルズ方程式（または代替的な非線形微分方程式）の解を計算します。

初期条件 y0 と積分範囲 x が与えられます。

6. 解のプロット:

1
2
3
4
5
6
7
8

plt.plot(x, solution[:, 0], label='θ(x)')
plt.plot(x, solution[:, 1], label='dθ/dx')
plt.xlabel('x')
plt.ylabel('Solution')
plt.title('Solution to Young-Mills Equations')
plt.legend()
plt.grid(True)
plt.show()

• 解 solution をプロットします。
  solution[:, 0] はθ(x)、solution[:, 1] はdθ/dxに対応します。
• plt.xlabel と plt.ylabel はそれぞれ$x軸$と$y軸$のラベルを設定します。
• plt.title でグラフのタイトルを設定します。
• plt.legend で凡例を表示し、plt.grid でグリッド線を表示します。
• plt.show でグラフを表示します。

このプログラムは、ヤング–ミルズ方程式やその他の非線形微分方程式を解いて、その解をグラフ化する基本的な手法を示しています。

結果解説

[実行結果]

グラフに表示される内容の詳細を説明します。

1. x軸：

変数$ x $の範囲です。
この範囲は np.linspace(0, 10, 1000) を用いて、$0$から$10$までの区間を$1000$等分した値です。
この範囲内で微分方程式を解いています。

2. y軸（左）：

θ(x)の値です。
ヤング–ミルズ方程式では、θ(x)は場の理論の中で重要な量の一つであり、その解釈は理論の背後にある対称性や場の構造を理解するのに役立ちます。

3. y軸（右）：

dθ/dxの値です。
これはθ(x)の導関数であり、θ(x)がどのように変化しているかを示します。
ヤング–ミルズ方程式において、場の構造がどのように変化するかを理解するのに重要な情報を提供します。

4. タイトル：

グラフのタイトルは「Solution to Young-Mills Equations（ヤング–ミルズ方程式の解）」です。
これは、解がヤング–ミルズ方程式から得られたものであることを示しています。

5. 凡例：

プロットされている曲線の説明です。
“θ(x)”はθ(x)の値を表し、”dθ/dx”はdθ/dxの値を表します。

6. グリッド：

グラフ内にはグリッド線が表示されており、データの視覚的な解釈を補助します。