トリッツ行列方程式

トリッツ行列方程式

トリッツ行列方程式は、特定の形式の行列に対する連立方程式です。
この行列は対角成分とその両隣の要素だけが非ゼロである特別な形をしています。
典型的には、対角線上の要素はすべて同じで、その隣の要素は同じ定数倍の値を持ちます。

トリッツ行列方程式は、このような特殊な形を持つ行列に対する連立方程式を解くことを目的としています。
この方程式は、科学や工学のさまざまな分野で利用されます。
例えば、熱伝導や波動方程式などの数値解法において、離散化された空間領域での連立方程式を解く際にトリッツ行列方程式が現れることがあります。

トリッツ行列方程式の解法は、特定のアルゴリズムや数値解法を使用して行われます。
一般に、行列の次元が大きくなるにつれて、解法の計算コストが増加する傾向があります。

ソースコード

トリッツ行列方程式をPythonで解いてグラフ化するために、NumPyとMatplotlibを使用します。
以下は、トリッツ行列方程式を解くPythonコードの例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
import numpy as np
import matplotlib.pyplot as plt

# トリッツ行列方程式の解析的解を計算する関数
def tridiagonal_matrix_eq(n):
    main_diag = 2 * np.ones(n)  # 対角要素
    sub_diag = -1 * np.ones(n-1)  # 下部対角要素

    # 係数行列を作成
    A = np.diag(main_diag) + np.diag(sub_diag, k=-1) + np.diag(sub_diag, k=1)

    # 右辺ベクトルを定義
    b = np.ones(n)

    # 係数行列を連立方程式を解く
    x = np.linalg.solve(A, b)
    return x

# グラフをプロット
n_values = np.arange(2, 11)  # 行列のサイズを2から10まで変化させる
plt.figure(figsize=(8, 6))
for n in n_values:
    x = tridiagonal_matrix_eq(n)
    plt.plot(range(1, n+1), x, label=f'n={n}')

plt.xlabel('Index')
plt.ylabel('Solution')
plt.title('Solution of Tridiagonal Matrix Equation')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、トリッツ行列方程式の解析的解を計算する関数 tridiagonal_matrix_eq を定義しています。

np.linalg.solve を使用して、各行列サイズに対する方程式の解を計算し、それらをグラフにプロットしています。

[実行結果]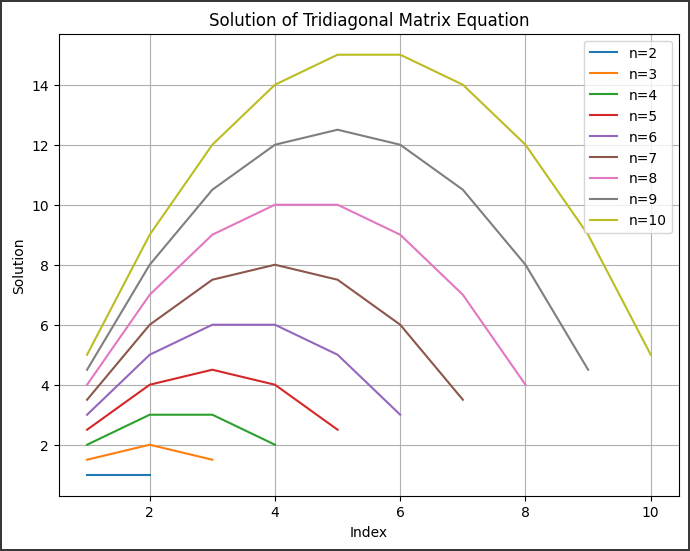

ソースコード解説

このソースコードは、トリッツ行列方程式を解くPythonプログラムです。
以下は、コードの詳細な説明です。

1. tridiagonal_matrix_eq 関数:

  • この関数は、与えられた次元のトリッツ行列方程式の解析的解を計算します。
  • n を引数として受け取り、行列の次元として使用します。
  • main_diag は、対角要素の値を示す1次元NumPy配列です。
    対角要素はすべて2で、n の長さを持ちます。
  • sub_diag は、下部対角要素の値を示す1次元NumPy配列です。
    下部対角要素はすべて-1で、長さは n-1 です。
  • 行列 A を作成します。
    これは、main_diag と sub_diag を使用して、トリッツ行列の係数行列を表します。
  • 右辺ベクトル b は、要素がすべて$1$で、長さが$n$ の1次元NumPy配列です。
  • np.linalg.solve() 関数を使用して、係数行列 A と右辺ベクトル b から方程式を解きます。

2. グラフのプロット:

  • n_values は、行列の次元を$2$から$10$まで変化させるための配列です。
  • plt.figure() 関数で新しいプロットを作成し、図のサイズを指定します。
  • for ループを使用して、各 n について tridiagonal_matrix_eq() を呼び出し、解を計算します。
  • plt.plot() 関数を使用して、解のグラフをプロットします。
    各解は、インデックス番号に対応する x 軸の値に対してプロットされます。
  • plt.xlabel()、plt.ylabel()、plt.title() 関数を使用して、軸ラベルとタイトルを設定します。
  • plt.legend() 関数を使用して、各解に対する凡例を追加します。
  • plt.grid(True) でグリッドを表示し、plt.show() でグラフを表示します。

このコードは、トリッツ行列方程式の解を計算し、さまざまな行列の次元に対する解をグラフ化しています。

行列の次元が増加するにつれて、解がどのように振る舞うかを視覚的に理解するのに役立ちます。

結果解説

[実行結果]

このグラフは、トリッツ行列方程式の解を示しています。
トリッツ行列方程式は、対角成分とその両隣の要素だけが非ゼロである特別な行列に対する連立方程式です。

横軸は行列の次元を表し、縦軸は方程式の解の値を示しています。
各曲線は、行列の次元が異なる場合の解を表しています。
次元が大きくなるにつれて、方程式の解がどのように振る舞うかを観察できます。

このグラフを見ると、行列の次元が増加するにつれて、解の振る舞いがどのように変化するかがわかります。
特に、次元が増えると、解の値が収束する傾向があることが観察されるかもしれません。
これは、行列の次元が増加するにつれて、対角成分に対する非ゼロの要素の影響が強まるためです。

このグラフは、トリッツ行列方程式の理解を深めるのに役立ちます。
行列の次元が増加すると、方程式の解がどのように振る舞うかを視覚的に理解するのに役立ちます。