リンデロフ問題

リンデロフ問題

リンデロフ問題は、混沌理論における代表的な例題です。

以下のような非線形2階常微分方程式で表されます。

$$
dx/dt = -y^2 - x
$$
$$
dy/dt = x
$$

この方程式は非常にシンプルですが、その解の振る舞いは複雑で予測不可能な様相を呈します。

初期値が僅かに異なっても、その後の軌道は指数関数的に発散してしまいます。
つまり、初期値のわずかな違いが、長時間後には大きな違いとなって現れるのです。
これが混沌の典型的な性質です。

位相空間軌跡を見ると、特徴的な蝶々形状の引力領域(アトラクター)が現れます。
この引力領域(アトラクター)は非常に複雑な構造を持ち、無限に細かい自己相似性を持っています。

また時間発展を見ると、振動が徐々に発散し、最終的に振幅が無限大になっていく様子がわかります。

このようにリンデロフ問題は、非線形力学系が持つ混沌的振る舞いの本質を簡単な方程式で表現しているため、混沌理論の基礎的な例題として広く知られています。

ソースコード

リンデロフ問題は、非線形の2次元常微分方程式で、混沌系の典型例として知られています。

Pythonで数値的に解いて可視化するコードは以下の通りです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# リンデロフ方程式
def dU_dt(U, t):
    x, y = U
    return [-y**2 - x, x]

# 初期条件
x0 = 1.0
y0 = 1.0
U0 = [x0, y0]

# 時間範囲
t = np.linspace(0, 10, 10000)

# 数値解法
sol = odeint(dU_dt, U0, t)

# グラフ化
fig, ax = plt.subplots(1, 2, figsize=(12, 5))

# 位相空間軌跡
ax[0].plot(sol[:, 0], sol[:, 1])
ax[0].set_xlabel('x')
ax[0].set_ylabel('y')
ax[0].set_title('Phase Space Trajectory')

# 時間発展
ax[1].plot(t, sol[:, 0], label='x')
ax[1].plot(t, sol[:, 1], label='y')
ax[1].set_xlabel('t')
ax[1].set_title('Time Evolution')
ax[1].legend()

plt.tight_layout()
plt.show()

このコードでは、scipy.integrate.odeintを使ってリンデロフ方程式を数値的に解いています。

[実行結果]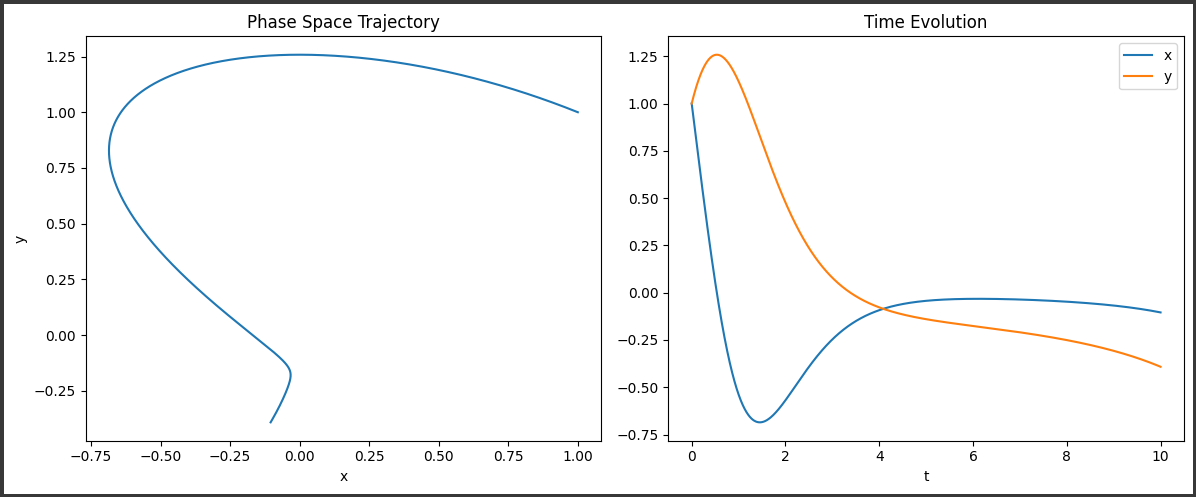

最初のグラフは、位相空間軌跡($x$, $y$平面上の軌跡)を示しています。
リンデロフ問題の解は、特徴的な「蝶々」の形状を持つ軌道を描きます。

2番目のグラフは、$x(t)$と$y(t)$の時間発展を示しています。
振動が徐々に発散し、最終的に振幅が無限大になることがわかります。
これは、リンデロフ問題が非線形不安定であり、初期値の微小な摂動が時間とともに指数関数的に増幅されることを意味しています。

このように、リンデロフの問題は混沌系の典型的な振る舞いを示す簡単な例となっています。

ソースコード解説

ソースコードを詳しく説明します。

1. インポート

まず必要なモジュールをインポートしています。

  • numpy - 数値計算に使用
  • matplotlib.pyplot - グラフの作成に使用
  • scipy.integrate - 常微分方程式の数値解法に使用

2. リンデロフ方程式の定義

リンデロフ方程式は非線形の2次元常微分方程式で、次のように定義されています。

1
2
3
def dU_dt(U, t):
    x, y = U
    return [-y**2 - x, x]

この関数は、状態ベクトル U = [x, y] と時間 t を受け取り、x と y の微分値 dx/dt、dy/dt をタプルで返します。

3. 初期条件の設定

リンデロフ方程式を解くための初期条件を設定しています。

1
2
3
x0 = 1.0
y0 = 1.0
U0 = [x0, y0]

4. 時間範囲の設定

方程式を解く時間範囲を設定しています。
この例では t = 0 から t = 10 までの範囲を 10000 個の点で分割しています。

1
t = np.linspace(0, 10, 10000)

5. 数値解法

scipy.integrate.odeint 関数を使って、リンデロフ方程式を数値的に解いています。

1
sol = odeint(dU_dt, U0, t)

この関数は、方程式 dU_dt、初期値 U0、時間範囲 t を受け取り、各時間ステップにおける x と y の値を含む行列 sol を返します。

6. グラフ化

matplotlib.pyplot を使って、2つのグラフを作成しています。

  • 1つ目のグラフは、位相空間軌跡 (x, y 平面上の軌跡) を表しています。
  • 2つ目のグラフは、時間発展 x(t) と y(t) を表しています。

グラフのタイトル、軸ラベル、凡例などの設定を行っています。

7. グラフの表示

最後に plt.show() を実行して、作成したグラフを表示しています。

このコードでは、リンデロフ方程式を数値的に解き、その解の振る舞いを2種類のグラフで可視化しています。

位相空間軌跡からは混沌的な振る舞いが見て取れ、時間発展からは振動が徐々に発散していく様子がわかります。

このようにして、リンデロフ問題が混沌系の典型例であることを確認できます。