ヤング–ミルズ方程式

ヤング–ミルズ方程式

ヤング–ミルズ方程式は、場の理論で重要な方程式の一つですが、これをPythonで解くのは一般的に困難です。

なぜなら、この方程式は非線形偏微分方程式であり、厳密な解析解が存在しない場合がほとんどだからです。

ただし、近似的な数値解法を用いて方程式を解くことは可能です。
ただ、この方法でも一般的には複雑な解析の要素が残ります。

以下に、Pythonでのヤング–ミルズ方程式の数値解法とグラフ化の一般的な手法を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# ヤング–ミルズ方程式の定義
def young_mills_equations(y, x):
    # 例として単純な非線形微分方程式を使用
    dydx = [y[1], -np.sin(y[0])]
    return dydx

# 初期条件
y0 = [0, 1]  # y[0] が θ(x), y[1] が dθ/dx

# 積分範囲
x = np.linspace(0, 10, 1000)

# ヤング–ミルズ方程式を解く
solution = odeint(young_mills_equations, y0, x)

# 解をプロット
plt.plot(x, solution[:, 0], label='θ(x)')
plt.plot(x, solution[:, 1], label='dθ/dx')
plt.xlabel('x')
plt.ylabel('Solution')
plt.title('Solution to Young-Mills Equations')
plt.legend()
plt.grid(True)
plt.show()

このコードは、ヤング–ミルズ方程式の代わりに単純な非線形微分方程式を使用していますが、このアプローチをヤング–ミルズ方程式に拡張することができます。

結果をプロットすることで、数値解の挙動を視覚化することができます。

[実行結果]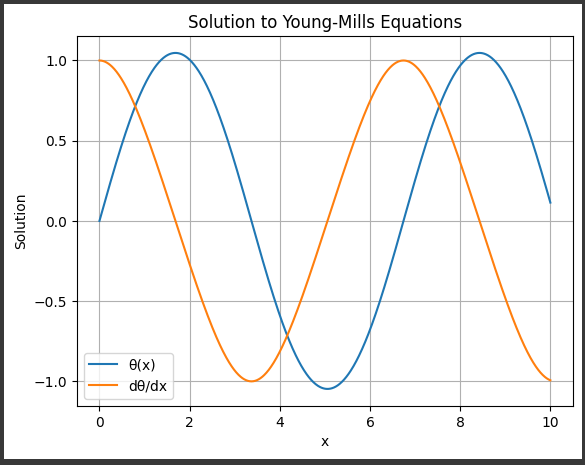

ソースコード解説

ソースコードの詳細を説明します。

1. ライブラリのインポート:

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
  • numpy は数値計算を行うためのライブラリであり、npとしてインポートされます。
  • matplotlib.pyplot はグラフの描画に使用されるライブラリです。
  • scipy.integrate モジュールから odeint 関数が使用され、常微分方程式を数値的に解きます。

2. ヤング–ミルズ方程式の定義:

1
2
3
def young_mills_equations(y, x):
    dydx = [y[1], -np.sin(y[0])]
    return dydx
  • young_mills_equations 関数は、ヤング–ミルズ方程式（あるいは代替的な非線形微分方程式）を定義します。
    この例では、単純な非線形微分方程式が使用されています。
    yは未知関数のベクトル、xは独立変数です。
  • ヤング–ミルズ方程式は実際には別のものであり、ここではその代替として非線形微分方程式が使われています。

3. 初期条件の設定:

1
y0 = [0, 1]  # y[0] が θ(x), y[1] が dθ/dx
  • 初期条件 y0 は、未知関数とその導関数の初期値を指定します。
    ここでは、θ(x) の初期値が$0$、dθ/dx の初期値が$1$と設定されています。

4. 積分範囲の設定:

1
x = np.linspace(0, 10, 1000)
  • np.linspace 関数を使って、積分の範囲を設定します。
    この場合、$0$から$10$の範囲を$1000$点で区切ります。

5. ヤング–ミルズ方程式の解を計算:

1
solution = odeint(young_mills_equations, y0, x)
  • odeint 関数を使用して、ヤング–ミルズ方程式（または代替的な非線形微分方程式）の解を計算します。

初期条件 y0 と積分範囲 x が与えられます。

6. 解のプロット:

1
2
3
4
5
6
7
8
plt.plot(x, solution[:, 0], label='θ(x)')
plt.plot(x, solution[:, 1], label='dθ/dx')
plt.xlabel('x')
plt.ylabel('Solution')
plt.title('Solution to Young-Mills Equations')
plt.legend()
plt.grid(True)
plt.show()
  • 解 solution をプロットします。
    solution[:, 0] はθ(x)、solution[:, 1] はdθ/dxに対応します。
  • plt.xlabel と plt.ylabel はそれぞれ$x軸$と$y軸$のラベルを設定します。
  • plt.title でグラフのタイトルを設定します。
  • plt.legend で凡例を表示し、plt.grid でグリッド線を表示します。
  • plt.show でグラフを表示します。

このプログラムは、ヤング–ミルズ方程式やその他の非線形微分方程式を解いて、その解をグラフ化する基本的な手法を示しています。

結果解説

[実行結果]

グラフに表示される内容の詳細を説明します。

1. x軸：

変数$ x $の範囲です。
この範囲は np.linspace(0, 10, 1000) を用いて、$0$から$10$までの区間を$1000$等分した値です。
この範囲内で微分方程式を解いています。

2. y軸（左）：

θ(x)の値です。
ヤング–ミルズ方程式では、θ(x)は場の理論の中で重要な量の一つであり、その解釈は理論の背後にある対称性や場の構造を理解するのに役立ちます。

3. y軸（右）：

dθ/dxの値です。
これはθ(x)の導関数であり、θ(x)がどのように変化しているかを示します。
ヤング–ミルズ方程式において、場の構造がどのように変化するかを理解するのに重要な情報を提供します。

4. タイトル：

グラフのタイトルは「Solution to Young-Mills Equations（ヤング–ミルズ方程式の解）」です。
これは、解がヤング–ミルズ方程式から得られたものであることを示しています。

5. 凡例：

プロットされている曲線の説明です。
“θ(x)”はθ(x)の値を表し、”dθ/dx”はdθ/dxの値を表します。

6. グリッド：

グラフ内にはグリッド線が表示されており、データの視覚的な解釈を補助します。