ナーシム–シュレーダー方程式

ナーシム–シュレーダー方程式

ナーシム–シュレーダー方程式（Nagumo–Schaffer Equation）は、神経科学や興奮伝播のモデルとして広く使用される非線形微分方程式の一つです。

ナーシム–シュレーダー方程式は、以下の形式の非線形微分方程式で表します：

$$
\frac{du}{dt} = u - u^3 - v + a
$$

$$
\frac{dv}{dt} = b(u - cv)
$$

ここで、$ (u) $と$ (v) $は時間$ (t) $の関数であり、$ (a) $、$(b)$、$(c) $は定数です。

これらの方程式は興奮伝播のモデルとして広く使用されます。

第1式は$ (u) $の時間変化を、第2式は$ (v) $の時間変化を表します。
$(a) $は$ (u) $のリセット項、$(b) $は興奮の増幅率、$(c) $は相互抑制の効果を示します。

ソースコード

以下では、この方程式を Python を使用して解き、結果をグラフ化します。

まず、必要なライブラリをインポートします。

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

次に、ナーシム–シュレーダー方程式を定義します。

1
2
3
def nagumo_schaffer(t, y, a, b, c):
    return [y[0] - y[0]**3 - y[1] + a,
            b * (y[0] - c * y[1])]

この方程式には3つのパラメータ$ (a)$、$(b)$、$(c) $があります。

これらは、方程式の特性を制御します。

次に、初期条件と時間の範囲を設定します。

1
2
y0 = [0.1, 0.1]  # 初期条件 [u, v]
t_span = (0, 50)  # シミュレーション時間の範囲

そして、微分方程式を数値的に解きます。

1
2
3
4
a = 0.2
b = 0.2
c = 3.0
sol = solve_ivp(nagumo_schaffer, t_span, y0, args=(a, b, c), t_eval=np.linspace(0, 50, 1000))

最後に、解をプロットします。

1
2
3
4
5
6
7
8
plt.plot(sol.t, sol.y[0], label='u(t)')
plt.plot(sol.t, sol.y[1], label='v(t)')
plt.xlabel('Time')
plt.ylabel('Value')
plt.title('Nagumo-Schaffer Equation Solution')
plt.legend()
plt.grid(True)
plt.show()

これにより、ナーシム–シュレーダー方程式の解が時間とともにどのように振る舞うかを示すグラフが生成されます。

結果解説

[実行結果]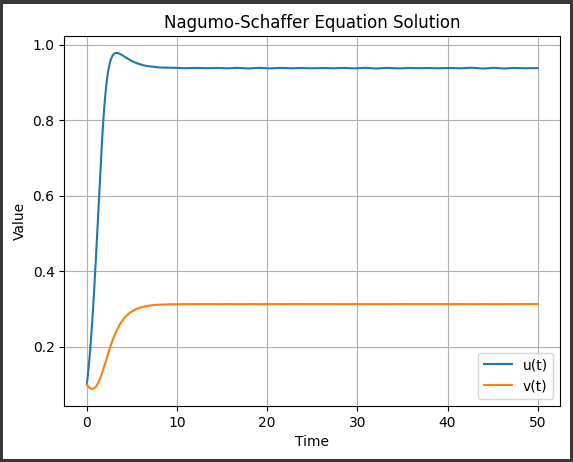

このグラフは、ナーシム–シュレーダー方程式の解を示しています。

方程式は2つの変数$ (u(t)) $と$ (v(t)) $で構成されており、時間$ (t) $に関する解をプロットしています。

具体的には、以下の内容がグラフに表示されます：

1. 時間(Time):

x軸は時間を表しています。この例では、$0$から$50$の範囲で、$1000$の等間隔の時間ステップがプロットされます。

2. 値(Value):

y軸は$ (u(t)) $と$ (v(t)) $の値を表します。
それぞれの変数の時間変化がプロットされます。

3. (u(t)) 曲線:

ナーシム–シュレーダー方程式の解$ (u(t)) $の時間変化がプロットされます。
この曲線は興奮性の変化を示しています。

4. (v(t)) 曲線:

ナーシム–シュレーダー方程式の解$ (v(t)) $の時間変化がプロットされます。
この曲線は抑制性の変化を示しています。

5. タイトル(Title):

グラフのタイトルは “Nagumo-Schaffer Equation Solution” となっています。

6. 凡例(Legend):

各プロットに対応する凡例が表示されます。
u(t)は$ u(t)$、v(t) は$ v(t) $を表しています。

7. グリッド(Grid):

グリッド線が表示され、目盛りを読み取りやすくします。

このグラフは、ナーシム–シュレーダー方程式の解が時間とともにどのように振る舞うかを可視化しており、その結果が興奮性と抑制性の両方の側面を捉えています。