フェルマーの最終定理

フェルマーの最終定理

フェルマーの最終定理は「$n>2$のとき、$x^n + y^n = z^n$を満たす自然数$x,y,z$は存在しない」というものです。

これをPythonで表現し、グラフ化するには以下のようなコードを使うことができます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import matplotlib.pyplot as plt
import numpy as np

# パラメータ設定
n = 3  # 検証する指数
max_val = 100  # x,y,zの最大値

# グリッド上の全ての点をチェック
x = np.arange(max_val)
y = np.arange(max_val)
X, Y = np.meshgrid(x, y)
Z = X**n + Y**n

# 方程式を満たす点をプロット
plt.figure(figsize=(8, 6))
plt.scatter(X[Z <= max_val**n], Y[Z <= max_val**n], s=1, c='b')
plt.scatter(X[Z > max_val**n], Y[Z > max_val**n], s=1, c='r')
plt.xlim(0, max_val)
plt.ylim(0, max_val)
plt.title(f'Fermat\'s Last Theorem (n={n})')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

このコードでは、指数$n$と$x$,$y$,$z$の最大値を設定できます。

そして、グリッド上の全ての$(x,y)$の組み合わせについて、$x^n + y^n$が$max＿val^n$を超えるかどうかをチェックしています。

方程式を満たす点$(x^n + y^n <= max＿val^n)$は青色で、満たさない点は赤色でプロットされます。

グラフの例(n=3, max_val=100)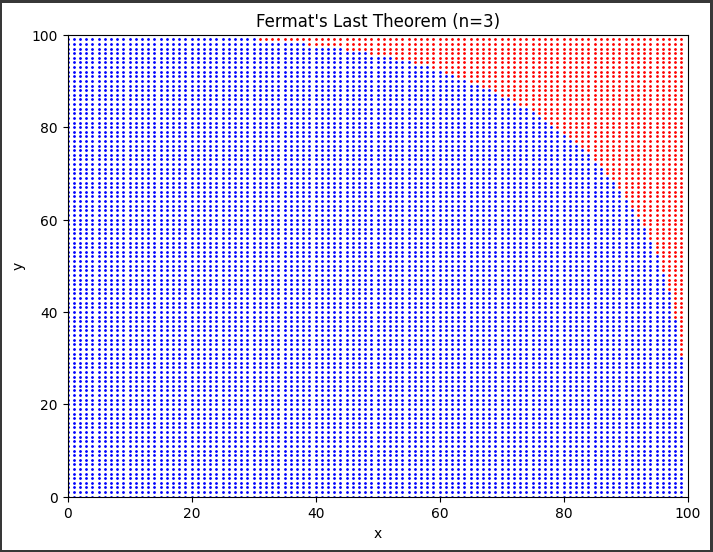

このグラフから、$n=3$の場合、$x^3 + y^3 = z^3$を満たす自然数の組$(x,y,z)$が存在しないことが分かります。
$max＿val$を大きくすれば、より大きな値についてもフェルマーの最終定理が成り立つことを確認できます。

ソースコード解説

ソースコードを詳しく説明します。

1. ライブラリのインポート

1
2
import matplotlib.pyplot as plt
import numpy as np
  • matplotlib.pyplot: グラフを描画するためのライブラリ
  • numpy: 数値計算ライブラリ

2. パラメータ設定

1
2
n = 3  # 検証する指数
max_val = 100  # x,y,zの最大値
  • $n$には検証したい指数(この例では$n=3$)を設定します
  • $max_val$には、$x$,$y$,$z$の最大値を設定します

3. グリッド上の全ての点をチェック

1
2
3
4
x = np.arange(max_val)
y = np.arange(max_val)
X, Y = np.meshgrid(x, y)
Z = X**n + Y**n
  • $x, y$にそれぞれ$0$から$max＿val-1$までの値を格納した1次元NumPy配列を作成
  • np.meshgrid(x, y)で、$x$,$y$の全ての組み合わせからなる2次元グリッドX,Yを生成
  • X**n + Y**nで、各グリッド点$(x,y)$における$x^n + y^n$の値を計算し、$Z$にNumPy配列として格納

4. 方程式を満たす点をプロット

1
2
3
4
5
6
7
8
9
plt.figure(figsize=(8, 6))
plt.scatter(X[Z <= max_val**n], Y[Z <= max_val**n], s=1, c='b')
plt.scatter(X[Z > max_val**n], Y[Z > max_val**n], s=1, c='r')
plt.xlim(0, max_val)
plt.ylim(0, max_val)
plt.title(f'Fermat\'s Last Theorem (n={n})')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
  • plt.figure(figsize=(8, 6))で新しい図を作成し、サイズを指定
  • 1つ目のplt.scatter():
    • X[Z <= max_val**n]は、$x^n + y^n <= max＿val^n$を満たす$x$の値
    • Y[Z <= max_val**n]は、$x^n + y^n <= max＿val^n$を満たす$y$の値
    • s=1で点のサイズを1に設定
    • c=’b’で点の色を青に設定
  • 2つ目のplt.scatter():
    • X[Z > max_val**n]は、$x^n + y^n > max_val^n$を満たす$x$の値
    • Y[Z > max_val**n]は、$x^n + y^n > max_val^n$を満たす$y$の値
    • s=1で点のサイズを1に設定
    • c=’r’で点の色を赤に設定
  • plt.xlim(0, max_val)、plt.ylim(0, max_val)でx軸、y軸の範囲を設定
  • plt.title(f’Fermat's Last Theorem (n={n})’)でグラフのタイトルを設定
  • plt.xlabel(‘x’)、plt.ylabel(‘y’)で軸ラベルを設定
  • plt.show()でグラフを表示

このコードでは、指定した範囲の全ての$(x,y)$の組み合わせについて、$x^n + y^n$の値が$max＿val^n$を超えるかどうかをチェックし、超えない点(方程式を満たす点)を青色で、超える点を赤色でプロットしています。

また、適切な軸範囲、タイトル、ラベルを設定してグラフを描画しています。

結果解説

[実行結果]

このグラフには以下の情報が表示されています。

1. 点の色

青い点: $x^n + y^n $の値が$max＿val^n$以下の$(x,y)$の組
赤い点: $x^n + y^n $の値が$max＿val^n$を超える$(x,y)$の組

2. 軸

x軸: x値 ($0$から$max＿val$まで)
y軸: y値 ($0$から$max＿val$まで)

3. タイトル

グラフのタイトルには “Fermat’s Last Theorem (n=3)” と表示されています。
つまり、このグラフはフェルマーの最終定理を$n=3$の場合について可視化したものです。

4. 点の分布

原点$(0, 0)$を中心に、青い点が放射状に広がっています。
赤い点は原点から離れた領域に存在しています。
これは、小さな値の$x$,$y$に対しては$x^3 + y^3$が$max＿val^3$以下になりやすいが、$x$,$y$が大きくなるにつれて$max＿val^3$を超えやすくなることを示しています。

5. グラフの形状

点の分布から、青い領域は滑らかなカーブ状の境界線を持っていることが分かります。
この境界線は、$x^3 + y^3 = max＿val^3 $という3次曲面を表しています。

6. 点の密度

原点付近では青い点が密集していますが、原点から離れるにつれて点の密度が低下しています。
これは、小さな値の$x$,$y$の組み合わせの方が多いためです。

このグラフを見ることで、$n=3$の場合にはフェルマーの最終定理が視覚的に裏付けられていることが分かります。

青い点は$x^n + y^n = z^n$を満たす可能性のある$(x,y)$の組を表し、赤い点はその組み合わせが存在しないことを示しています。