ジュリア集合

3月 16, 2024

ジュリア集合

ジュリア集合は、複素関数の反復による軌道の振る舞いを示す集合です。

ジュリア集合の収束性の条件をPythonで可視化するコードを書きます。

import numpy as np
import matplotlib.pyplot as plt

def julia(c, x, y, max_iter=100):
    z = x + 1j * y
    for i in range(max_iter):
        z = z ** 2 + c
        if np.abs(z) > 2:
            return i
    return max_iter

def plot_julia(c, zoom=1, x_range=(-2, 2), y_range=(-1.5, 1.5), max_iter=100):
    x = np.linspace(x_range[0] / zoom, x_range[1] / zoom, 1000)
    y = np.linspace(y_range[0] / zoom, y_range[1] / zoom, 1000)
    X, Y = np.meshgrid(x, y)

    Z = np.zeros_like(X, dtype=int)
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Z[i, j] = julia(c, X[i, j], Y[i, j], max_iter)

    plt.figure(figsize=(10, 8))
    plt.imshow(Z, cmap='hot', extent=(x_range[0], x_range[1], y_range[0], y_range[1]))
    plt.colorbar()
    plt.xlabel('Re(c)', fontsize=14)
    plt.ylabel('Im(c)', fontsize=14)
    plt.title(f'Julia Set for c={c:.2f}', fontsize=16)
    plt.show()

# 例: c = -0.8 + 0.156j のジュリア集合
plot_julia(-0.8 + 0.156j, zoom=1, max_iter=100)

このコードでは、まず julia 関数を定義しています。
この関数は、与えられた複素数 c と初期値 x, y について、反復 z = z**2 + c を最大 max_iter 回行い、発散するまでの反復回数を返します。

次に、plot_julia 関数を定義しています。
この関数は、与えられた c について、ジュリア集合をプロットします。
まず、x と y の範囲を設定し、それらの組み合わせについて julia 関数を呼び出して発散までの反復回数を求めます。
その結果を行列 Z に格納し、plt.imshow でプロットしています。

最後に、plot_julia(-0.8 + 0.156j, zoom=1, max_iter=100) と指定して、ジュリア集合をプロットしています。

実行結果は、複素平面上のジュリア集合を可視化した画像になります。

[実行結果]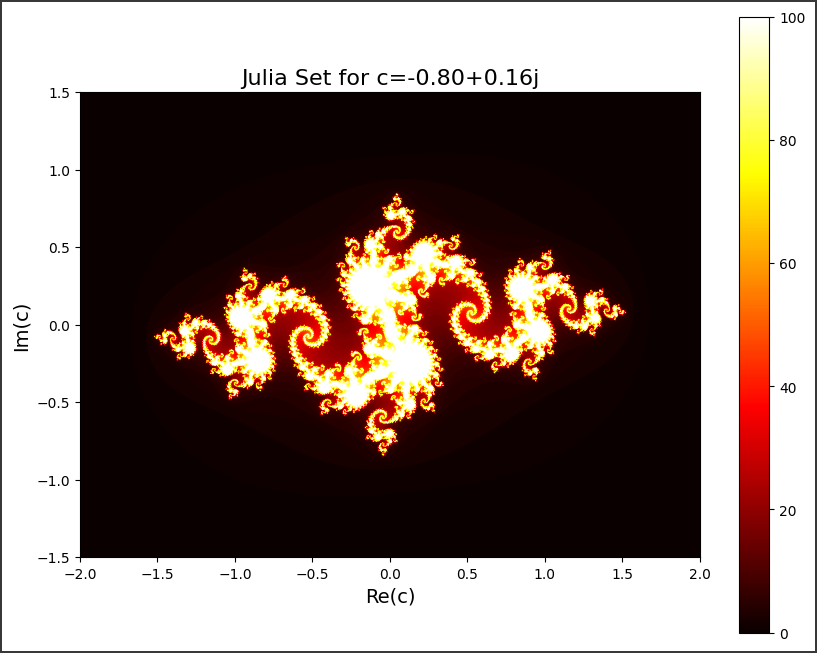

色が濃いほど発散までの反復回数が多く、白い部分が発散しない領域(ジュリア集合自体)になります。
このジュリア集合は、フラクタル構造を持っていることがわかります。

ジュリア集合は、カオス理論や複素動力学系の研究で重要な役割を果たしています。
また、その美しいフラクタル構造から、コンピュータグラフィックスなどでも活用されています。

ソースコード解説

コードを詳しく説明します。

1 : ジュリア集合の計算関数

def julia(c, x, y, max_iter=100):
    z = x + 1j * y
    for i in range(max_iter):
        z = z ** 2 + c
        if np.abs(z) > 2:
            return i
    return max_iter

julia関数は、与えられた複素数cと初期値(x, y)について、反復z = z**2 + cを最大max_iter回行います。
反復の過程で$z$の絶対値が$2$を超えれば(発散した場合)、その反復回数を返します。
max_iter回まで発散しなければmax_iterを返します。

2 : ジュリア集合の可視化関数

def plot_julia(c, zoom=1, x_range=(-2, 2), y_range=(-1.5, 1.5), max_iter=100):
    x = np.linspace(x_range[0] / zoom, x_range[1] / zoom, 1000)
    y = np.linspace(y_range[0] / zoom, y_range[1] / zoom, 1000)
    X, Y = np.meshgrid(x, y)

    Z = np.zeros_like(X, dtype=int)
    for i in range(X.shape[0]):
        for j in range(X.shape[1]):
            Z[i, j] = julia(c, X[i, j], Y[i, j], max_iter)

    plt.figure(figsize=(10, 8))
    plt.imshow(Z, cmap='hot', extent=(x_range[0], x_range[1], y_range[0], y_range[1]))
    plt.colorbar()
    plt.xlabel('Re(c)', fontsize=14)
    plt.ylabel('Im(c)', fontsize=14)
    plt.title(f'Julia Set for c={c:.2f}', fontsize=16)
    plt.show()

plot_julia関数は、与えられたcについてジュリア集合をプロットします。
まず、$x$、$y$の範囲を設定し、それらの組み合わせについてjulia関数を呼び出します。
結果をZ行列に格納し、plt.imshowでプロットします。
軸ラベル、タイトル、カラーバーを設定し、グラフを表示します。

3 : プログラムの実行

1 2	# 例: c = -0.8 + 0.156j のジュリア集合 plot_julia(-0.8 + 0.156j, zoom=1, max_iter=100)

plot_julia関数を呼び出し、c = -0.8 + 0.156jのジュリア集合をプロットしています。
zoomは$1$(デフォルト)、max_iterは100回に設定されています。

このコードは、ジュリア集合の計算と可視化を行っています。主な手順は以下の通りです。

julia関数で、与えられた$c$と初期値$ (x, y) $について、反復z = z**2 + cを行い、発散するまでの反復回数を求めます。
plot_julia関数で、複素平面上の$(x, y)$の範囲を設定し、それぞれの点についてjulia関数を呼び出します。
得られた発散までの反復回数を行列Zに格納します。
行列Zをプロットし、発散速度(反復回数)を色で可視化します。
軸ラベル、タイトル、カラーバーを設定してグラフを表示します。

最終的に、ジュリア集合の複雑で自己相似的な構造を可視化したグラフが得られます。

結果解説

[実行結果]

このグラフはジュリア集合の様子を可視化したものです。

グラフの詳細を説明します。

グラフの横軸は複素数$c$の実部を、縦軸は$c$の虚部を表しています。
つまり、複素平面上の点がプロットされています。
背景の色は、ある初期値$(x, y)$からジュリア集合の反復$z = z**2 + c$を行ったときの発散する速さを表しています。
赤や黄色は早く発散し、青や紫は遅く発散することを意味します。
一方で、白い領域は発散しない点の集まりです。
これがジュリア集合自体を表しています。
ジュリア集合の形状は、与えられた$c$の値によって大きく異なります。
このグラフでは$c = -0.8 + 0.156j$が使われています。
ジュリア集合自体は非常に複雑な構造を持ち、フラクタル的な自己相似性が見られます。
つまり、拡大するとほぼ同じ模様が現れる性質があります。
白い領域(ジュリア集合)の周りに同心円状の渦巻き模様があり、そこから外に向かうにつれて発散速度が速くなっていきます。
グラフ右側のカラーバーは、発散速度(反復回数)と色の対応関係を示しています。

このように、ジュリア集合は複素動力学系における重要な概念で、それ自体が不規則でフラクタル的な美しい構造を持っています。

この可視化により、ジュリア集合の様々な性質を確認できます。