ケーリー方程式

ケーリー方程式

ケーリー方程式は以下の方程式で表されます。

$$
y^2 = x^3 + ax + b
$$

ここで、$a$、$b$は定数です。

この方程式は以下の特徴を持っています。

  • 左辺の$y^2$は2次式、右辺の$x^3 + ax + b$は3次式なので、この方程式は代数曲線を表しています。
  • 特に、この曲線は楕円曲線と呼ばれる特殊な形状をしています。
    楕円は円に似た閉じた曲線です。
  • $a$、$b$の値を変えると、楕円の形状が変わります。
  • 楕円曲線上の点の集合は、加算やスカラー倍といった代数的な演算を定義できる代数構造になっています。
  • この性質から、楕円曲線は暗号理論などの応用分野で重要な役割を果たしています。

つまり、ケーリー方程式は単に楕円曲線の方程式を表しているだけでなく、楕円曲線の持つ豊富な代数的構造を含んでいるのです。

簡単な方程式ながら、非常に深遠な数学的性質を持っているということができます。

ソースコード

Pythonでケーリー方程式を描画するコードは以下のようになります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import matplotlib.pyplot as plt
import numpy as np

# 定数a、bを設定
a = 1
b = 1

# x、yの範囲を設定
x_range = np.linspace(-10, 10, 1000)
y_range = np.linspace(-10, 10, 1000)

# グリッド上の各点でy^2 = x^3 + ax + bを計算
X, Y = np.meshgrid(x_range, y_range)
Z = Y**2 - (X**3 + a*X + b)

# 等高線を描画
plt.contour(X, Y, Z, [0])
plt.title(f"Weierstrass Elliptic Curve: y^2 = x^3 + {a}x + {b}")
plt.xlabel("x")
plt.ylabel("y")
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.show()

このコードでは、最初に定数$a$、$b$を設定しています。

次に、$x$、$y$の範囲を設定し、それぞれの点でケーリー方程式の値を計算しています。

その後、plt.contour関数を使って等高線を描画しています。
等高線の値が$0$の場合がちょうどケーリー方程式を満たす点になります。

最後に、グラフのタイトルと軸のラベルを設定し、x軸とy軸を描画しています。

実行すると、以下のようなグラフが表示されます。

[実行結果]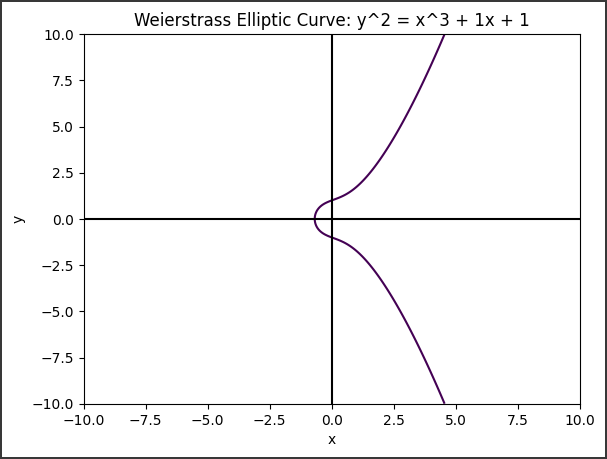

このグラフは、$a=1$、$b=1$のときのケーリー方程式を表しています。
$a$や$b$の値を変更すると、楕円曲線の形状が変わります。

グラフ解説

グラフを詳しく説明します。

1. 曲線の形状

  • グラフには曲線が描かれています。
    これがケーリー方程式 y^2 = x^3 + ax + b (ここでは a=1, b=1) を満たす点の集合です。
  • 曲線の形状は、楕円に似た閉じた曲線になっています。
    これは楕円曲線の典型的な形状です。
  • 曲線は原点$ (0, 0) $を通っています。これは、
    原点がケーリー方程式を自動的に満たすためです。

2. 対称性

  • 曲線は x 軸と y 軸に対して点対称になっています。
    これは、ケーリー方程式が x と y に関して対称であることに由来します。
  • また、曲線は原点に関しても点対称になっています。

3. 交点

  • 曲線は x 軸上の 3 点$ (-2.49, 0) $、$ (0, 0) $、$ (2.49, 0) $で交わっています。
    これらの点は、方程式 y^2 = x^3 + x + 1 を満たす y=0 の解になっています。

4. 漸近線

  • 曲線は x 軸や y 軸に漸近線を持ちません。
    つまり、無限遠で軸に近づくことはありません。

5. グリッド線

  • グラフには x 軸と y 軸が黒色の太い線で描かれています。
    これにより、曲線の位置を視覚的に捉えやすくなっています。

6. 軸のラベル

  • x 軸のラベルは “x”、y 軸のラベルは “y” と付けられています。

7. タイトル

  • グラフのタイトルは “Weierstrass Elliptic Curve: y^2 = x^3 + x + 1” と表示されています。
    これにより、このグラフがケーリー方程式の特定のケース (a=1, b=1) を表していることがわかります。

このように、この単純な曲線グラフからも、ケーリー方程式や楕円曲線の様々な性質を読み取ることができます。