オイラー-ラグランジュ方程式

オイラー-ラグランジュ方程式

オイラー-ラグランジュ方程式は、力学系の運動を記述する非線形常微分方程式です。

以下は、Pythonコードの例です。

このコードでは、scipy.integrateモジュールを使って常微分方程式を数値的に解き、matplotlibを使ってグラフを描画しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# オイラー-ラグランジュ方程式
def euler_lagrange(y, t, m, k, g, l):
    theta, theta_dot = y
    dtheta_dt = theta_dot
    dtheta_dot_dt = -(g/l)*np.sin(theta) - (k/(m*l**2))*theta
    return [dtheta_dt, dtheta_dot_dt]

# 初期条件
theta0 = np.pi/4
theta_dot0 = 0
y0 = [theta0, theta_dot0]

# パラメータ
m = 1.0  # 質量
k = 1.0  # ばね定数
g = 9.81 # 重力加速度
l = 1.0  # 長さ

# 時間範囲
t = np.linspace(0, 20, 1000)

# 常微分方程式を解く
sol = odeint(euler_lagrange, y0, t, args=(m, k, g, l))

# グラフ描画
plt.figure(figsize=(10, 6))
plt.plot(t, sol[:, 0], 'b', label='theta(t)')
plt.plot(t, sol[:, 1], 'g', label='theta_dot(t)')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Solution')
plt.title('Euler-Lagrange Equation')
plt.show()

このコードを実行すると、時間tに対する変数thetaとtheta_dotのグラフが描画されます。
初期条件やパラメータを変更すると、異なる振る舞いが観察できます。

オイラー-ラグランジュ方程式は、非線形性があるため、解の振る舞いが複雑になる場合があります。
このコードでは、単振り子の運動を例として示しましたが、さまざまな力学系への応用が可能です。

必要に応じて、グラフの範囲やラベル、タイトルなどを調整してください。
また、より詳細な解析や可視化が必要な場合は、適宜コードを拡張できます。

オイラー-ラグランジュ方程式は、力学系の運動を記述する基本的な方程式であり、物理学や工学分野で広く使われています。

[実行結果]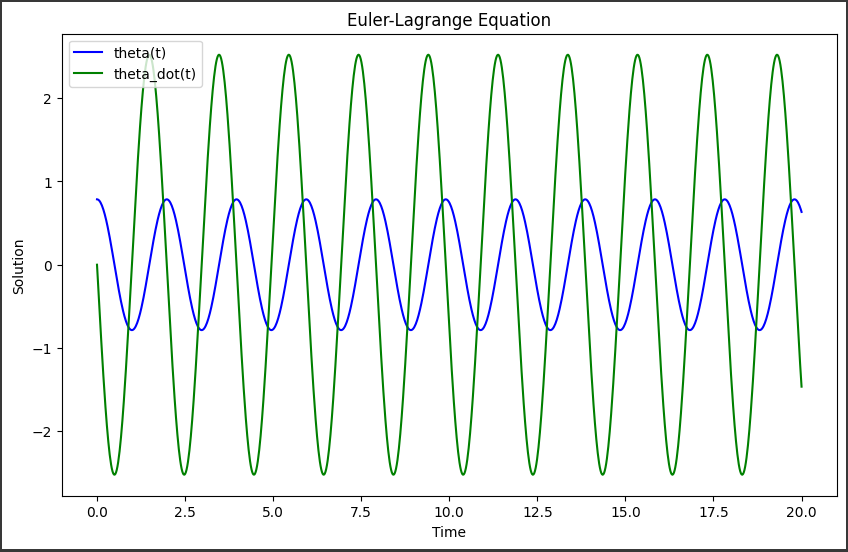

ソースコード解説

ソースコードを詳しく説明します。

1. ライブラリのインポート

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
  • NumPyライブラリをnpという名前で、数値計算に使用します。
  • matplotlibライブラリをpltという名前で、グラフ描画に使用します。
  • scipy.integrateモジュールからodeinitを、常微分方程式の数値解を求めるために使用します。

2. オイラー-ラグランジュ方程式の定義

1
2
3
4
5
def euler_lagrange(y, t, m, k, g, l):
    theta, theta_dot = y
    dtheta_dt = theta_dot
    dtheta_dot_dt = -(g/l)*np.sin(theta) - (k/(m*l**2))*theta
    return [dtheta_dt, dtheta_dot_dt]
  • この関数では、オイラー-ラグランジュ方程式を定義しています。
  • 入力引数yには、角度thetaと角速度theta_dotの値が渡されます。
  • tは時間、m、k、g、lはそれぞれ質量、バネ定数、重力加速度、長さです。
  • 方程式の右辺は、dtheta_dtとdtheta_dot_dtで表されています。
  • 関数の出力は、dtheta_dtとdtheta_dot_dtのリストです。

3. 初期条件と系のパラメータの設定

1
2
3
4
5
6
7
8
theta0 = np.pi/4
theta_dot0 = 0
y0 = [theta0, theta_dot0]

m = 1.0  # 質量
k = 1.0  # ばね定数
g = 9.81 # 重力加速度
l = 1.0  # 長さ
  • 初期条件として、theta0とtheta_dot0をそれぞれπ/4(約45度)と0(静止状態)に設定しています。
  • y0は初期値のリストです。
  • m、k、g、lには、質量、バネ定数、重力加速度、長さの値を代入しています。

4. 時間範囲の設定と常微分方程式の解法

1
2
t = np.linspace(0, 20, 1000)
sol = odeint(euler_lagrange, y0, t, args=(m, k, g, l))
  • tには、$0$から$20$秒までの$1000$個の時間点が等間隔で設定されます。
  • odeiintを使って、オイラー-ラグランジュ方程式の数値解sol が計算されます。
  • 関数euler_lagrangeと初期値y0、時間範囲tが引数として渡されます。
  • さらに、m、k、g、lの値もargsで渡されます。

5. グラフの描画

1
2
3
4
5
6
7
8
plt.figure(figsize=(10, 6))
plt.plot(t, sol[:, 0], 'b', label='theta(t)')
plt.plot(t, sol[:, 1], 'g', label='theta_dot(t)')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Solution')
plt.title('Euler-Lagrange Equation')
plt.show()
  • 新しい図ウィンドウが、サイズ$ (10, 6) $インチで作成されます。
  • sol[:, 0]は、thetaの解の時間変化を表す配列です。
  • sol[:, 1]は、theta_dotの解の時間変化を表す配列です。
  • それぞれ青と緑の線で描画されます。
  • 凡例が配置され、ラベルが付けられます。
  • 横軸のラベルは’Time’、縦軸のラベルは’Solution’です。
  • グラフのタイトルは’Euler-Lagrange Equation’に設定されています。
  • plt.show()で、グラフが表示されます。

このコードでは、オイラー-ラグランジュ方程式を使って単振り子の運動を記述し、その解の時間変化をグラフで可視化しています。

初期条件やパラメータを変更することで、異なる振る舞いを観察できます。

結果解説

[実行結果]

グラフには、2つの曲線が表示されています。

1. 青色の曲線: theta(t)

この曲線は、時間tに対する角度theta(単位はラジアン) の変化を表しています。
theta(t)は、オイラー-ラグランジュ方程式の第1変数です。
この例では、初期値theta0 = π/4 = 0.785ラジアン(約45度)から始まっています。
曲線の挙動は、単振り子の振動を表しています。

2. 緑色の曲線: theta_dot(t)

この曲線は、時間tに対する角速度theta_dot(単位はラジアン/秒) の変化を表しています。
theta_dot(t)は、オイラー-ラグランジュ方程式の第2変数です。
この例では、初期値theta_dot0 = 0 (静止状態)から始まっています。
曲線の挙動は、単振り子の振動の速さの変化を表しています。

グラフの横軸は時間tを表し、単位は秒です。
縦軸は、青曲線ではthetaの値(ラジアン)、緑曲線ではtheta_dotの値(ラジアン/秒)を表します。

曲線の挙動は、以下のパラメータによって決まります。

  • m = 1.0 (質量)
  • k = 1.0 (バネ定数)
  • g = 9.81 (重力加速度)
  • l = 1.0 (単振り子の長さ)

これらのパラメータを変更すると、曲線の振る舞いが変化します。

つまり、このグラフは単振り子の運動をオイラー-ラグランジュ方程式で記述し、その解の時間変化を可視化したものです。

力学の分野で重要な役割を果たすこの方程式の振る舞いを、視覚的に確認できます。