回帰でも分類でも教師あり学習には正解データがあるため、定量的な評価を行うことができます。

基本的な評価指標を確認し、それぞれの指標の特徴や違いを確認していきます。

評価対象のモデルの準備

データセットと評価対象となるモデルを準備します。

まず、乳がんの診断データを読み込みデータフレームに格納します。

[Google Colaboratory]

1
2
3
4
5
6

from sklearn.datasets import load_breast_cancer
load_data = load_breast_cancer()

import pandas as pd
df = pd.DataFrame(load_data.data, columns = load_data.feature_names)
df["y"] = load_data.target

説明変数と目的変数に分け、さらに訓練データとテストデータ（7：3の割合）に分割します。

[Google Colaboratory]

1
2
3
4
5
6
7

from sklearn.model_selection import train_test_split

X= df[["mean radius","mean texture"]]
y = df["y"]
X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.3,random_state=0)

print(len(X_test))

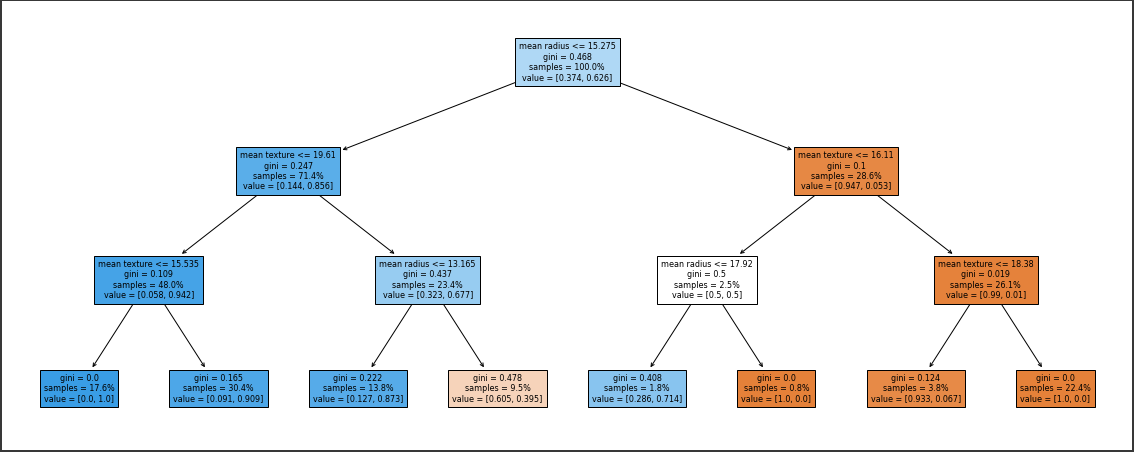
評価対象となるランダムフォレストモデルを作成し、学習を行います。（2行目）

また予測値の算出も行います。（4～5行目）

[Google Colaboratory]

1
2
3
4
5

from sklearn.ensemble import RandomForestClassifier
rf_cls = RandomForestClassifier(max_depth=3,random_state=0).fit(X_train, y_train)

y_train_pred = rf_cls.predict(X_train)
y_test_pred = rf_cls.predict(X_test)

以上でモデルの構築は完了です。

正解率

正解率は、サンプルの総数に対して何件予測を的中させたかを示すシンプルな指標です。

scikit-learnのaccuracy_scoreに実測値と予測値を渡すと、正解率を算出することができます。

[Google Colaboratory]

1
2
3
4

from sklearn.metrics import accuracy_score

print(f"訓練データ正解率：{accuracy_score(y_train,y_train_pred)}")
print(f"テストデータ正解率：{accuracy_score(y_test,y_test_pred)}")

[実行結果]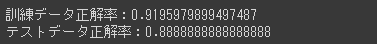

訓練データにだけ過度に適合しているということもなく、両データとも比較的高いスコアを出しており、過学習や学習不足の心配はなさそうです。

ただ正解率では、カテゴリごとの予測精度をみることができないため、より深い精度評価が必要になります。

混同行列

混同行列は、真陽性・偽陽性・真陰性・偽陽性のそれぞれのサンプル件数を可視化したマトリックス表です。

• 真陽性(TP:True Positive)
  実際に陽性で正しく陽性と予測されたサンプル
• 偽陽性(FP:False Posotove)
  実際には陽性だが陰性と予測されたサンプル
• 真陰性(TN:True Negative)
  実際に陰性で正しく陰性と予測されたサンプル
• 偽陽性(FN:False Negative)
  実際には陰性だが陽性と予測されたサンプル

混同行列を算出するためにはscikit-learnのconfusion_matrixを使用します。（5行目）

視覚的に把握しやすくするためヒートマップで結果を表示します。（7～10行目）

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10

from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
import seaborn as sns

matrix = confusion_matrix(y_test,y_test_pred)

sns.heatmap(matrix.T, square=True,annot=True)
plt.xlabel("True Label")
plt.ylabel("Pred Label")
plt.show()

混同行列を可視化することで、個別のカテゴリごとの予測精度を俯瞰してみることができ、どの部分での予測が弱いのかなども含めて直感的に把握することができます。

混同行列は多値分類でも使用することができ、カテゴリ数が多くなればなるほど視覚に訴える混同行列のメリットを享受することができます。

[実行結果]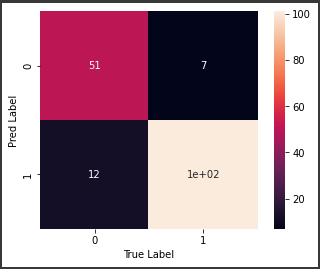

ヒートマップから、おおむね正しく予測できているようです。

ただ陽性サンプル数６３件に対して、偽陽性が１２と少し多いのが気になります。

このように混同行列はモデル精度の概観を確認するのに役立ちますが、モデルの改善やモデルの構築目的にあった評価を行うには、混同行列で算出した結果を別の方法で解釈する必要があります。

今回は、線形で分類できないデータを分類してみます。

円形データの生成

現実のデータではなく、scikit-learnのmake_circlesを使って、円形に散布するデータを生成します。

[Google Colaboratory]

1
2
3
4
5
6

from sklearn.datasets import make_circles

X_circle, y_circle = make_circles(random_state=42, n_samples=100, noise=0.1, factor=0.3)

plt.scatter(X_circle[:, 0], X_circle[:, 1], c=y_circle)
plt.show()

[実行結果]

上図のように、線形では分類できそうもない、円の中に円があるようなデータが生成されました。

複数のモデルを定義

複数のモデルを構築するために、それぞれのモデルを辞書型で定義します。

[Google Colaboratory]

1
2
3
4
5
6

models = {"Logistic Regression":LogisticRegression(), 
          "Linear SVM":LinearSVC(random_state=0),
          "Kernel SVM":SVC(kernel="rbf",random_state=0),
          "K Neighbors":KNeighborsClassifier(),
          "Decision Tree":DecisionTreeClassifier(max_depth=3,random_state=0),
          "Random Forest":RandomForestClassifier(max_depth=3,random_state=0)}

モデル構築・決定境界の可視化

定義した辞書内容をもとに、各モデルの構築と決定境界の可視化をまとめて行います。

[Google Colaboratory]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

import matplotlib.gridspec as gridspec
import itertools

gs = gridspec.GridSpec(2, 3)
fig = plt.figure(figsize=(12, 6))

for model_name, num in zip(models.keys(), itertools.product([0, 1, 2],repeat=2)):

  model = models[model_name].fit(X_circle,y_circle)
  
  ax = plt.subplot(gs[num[0], num[1]])
  fig = plot_decision_regions(X_circle, y_circle,clf=model)
  plt.title(model_name)

plt.tight_layout()
plt.show()

[実行結果]

それぞれのモデルの決定境界を一括で可視化できました。

上記の図から、ロジスティック回帰や線形SVMのような線形系アルゴリズムでは、今回のデータセットには全く対応できていないことが把握できます。

一方、カーネルSVM、K近傍法、ランダムフォレストでは適切に分類することができています。

アルゴリズムを選択する際には、まずデータセットの散布状況を確認し線形分離できそうかどうかを確認するのがよさそうです。

ランダムフォレストは、複数の異なる決定木を生成し、予測結果を総合的に判断するアルゴリズムです。

回帰では各決定木から得られた結果の平均を予測値としていましたが、分類では各決定木の結果の多数決で予測値を決定します。

単一の決定木と比較して、モデルの解釈性は劣るものの過学習を抑えられ、精度の向上が期待できます。

ランダムフォレストモデルの構築

ランダムフォレストの分類モデルを構築するためには、scikit-learnのRandomForestClassifierクラスを使います。

前回記事にて実行した決定木モデルの結果と比較するため、max_depthの値は3にします。

[Google Colaboratory]

1
2

from sklearn.ensemble import RandomForestClassifier
rf_cls = RandomForestClassifier(max_depth=3,random_state=0).fit(X_train, y_train)

ランダムフォレストのようなアンサンブル学習を行うアルゴリズムは、SVMや決定木に比べてハイパーパラメータのチューニングをシビアに行わなくても、ある程度高い精度が出やすいことが特徴となります。

決定境界の可視化

plot_decision_regionsメソッドを使い決定境界を可視化します。

[Google Colaboratory]

1
2

plot_decision_regions(np.array(X_train), np.array(y_train), clf=rf_cls)
plt.show()

[実行結果]

ランダムフォレストでは複数の決定木の結果をもとに分類予測を行うため、単一の決定木と比較して複雑な決定境界が引かれます。

決定木は、回帰問題だけでなく分類問題でもよく使われるアルゴリズムです。

モデルの解釈性が優れていることや、過学習に陥りやすいという特徴があります。

またハイパーパラメータの種類も決定木回帰と共通するものが多いです。

決定木モデルの構築

決定木の分類モデルを構築するためには、scikit-learnのDecisionTreeClassifierクラスを使います。

【参考】決定木の回帰モデルではDecisionTreeRegressorクラスを使いました。

[Google Colaboratory]

1
2

from sklearn.tree import DecisionTreeClassifier 
tree_cls = DecisionTreeClassifier(max_depth=3,random_state=0).fit(X_train, y_train)

モデルが複雑になるのを避けるため、決定木の層の最大深さ(max_depth)を3に指定しました。

訓練データにはスケーリング前のデータを使用しています。

決定木は単一の説明変数の大小に着目したアルゴリズムであるため、スケーリングの必要がないためです。

決定境界の可視化

plot_decision_regionsメソッドを使い決定境界を可視化します。

[Google Colaboratory]

1
2
3
4

plot_decision_regions(np.array(X_train), np.array(y_train), clf=tree_cls)
plt.xlabel("mean radius")
plt.ylabel("mean texture")
plt.show()

[実行結果]

これまで試してきたアルゴリズムとはかなり違う形の決定境界となっています。

どうしてこのような分類になったのかを確認するために、決定木の内容を確認します。

決定木の可視化

決定木を可視化します。

視覚的に分かりやすくするため、ノード内のサンプルが占めるカテゴリの割合(value)に応じて各ノードを色分けしています。

またサンプル数とvalueの値は割合で表示しています。

[Google Colaboratory]

1
2
3
4
5

from sklearn import tree

plt.figure(figsize=(20,8))
tree.plot_tree(tree_cls,feature_names=["mean radius","mean texture"],filled=True,proportion=True,fontsize=8)
plt.show()

[実行結果]

決定木の各条件を上から順に散布図に当てはめていくと、先ほど可視化したものと同じようにカクカクした決定境界となります。

このように決定木を可視化することでどのような条件でどのカテゴリに分類されるのかが説明可能になります。

K近傍法は、周辺にあるK個の訓練データがどちらに分類されているか多数決で分類するアルゴリズムです。

これまでのアルゴリズムのように計算をして傾向を導き出すのではなく、単純に訓練データを丸暗記している点が大きく異なります。

K近傍法のような学習のアプローチを怠惰学習と呼ぶこともあります。

K近傍法モデルの構築

K近傍法モデルを構築するためには、scikit-learnのKNeighborsClassifierクラスを使用します。(2行目)

引数の意味は下記の通りです。

• n_neighbors
  予測時に見る訓練データの数。
• p
  距離の指標。
  1がユークリッド距離、2がマンハッタン距離の指定となります。

[Google Colaboratory]

1
2

from sklearn.neighbors import KNeighborsClassifier
kn_cls = KNeighborsClassifier(n_neighbors=5, p=2).fit(X_train_scaled, y_train)

データセットは、これまでと同じ「乳がんの診断データ」を使用しています。

複雑な計算を行っていないため、学習プロセスは高速に完了します。

決定境界の可視化

plot_decision_regionsメソッドを使い決定境界を可視化します。

[Google Colaboratory]

1
2

plot_decision_regions(np.array(X_train_scaled), np.array(y_train), clf=kn_cls)
plt.show()

[実行結果]

K近傍法では、暗記した訓練データを予測時に参照するという特徴から、学習は高速で終わりますが、予測には時間がかかります。

また訓練データ数が多くなるほど、予測に要する時間が長くなる傾向があります。

計算コストが高くなりやすい一方で、モデルの解釈が容易でありどのようなデータセットにも比較的柔軟に対応できるという長所があります。

カーネル法は、線形分離できないデータを線形分離できる状態に変換する手法です。

カーネル法により変換されたデータに対して、線形SVMで決定境界を引いた後に元の状態に逆変換します。

こうすることにより非線形の決定境界を引くことができます。

カーネルSVMモデル 構築・可視化

カーネルSVMモデルを構築するためにはscikit-learnのSVCクラスを使用します。（2行目）

[Google Colaboratory]

1
2
3
4
5

from sklearn.svm import SVC
kernel_svm = SVC(kernel="rbf",random_state=0).fit(X_train_scaled, y_train)

plot_decision_regions(np.array(X_train_scaled), np.array(y_train), clf=kernel_svm)
plt.show()

データセットは、これまでと同じ「乳がんの診断データ」を使用し、前回記事同様plot_decision_regionsメソッドを使い決定境界を可視化します。

[実行結果]

上図のように直線ではない決定境界を引くことができました。

線形による分類よりも、非線形による分類の方が適切に境界を分けることができています。

線形SVM(サポートベクターマシン)は、ロジスティック回帰と同じように線形分離できるケースで高いパフォーマンスを発揮するアルゴリズムです。

線形SVMモデル 構築・可視化

線形SVMモデルの構築にはscikit-learnのLinearSVCクラスを使用します。（2行目）

[Google Colaboratory]

1
2
3
4
5

from sklearn.svm import LinearSVC
linear_svm = LinearSVC(random_state=0).fit(X_train_scaled, y_train)

plot_decision_regions(np.array(X_train_scaled), np.array(y_train), clf=linear_svm)
plt.show()

データセットは、これまでと同じ「乳がんの診断データ」を使用し、前回記事同様plot_decision_regionsメソッドを使い決定境界を可視化します。

[実行結果]

ロジスティック回帰とよく似た結果となりました。

ロジスティック回帰と線形SVMの違いはデータの外れ値の影響を受けにくい点です。

ロジスティック回帰は確率論に基づいたアルゴリズムでしたが、線形SVMはマージンの最大化に着目したアルゴリズムとなります。

決定境界に最も近いデータ点のことをサポートベクターと呼びますが、線形SVMはそのサポートベクターとの距離（マージン）が最大になる決定境界を引くアルゴリズムです。

なお、SVMは非線形の分類を行うこともできます。

次回は、非線形SVMでの分類を行ってみます。

データの分類予測の基準となる境界線のことを決定境界と言います。

前回構築したロジスティック回帰モデルではどのような決定境界が引かれているのかを可視化してみます。

決定境界を可視化

決定境界の可視化にはmlxtendというライブラリを使用します。

データとモデルを渡すだけで決定境界を可視化してくれるとても便利なライブラリです。

[Google Colaboratory]

1
2
3
4
5

import numpy as np
from mlxtend.plotting import plot_decision_regions

plot_decision_regions(np.array(X_train_scaled), np.array(y_train), clf=log_reg)
plt.show()

plot_decision_regionsメソッドの引数は下記の通りです。（4行目）

• 第１引数
  スケーリングした訓練データの説明変数
• 第２引数
  訓練データの目的変数
• 第３引数(clf)
  構築したロジスティック回帰モデル

[実行結果]

構築したロジスティック回帰モデルでは、上図のような直線で決定境界が引かれています。

直線という制約があるので、決定境界周辺では正しく分類でいていないデータが多いようです。

ロジスティック回帰はデータを直線で分類（線形分離）できるケースに適したアルゴリズムです。

また、単純かつ計算コストが低いという特徴もあります。

ロジスティック回帰は、二値分類でよく使われる手法で、回帰分析のプロセスを経て分類予測を行います。

ロジスティック回帰では、重み付けされた説明変数の和から、一方に分類される確率を算出し閾値（50%）を上回るかどうかで最終的な分類を決定します。

良性に分類される確率が40%であれば悪性に分類されることになります。

ロジスティック回帰モデルの構築

ロジスティック回帰モデルを構築するには、scikit-learnのLogisticRegressionクラスを使用します。

[Google Colaboratory]

1
2
3

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(random_state=0).fit(X_train_scaled, y_train)

予測結果を出力します。

[Google Colaboratory]

1
2
3
4
5

y_train_pred = log_reg.predict(X_train_scaled)
y_test_pred = log_reg.predict(X_test_scaled)

print(y_train_pred[:5])
print(y_test_pred[:5])

[実行結果]

ラベルデータである0, 1がきちんと出力されていることが分かります。

可視化（訓練データ）

訓練データの予測結果を可視化します。

[Google Colaboratory]

1
2
3
4
5

plt.scatter(X_train["mean radius"],X_train["mean texture"], c=y_train_pred)
plt.title("Pred_Train") 
plt.xlabel("mean radius")
plt.ylabel("mean texture")
plt.show()

[実行結果]

可視化（テストデータ）

テストデータの予測結果を可視化します。

[Google Colaboratory]

1
2
3
4
5

plt.scatter(X_test["mean radius"],X_test["mean texture"], c=y_test_pred)
plt.title("Pred_Test") 
plt.xlabel("mean radius")
plt.ylabel("mean texture")
plt.show()

[実行結果]

ある直線を境にきれいにデータが２分割されています。

次回は、この直線に焦点を当てて可視化を行います。

モデル構築の下準備として、データの前処理を行います。

目的変数と説明変数に分割

まずデータを説明変数 X と目的変数 y に分けます。

[Google Colaboratory]

1
2
3
4
5

X= tg_df[["mean radius","mean texture"]]
y = tg_df["y"]

display(X.head())
display(y.head())

[実行結果]

訓練データとテストデータに分割

次に、データを訓練データ(70%)とテストデータ(30%)に分割します。

[Google Colaboratory]

1
2
3
4
5
6
7
8

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.3,random_state=0)

print(len(X_train))
display(X_train.head())
print(len(X_test))
display(X_test.head())

[実行結果]

スケーリング

最後に、データの尺度をそろえるためスケーリングを行います。

[Google Colaboratory]

1
2
3
4
5
6
7
8

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

print(X_train_scaled[:3])
print(X_test_scaled[:3])

[実行結果]

次回は、ロジスティック回帰モデルの構築を行います。