線形SVMモデル （決定境界）

線形SVM(サポートベクターマシン)は、ロジスティック回帰と同じように線形分離できるケースで高いパフォーマンスを発揮するアルゴリズムです。

線形SVMモデル 構築・可視化

線形SVMモデルの構築にはscikit-learnのLinearSVCクラスを使用します。（2行目）

[Google Colaboratory]

from sklearn.svm import LinearSVC
linear_svm = LinearSVC(random_state=0).fit(X_train_scaled, y_train)

plot_decision_regions(np.array(X_train_scaled), np.array(y_train), clf=linear_svm)
plt.show()

データセットは、これまでと同じ「乳がんの診断データ」を使用し、前回記事同様plot_decision_regionsメソッドを使い決定境界を可視化します。

[実行結果]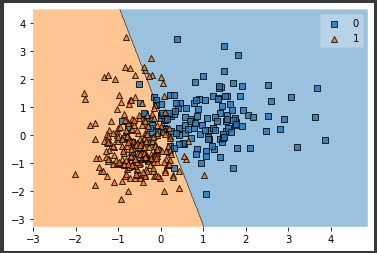

ロジスティック回帰とよく似た結果となりました。

ロジスティック回帰と線形SVMの違いはデータの外れ値の影響を受けにくい点です。

ロジスティック回帰は確率論に基づいたアルゴリズムでしたが、線形SVMはマージンの最大化に着目したアルゴリズムとなります。

決定境界に最も近いデータ点のことをサポートベクターと呼びますが、線形SVMはそのサポートベクターとの距離（マージン）が最大になる決定境界を引くアルゴリズムです。

なお、SVMは非線形の分類を行うこともできます。

次回は、非線形SVMでの分類を行ってみます。