フォッカー-プランク方程式

フォッカー-プランク方程式は、確率過程の時間発展を記述する偏微分方程式です。

例えば、ブラウン運動などの確率過程の確率密度関数の時間変化を記述します。

1次元のフォッカー-プランク方程式は以下のように表されます。

∂P(x,t)/∂t=−∂/∂x[D(1)(x,t)P(x,t)]+(1/2)∂2/∂x2[D(2)(x,t)P(x,t)]

ここで、P(x,t)は確率密度関数、D(1)(x,t)は漂流係数、D(2)(x,t)は拡散係数です。

この方程式をPythonで解くには、数値計算が必要になります。
ここでは、有限差分法を使って近似的に解きます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 定数
D1 = 0.1  # 漂流係数
D2 = 0.01  # 拡散係数
X_MAX = 10.0  # x範囲
T_MAX = 10.0  # 時間範囲
N_X = 100  # x方向の分割数
N_T = 1000  # 時間ステップ数

# 配列の初期化
dx = X_MAX / (N_X - 1)
dt = T_MAX / (N_T - 1)
x = np.linspace(0, X_MAX, N_X)
t = np.linspace(0, T_MAX, N_T)
P = np.zeros((N_T, N_X))

# 初期条件
P[0] = np.exp(-(x - 3)**2 / 0.5)  # ガウス分布

# フォッカー-プランク方程式の解法
for i in range(N_T - 1):
    for j in range(1, N_X - 1):
        P[i+1, j] = P[i, j] \
                    - dt * (D1 * (P[i, j+1] - P[i, j-1]) / (2 * dx)) \
                    + (D2 * dt / (2 * dx**2)) * (P[i, j+1] - 2 * P[i, j] + P[i, j-1])
    P[i+1, 0] = P[i+1, 1]  # 端の条件
    P[i+1, -1] = P[i+1, -2]  # 端の条件

# 結果のプロット
fig, ax = plt.subplots(figsize=(8, 6))
for i in range(0, N_T, 100):
    ax.plot(x, P[i], label=f't = {t[i]:.2f}')
ax.set_xlabel('x')
ax.set_ylabel('P(x,t)')
ax.set_title('Fokker-Planck Equation')
ax.legend()
plt.show()

このコードでは、フォッカー-プランク方程式を有限差分法で近似的に解いています。
初期条件としてガウス分布を与え、時間発展させています。

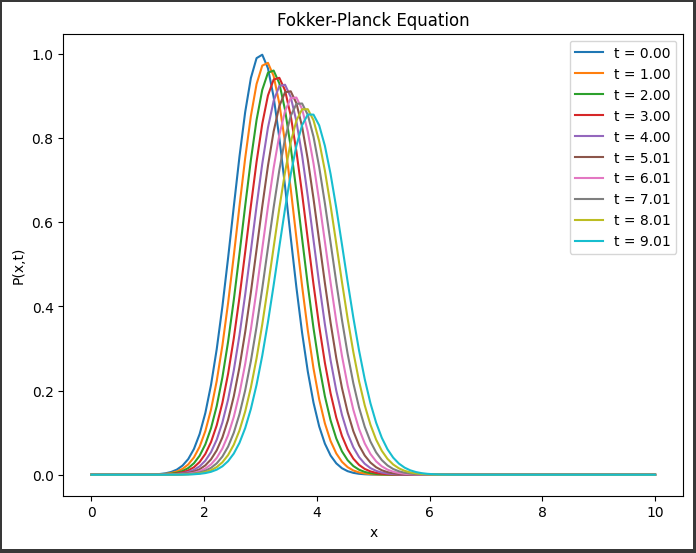
出力される図は、確率密度関数P(x,t)の時間変化を示しています。
時間が経つにつれて、分布が拡散していく様子が確認できます。

[実行結果]

ソースコード解説

ここでは、フォッカー-プランク方程式の数値解を計算し、その結果を可視化するPythonコードについて説明します。

1. ライブラリのインポートと設定

1
2
3

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

NumPyとMatplotlibライブラリをインポートし、Matplotlibのインラインモードを有効にしています。

2. 定数の設定

1
2
3
4
5
6

D1 = 0.1  # 漂流係数
D2 = 0.01  # 拡散係数
X_MAX = 10.0  # x範囲
T_MAX = 10.0  # 時間範囲
N_X = 100  # x方向の分割数
N_T = 1000  # 時間ステップ数

フォッカー-プランク方程式の係数(D1,D2)、計算範囲(XMAX,TMAX)、空間と時間の分割数(NX,NT)を設定しています。

3. 配列の初期化

1
2
3
4
5

dx = X_MAX / (N_X - 1)
dt = T_MAX / (N_T - 1)
x = np.linspace(0, X_MAX, N_X)
t = np.linspace(0, T_MAX, N_T)
P = np.zeros((N_T, N_X))

空間と時間の刻み幅(dx,dt)、座標と時間の配列(x,t)、確率密度関数の配列P(NTxNX)を初期化しています。

4. 初期条件の設定

1

P[0] = np.exp(-(x - 3)**2 / 0.5)  # ガウス分布

初期の確率密度関数にガウス分布(平均値3、分散0.5)を設定しています。

5. フォッカー-プランク方程式の解法

1
2
3
4
5
6
7

for i in range(N_T - 1):
    for j in range(1, N_X - 1):
        P[i+1, j] = P[i, j] \
                    - dt * (D1 * (P[i, j+1] - P[i, j-1]) / (2 * dx)) \
                    + (D2 * dt / (2 * dx**2)) * (P[i, j+1] - 2 * P[i, j] + P[i, j-1])
    P[i+1, 0] = P[i+1, 1]  # 端の条件
    P[i+1, -1] = P[i+1, -2]  # 端の条件

フォッカー-プランク方程式を有限差分法で近似的に解いています。

時間ループとx方向のループを使って、各時間ステップと空間格子点における確率密度関数の値を計算しています。
また、端の条件も設定しています。

6. 結果のプロット

1
2
3
4
5
6
7
8

fig, ax = plt.subplots(figsize=(8, 6))
for i in range(0, N_T, 100):
    ax.plot(x, P[i], label=f't = {t[i]:.2f}')
ax.set_xlabel('x')
ax.set_ylabel('P(x,t)') 
ax.set_title('Fokker-Planck Equation')
ax.legend()
plt.show()

最後に、計算結果をプロットしています。
時間ステップごとに確率密度関数P(x,t)をプロットし、各曲線に対応する時刻tを凡例に表示しています。
また、軸ラベルとタイトルを設定し、グラフを表示しています。

このコードでは、フォッカー-プランク方程式の数値解を計算し、確率密度関数の時間発展を可視化しています。
初期条件にガウス分布を与え、時間の経過とともに確率密度がどのように拡散していくかを示しています。

結果解説

[実行結果]

出力されるグラフは、確率密度関数 P(x,t)の時間発展を示しています。

• 横軸はxで、確率変数の値を表します。
• 縦軸はP(x,t)で、その時刻tにおける確率密度を表します。

グラフには複数の曲線が描かれています。
それぞれの曲線は異なる時刻tにおける確率密度関数P(x,t)を表しています。

• 初期条件(t=0)の曲線は、平均値が3、分散が0.5のガウス分布になっています。
• 時間が経つにつれ、曲線が広がっていく様子が見て取れます。
  これは確率密度関数が拡散していることを表しています。
• 端(x=0およびx=XMAX)の条件を満たすため、曲線の両端は0に近づくように調整されています。

凡例には、各曲線に対応する時刻tが表示されています。
例えば、最初の曲線はt=0.00、次の曲線はt=1.00というように時間が経過しています。

このグラフから、次のような情報が読み取れます:

1. 初期の確率分布の形状
2. 時間の経過とともに確率分布がどのように変化するか
3. 確率密度がどのように拡散し、平らになっていくか
4. 端の条件がどのように満たされているか

フォッカー-プランク方程式は、このように確率過程の時間発展を記述する役割があり、このグラフはその数値解の可視化結果になっています。

ガウス-ボナールの微分方程式

ガウス-ボナールの微分方程式は、曲面の局所的な幾何学的性質を記述する重要な式です。

この式は以下のように表されます:

k=KdA

• k は曲面上の任意の閉曲線の総曲率です。
• K は曲面のガウス曲率です。
  ガウス曲率は、曲面上の点における内在的な曲がり具合を表します。
• dA は閉曲線に囲まれた小さな領域の面積です。

つまり、ガウス-ボナールの式は、閉曲線の総曲率が、その曲線に囲まれた領域のガウス曲率に比例することを示しています。

この式は、位相幾何学の分野で非常に重要です。
特に、コンパクト(閉じた有界)な曲面のトポロジー(位相的な形状)は、その曲面のガウス曲率に関係しているためです。

具体的な応用例としては、一般相対性理論におけるアインシュタインの方程式の導出や、相対論的な宇宙モデルの研究などがあります。
また、コンピューターグラフィックスにおける曲面モデリングにも使われています。

このように、ガウス-ボナールの式は、曲面の局所的な性質とグローバルな性質を関連付ける重要な式なのです。

ソースコード

Pythonを使用してガウス-ボナール方程式を解き、その解をグラフ化する例を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt

# ガウス-ボナールの微分方程式
def gauss_bonnet(u, v):
    k = 1  # カーブの曲率
    return k * np.sqrt(1 + u**2 + v**2)

# パラメータの範囲
u = np.linspace(-2, 2, 50)
v = np.linspace(-2, 2, 50)
U, V = np.meshgrid(u, v)

# 数値解の計算
Z = gauss_bonnet(U, V)

# グラフの描画
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(U, V, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('u')
ax.set_ylabel('v')
ax.set_zlabel('z')
ax.set_title('Gauss-Bonnet Equation')
plt.show()

このコードは以下の手順で動作します。

1. NumPyとMatplotlibをインポートし、3D描画用のモジュールをインポートします。
2. ガウス-ボナールの微分方程式を定義した関数gauss_bonnetを作成します。
   この関数は、曲率kと変数u、vを引数にとり、微分方程式の解を返します。
3. パラメータuとvの範囲をnp.linspace関数を使って設定します。
4. np.meshgrid関数を使って、uとvの全ての組み合わせを計算します。
5. gauss_bonnet関数を使って、微分方程式の数値解Zを計算します。
6. Matplotlibを使って3D図を作成し、plot_surface関数で数値解の曲面を描画します。
7. 軸ラベルとタイトルを設定します。
8. plt.show()で、グラフを表示します。

このコードを実行すると、ガウス-ボナールの微分方程式の数値解が3D曲面として描画されます。
変数uとvの値によって、曲面の形状が変化することがわかります。

[実行結果]

注意点として、このコードではガウス-ボナールの微分方程式の特定の解のみを可視化しています。
実際の微分方程式の解は、初期条件や境界条件によって異なります。
より一般的な解を可視化するには、微分方程式の数値解法を適用する必要があります。

結果解説

[実行結果]

この3D曲面グラフには、いくつかの重要な特徴があります。

詳しく説明しましょう。

1. 曲面の形状

• この曲面は、ガウス-ボナールの微分方程式の数値解を表しています。
• 曲面の形状は、変数uとvの値によって変化します。
• 中心付近では平らな形状ですが、外側に向かうにつれて曲率が大きくなり、山のような形状になります。

2. 曲面の色

• 曲面の色は、カラーマップviridisを使って割り当てられています。
• 青から緑、黄色、オレンジ、赤と変化し、高さ(zの値)が大きいほど赤に近い色になります。
• 色の変化によって、曲面の高低差が視覚的に分かりやすくなります。

3. 軸とラベル

• x軸は変数u、y軸は変数v、z軸は微分方程式の解zを表しています。
• 各軸にはラベル(‘u’、’v’、’z’)が付けられています。

4. タイトル

• グラフのタイトルは’Gauss-Bonnet Equation’となっています。

5. プロットの詳細

• rstride=1, cstride=1のオプションにより、曲面のメッシュ解像度が最大になっています。
• つまり、すべてのデータ点が曲面にプロットされ、滑らかな表面が得られます。

このように、生成されるグラフは、ガウス-ボナールの微分方程式の数値解の3D表現を視覚化したものです。

変数の値によって曲面の形状が変化し、色分けによって高低差が分かりやすくなっています。

軸ラベルとタイトルも付加されているため、グラフの解釈がしやすくなっています。

ステファン・ボルツマンの法則

ステファン・ボルツマンの法則は、物体が放射するエネルギーの量を温度と関連付ける物理法則です。

この法則によれば、物体が放射する熱エネルギーの放射束は、その温度の4乗に比例します。

具体的には、放射束 （W/m2）は絶対温度 （K）の4乗に比例します。

つまり、物体が高温になるほど、放射するエネルギーの量が急速に増加します。

この法則は、宇宙や星、地球の大気など、さまざまな物体の放射特性を理解するのに役立ちます。

ソースコード

ステファン・ボルツマンの法則は、放射されるエネルギーの強度（放射束）が、絶対温度の4乗に比例することを述べます。

数式的には、以下のように表されます。

E=σ⋅T4

ここで、(E)は放射束、(σ)はステファン・ボルツマン定数（(σ=5.67×10−8)W/m(2)/K(4))、(T)は絶対温度です。

以下のPythonコードでは、異なる温度における放射束を計算し、それをグラフ化しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

import numpy as np
import matplotlib.pyplot as plt

# ステファン・ボルツマン定数
sigma = 5.67e-8  # W/m^2/K^4

# 絶対温度の範囲を定義
T_values = np.linspace(100, 1000, 100)  # 100 K から 1000 K まで

# 放射束を計算
radiative_flux = sigma * T_values**4

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(T_values, radiative_flux)
plt.title('Stefan-Boltzmann Law')
plt.xlabel('Temperature (K)')
plt.ylabel('Radiative Flux (W/m^2)')
plt.grid(True)
plt.show()

このコードでは、100Kから1000Kの範囲で絶対温度を変化させ、それぞれの温度における放射束を計算し、それをグラフにプロットしています。

[実行結果]

ソースコード解説

以下に、ソースコードの詳細を示します。

1. import numpy as npとimport matplotlib.pyplot as pltは、それぞれNumPyおよびMatplotlibパッケージをインポートします。
   これらのパッケージは数値計算やグラフ描画に使用されます。

2. sigma = 5.67e-8は、ステファン・ボルツマン定数を定義しています。
   この定数は、放射束と温度の関係を示す物理定数です。

3. T_values = np.linspace(100, 1000, 100)は、100Kから1000Kまでの範囲で100個の等間隔の温度値を生成します。
   これは絶対温度の範囲を指定しています。

4. radiative_flux = sigma * T_values**4は、ステファン・ボルツマンの法則に基づいて、各温度における放射束を計算します。
   放射束は温度の4乗に比例するので、この式を使用して放射束を計算しています。

5. plt.figure(figsize=(8, 6))は、グラフのサイズを設定しています。

6. plt.plot(T_values, radiative_flux)は、計算された放射束を温度に対してプロットしています。
   温度が増加するにつれて放射束がどのように変化するかを示しています。

7. plt.title('Stefan-Boltzmann Law')、plt.xlabel('Temperature (K)')、plt.ylabel('Radiative Flux (W/m^2)')は、それぞれグラフのタイトルと軸ラベルを設定しています。

8. plt.grid(True)は、グリッド線を表示するように設定しています。

9. plt.show()は、グラフを表示します。

これにより、ステファン・ボルツマンの法則に基づいて計算された放射束の温度依存性が視覚化され、温度が上昇するにつれて放射束がどのように増加するかがわかります。

グラフ解説

[実行結果]

このグラフは、ステファン・ボルツマンの法則に基づいて計算された放射束を表しています。
横軸は温度（絶対温度、K）を示し、縦軸は放射束 （W/m2）を表します。
放射束は温度の4乗に比例するため、温度が上昇するにつれて急速に増加します。

グラフを見ると、温度が低いとき（100K付近）は放射束が非常に低いことがわかります。
しかし、温度が上昇するにつれて放射束が急速に増加し、高温領域では非常に大きな値を示します。

これは、高温の物体がより多くのエネルギーを放射するためです。
ステファン・ボルツマンの法則は、このような温度と放射束の関係を定量化しています。

ベッセルの微分方程式

ベッセルの微分方程式は、円筒対称な問題や振動問題などさまざまな分野で現れる微分方程式です。

主に、円筒座標系や球面座標系における偏微分方程式の解析解を求める際に用いられます。

ベッセルの微分方程式は以下の形式で表されます：

x2y″(x)+xy′(x)+(x2−ν2)y(x)=0

ここで、(y(x))は未知関数、(ν)は定数です。
この方程式は通常、変数分離法やフロベニウス法などの手法を用いて解かれます。

ベッセルの微分方程式の解は、第1種ベッセル関数 (Jν(x))および第2種ベッセル関数 (Yν(x))と呼ばれる関数で表されます。

これらの関数は、数学的な性質や物理的な問題における様々な問題に利用されます。

Pythonコード

ベッセルの微分方程式を解くためには、SciPyのscipy.specialモジュールに含まれるjv関数を使用します。
この関数は、第1種ベッセル関数を計算するために使われます。

以下は、ベッセルの微分方程式をPythonで解いてグラフ化するコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt
from scipy.special import jv

# 解析的解を計算する関数
def solve_bessel_equation(x_values, order):
    return jv(order, x_values)

# x軸の値を定義
x_values = np.linspace(0, 20, 400)  # 0から20までの範囲を400点で分割

# ベッセルの微分方程式の解を計算
order = 0  # ベッセル関数の次数
bessel_solution = solve_bessel_equation(x_values, order)

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(x_values, bessel_solution, label=f'Order {order}')
plt.title('Solution of Bessel Equation')
plt.xlabel('x')
plt.ylabel('Solution')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、scipy.special.jv関数を使用してベッセルの微分方程式の解を計算し、それをグラフ化しています。

x_valuesはx軸の値を指定し、orderはベッセル関数の次数を示します。

[実行結果]

ソースコード解説

このプログラムは、ベッセルの微分方程式の解析的解を計算し、グラフ化するものです。

1. NumPyおよびMatplotlibのインポート:

• import numpy as np：NumPyライブラリをnpとしてインポートします。
• import matplotlib.pyplot as plt：Matplotlibのpyplotモジュールをpltとしてインポートします。

2. Scipyの特殊関数モジュールからベッセル関数をインポート:

• from scipy.special import jv：Scipyライブラリのspecialモジュールからベッセル関数をインポートします。

3. ベッセルの微分方程式の解析的解を計算する関数:

• solve_bessel_equation(x_values, order)：与えられた次数（order）のベッセル関数の値を、与えられたxの値に対して計算します。

4. x軸の値を定義:

• x_values = np.linspace(0, 20, 400)：0から20の範囲を等間隔で400点に分割した値をx_valuesに格納します。

5. ベッセルの微分方程式の解を計算:

• order = 0：計算するベッセル関数の次数を設定します（ここでは0次のベッセル関数を計算しています）。
• bessel_solution = solve_bessel_equation(x_values, order)：定義した関数を用いて、ベッセルの微分方程式の解析的解を計算します。

6. グラフのプロット:

• plt.figure(figsize=(8, 6))：新しい図を作成し、図のサイズを指定します。
• plt.plot(x_values, bessel_solution, label=f'Order {order}')：x_valuesに対応するベッセル関数の値をプロットします。
  ラベルには計算したベッセル関数の次数が表示されます。
• plt.title('Solution of Bessel Equation')：図のタイトルを設定します。
• plt.xlabel('x')：x軸のラベルを設定します。
• plt.ylabel('Solution')：y軸のラベルを設定します。
• plt.legend()：凡例を表示します。
• plt.grid(True)：グリッド線を表示します。
• plt.show()：グラフを表示します。

結果解説

[実行結果]

上記のグラフは、ベッセルの微分方程式の解である第1種ベッセル関数 (J0(x))を示しています。

横軸は(x)を表し、縦軸は対応するベッセル関数の値を表します。
このグラフは、0から20の範囲でベッセル関数を計算し、それをプロットしています。

ベッセル関数は、振動する性質を持ち、(x)の増加に伴い周期的に振動します。
また、(x)の値が小さいときには振動の幅が大きく、(x)の値が大きいときには振動の幅が小さくなる傾向があります。

このグラフは、ベッセルの微分方程式の解である(J0(x))の振る舞いを視覚的に示しています。

トリッツ行列方程式

トリッツ行列方程式は、特定の形式の行列に対する連立方程式です。
この行列は対角成分とその両隣の要素だけが非ゼロである特別な形をしています。
典型的には、対角線上の要素はすべて同じで、その隣の要素は同じ定数倍の値を持ちます。

トリッツ行列方程式は、このような特殊な形を持つ行列に対する連立方程式を解くことを目的としています。
この方程式は、科学や工学のさまざまな分野で利用されます。
例えば、熱伝導や波動方程式などの数値解法において、離散化された空間領域での連立方程式を解く際にトリッツ行列方程式が現れることがあります。

トリッツ行列方程式の解法は、特定のアルゴリズムや数値解法を使用して行われます。
一般に、行列の次元が大きくなるにつれて、解法の計算コストが増加する傾向があります。

ソースコード

トリッツ行列方程式をPythonで解いてグラフ化するために、NumPyとMatplotlibを使用します。
以下は、トリッツ行列方程式を解くPythonコードの例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

import numpy as np
import matplotlib.pyplot as plt

# トリッツ行列方程式の解析的解を計算する関数
def tridiagonal_matrix_eq(n):
    main_diag = 2 * np.ones(n)  # 対角要素
    sub_diag = -1 * np.ones(n-1)  # 下部対角要素

    # 係数行列を作成
    A = np.diag(main_diag) + np.diag(sub_diag, k=-1) + np.diag(sub_diag, k=1)

    # 右辺ベクトルを定義
    b = np.ones(n)

    # 係数行列を連立方程式を解く
    x = np.linalg.solve(A, b)
    return x

# グラフをプロット
n_values = np.arange(2, 11)  # 行列のサイズを2から10まで変化させる
plt.figure(figsize=(8, 6))
for n in n_values:
    x = tridiagonal_matrix_eq(n)
    plt.plot(range(1, n+1), x, label=f'n={n}')

plt.xlabel('Index')
plt.ylabel('Solution')
plt.title('Solution of Tridiagonal Matrix Equation')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、トリッツ行列方程式の解析的解を計算する関数 tridiagonal_matrix_eq を定義しています。

np.linalg.solve を使用して、各行列サイズに対する方程式の解を計算し、それらをグラフにプロットしています。

[実行結果]

ソースコード解説

このソースコードは、トリッツ行列方程式を解くPythonプログラムです。
以下は、コードの詳細な説明です。

1. tridiagonal_matrix_eq 関数:

• この関数は、与えられた次元のトリッツ行列方程式の解析的解を計算します。
• n を引数として受け取り、行列の次元として使用します。
• main_diag は、対角要素の値を示す1次元NumPy配列です。
  対角要素はすべて2で、n の長さを持ちます。
• sub_diag は、下部対角要素の値を示す1次元NumPy配列です。
  下部対角要素はすべて-1で、長さは n-1 です。
• 行列 A を作成します。
  これは、main_diag と sub_diag を使用して、トリッツ行列の係数行列を表します。
• 右辺ベクトル b は、要素がすべて1で、長さがn の1次元NumPy配列です。
• np.linalg.solve() 関数を使用して、係数行列 A と右辺ベクトル b から方程式を解きます。

2. グラフのプロット:

• n_values は、行列の次元を2から10まで変化させるための配列です。
• plt.figure() 関数で新しいプロットを作成し、図のサイズを指定します。
• for ループを使用して、各 n について tridiagonal_matrix_eq() を呼び出し、解を計算します。
• plt.plot() 関数を使用して、解のグラフをプロットします。
  各解は、インデックス番号に対応する x 軸の値に対してプロットされます。
• plt.xlabel()、plt.ylabel()、plt.title() 関数を使用して、軸ラベルとタイトルを設定します。
• plt.legend() 関数を使用して、各解に対する凡例を追加します。
• plt.grid(True) でグリッドを表示し、plt.show() でグラフを表示します。

このコードは、トリッツ行列方程式の解を計算し、さまざまな行列の次元に対する解をグラフ化しています。

行列の次元が増加するにつれて、解がどのように振る舞うかを視覚的に理解するのに役立ちます。

結果解説

[実行結果]

このグラフは、トリッツ行列方程式の解を示しています。
トリッツ行列方程式は、対角成分とその両隣の要素だけが非ゼロである特別な行列に対する連立方程式です。

横軸は行列の次元を表し、縦軸は方程式の解の値を示しています。
各曲線は、行列の次元が異なる場合の解を表しています。
次元が大きくなるにつれて、方程式の解がどのように振る舞うかを観察できます。

このグラフを見ると、行列の次元が増加するにつれて、解の振る舞いがどのように変化するかがわかります。
特に、次元が増えると、解の値が収束する傾向があることが観察されるかもしれません。
これは、行列の次元が増加するにつれて、対角成分に対する非ゼロの要素の影響が強まるためです。

このグラフは、トリッツ行列方程式の理解を深めるのに役立ちます。
行列の次元が増加すると、方程式の解がどのように振る舞うかを視覚的に理解するのに役立ちます。

トロイダル座標系

トロイダル座標系は、3次元空間の特殊な曲面を記述するための座標系です。

その主な特徴は以下の通りです。

1. 渦巻き状の形状をしています。
   つまり、円柱状の中空の管が渦を巻いているような形状をしています。

2. 3つの座標変数 (u,v,r)で表されます。

   • u: 円周方向の角度(0から2πまで)
   • v: 渦巻き方向の角度(0から2πまで)
   • r: 渦巻き半径

3. 中心軸から一定の距離rにある円環状の曲線が、v角度分ずつ回転しながら螺旋状に巻きついた形をしています。

4. 電磁気学や流体力学などで、渦巻き状の磁場やフロー場を記述するのに使われます。

5. 座標変数(u,v,r)から直交座標(x,y,z)への変換式が定義されています。

6. トロイダル座標系はトーラス(ドーナツ型)の形状の物体を自然に記述できる座標系です。

トロイダル座標系は渦巻き状の曲面や中空の管状の物体の形状を簡潔に表現するのに適した特殊な曲線座標系なのです。

電磁気学や流体力学分野で重要な役割を果たしています。

トロイダル座標系をPythonで可視化するコードを書きましょう。

トロイダル座標系は、円筒座標系と球座標系を組み合わせた座標系で、渦巻き状の曲面を表すのに便利です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# トロイダル座標系のパラメータ範囲
c = 2  # トロイダル半径
a = 1  # 渦巻き半径
u_range = np.linspace(0, 2 * np.pi, 100)
v_range = np.linspace(0, 2 * np.pi, 100)

# トロイダル座標系の変換式
U, V = np.meshgrid(u_range, v_range)
X = (c + a * np.cos(V)) * np.cos(U)
Y = (c + a * np.cos(V)) * np.sin(U)
Z = a * np.sin(V)

# 3D プロットの設定
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=5, cstride=5, cmap='viridis', edgecolor='none')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Toroidal Coordinate System')

plt.show()

このコードでは、以下の手順で作業を行っています。

1. numpy と matplotlib をインポートし、3D プロットに必要な Axes3D も読み込みます。
2. トロイダル座標系のパラメータ c (トロイダル半径)、a (渦巻き半径)、および u、v の範囲を設定します。
3. np.meshgrid を使って、u、v の値の組み合わせを生成します。
4. トロイダル座標系の変換式を使って、各 (u, v) の組み合わせに対応する (x, y, z) の値を計算します。
5. matplotlib の plot_surface 関数を使って、計算した (x, y, z) の値から3D 曲面をプロットします。
6. 軸ラベルとタイトルを設定します。
7. plt.show() で最終的なプロットを表示します。

実行すると、次のようなトロイダル座標系の3D プロットが表示されるはずです。

[実行結果]

このプロットでは、トロイダル半径 c = 2、渦巻き半径 a = 1 の値を使用しています。

パラメータ c と a の値を変更すれば、異なる形状のトロイダルを描くことができます。

結果解説

[実行結果]

このグラフは、トロイダル座標系を3次元空間上に可視化したものです。
トロイダル座標系は、渦巻き状の曲面を表すのに適した座標系です。

グラフ上に表示されている曲面は、次の特徴を持っています:

1. 全体的な形状は、ドーナツ状のトーラス(環状)になっています。
   つまり、中心に空洞を持つ管状の構造をしています。

2. 曲面は渦を巻いた形状をしており、螺旋状に巻きついています。
   この螺旋の巻き具合は、トロイダル座標のvの値によって決まります。

3. 曲面の半径は一定ではありません。
   曲面の内側半径と外側半径が異なり、これがトロイダル座標のrの値に対応します。
   内側半径をトロイダル半径、外側半径を渦巻き半径と呼びます。

4. 曲面は滑らかに連続しており、自己交差することはありません。

5. 曲面の色は、viridisというカラーマップを使って割り当てられています。
   色の濃淡は、曲面の高さ(z座標値)を表しています。

6. 軸は直交するx、y、z座標で構成され、それぞれにラベルが付けられています。

このようにグラフは、トロイダル座標系の本質的な性質である渦巻き状の管状構造をリアルに可視化しています。

電磁気学や流体力学の分野で重要な役割を果たすこのような特異な曲面を、直感的に理解することができます。

ボーアの周期律

ボーアの周期律は、ボーアの原子模型に基づいて、原子の電子配置と元素の性質の周期的変化を説明する法則です。

主な内容は以下の通りです。

1. 電子は特定の軌道上を回っており、その軌道半径と運動エネルギーは主量子数nによって決まる。

2. 電子は各軌道に2n2個まで収容できる。
   n=1のK殻には2電子、n=2のL殻には8電子が入る。

3. 原子内の電子は最小のエネルギー準位から順に殻や軌道に入っていく。

4. 同じ主量子数の軌道では、エネルギー準位が低い順にs, p, d, f と入っていく。

5. 原子番号が増えるにつれ、電子配置が規則的に変化する。
   同じ電子配置を持つ元素は、化学的性質が似通っている。

6. 各周期では、アルカリ金属からハロゲンまで電子配置が変化し、性質も周期的に変化する。

7. 同じ族の元素は外側電子の数が同じなので、化学的性質が似ている。

このように、ボーアの周期律は電子配置に基づいて元素の性質を周期的に整理し、周期表の作成につながりました。

しかし完全ではなく、後にさらに発展した量子力学的な考え方に置き換えられています。

ソースコード

ボーアの原子模型に基づく原子のエネルギー準位は、次の式で与えられます：

En=−k⋅Z2⋅RHn2

ここで、(En)は第(n)準位のエネルギー、(k)はクーロン定数、(Z)は原子番号、(RH)はリュードベリ定数、(n)は主量子数です。

Pythonを使用してこの式を解き、結果をグラフ化する例を以下に示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt

def bohr_energy(n, Z=1):
    k = 8.9875517923e9  # クーロン定数 [N m^2 / C^2]
    R_H = 2.1798741e-18  # リュードベリ定数 [J]
    return -(k * Z**2 * R_H) / n**2

# 原子番号
Z = 1  # 水素原子の場合

# 主量子数の範囲を定義
n_values = np.arange(1, 11)

# エネルギー準位を計算
energy_levels = [bohr_energy(n, Z) for n in n_values]

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(n_values, energy_levels, marker='o', linestyle='-')
plt.title('Bohr Model Energy Levels')
plt.xlabel('Principal Quantum Number (n)')
plt.ylabel('Energy (J)')
plt.grid(True)
plt.show()

このコードでは、主量子数(n) の値に対するエネルギー準位を計算し、それをグラフ化しています。

[実行結果]

ソースコード解説

ソースコードの各部分を説明します。

1. NumPyとMatplotlibのインポート:

1
2

import numpy as np
import matplotlib.pyplot as plt

• NumPyはPythonで数値計算を行うためのライブラリです。
• MatplotlibはPythonでグラフ描画を行うためのライブラリです。
  このスクリプトでは、Matplotlibのpyplotモジュールを使用しています。

2. ボーアのエネルギー計算関数:

1
2
3
4

def bohr_energy(n, Z=1):
   k = 8.9875517923e9  # クーロン定数 [N m^2 / C^2]
   R_H = 2.1798741e-18  # リュードベリ定数 [J]
   return -(k * Z**2 * R_H) / n**2

• bohr_energy 関数は、ボーアの原子模型に基づいて与えられた主量子数(n)に対する原子のエネルギー準位を計算します。
  デフォルトでは水素原子の場合を考慮しており、原子番号(Z)が1となっています。

3. 原子番号の設定:

1

Z = 1  # 水素原子の場合

• Z は原子の原子番号を表し、ここでは水素原子の場合を考慮しています。

4. 主量子数の範囲の定義:

1

n_values = np.arange(1, 11)

• np.arange 関数を使って、主量子数(n)の値を1から10までの範囲で定義しています。

5. エネルギー準位の計算:

1

energy_levels = [bohr_energy(n, Z) for n in n_values]

• bohr_energy 関数を使って、与えられた主量子数(n)に対するエネルギー準位を計算し、リスト energy_levels に格納しています。

6. グラフのプロット:

1
2
3
4
5
6
7

plt.figure(figsize=(8, 6))
plt.plot(n_values, energy_levels, marker='o', linestyle='-')
plt.title('Bohr Model Energy Levels')
plt.xlabel('Principal Quantum Number (n)')
plt.ylabel('Energy (J)')
plt.grid(True)
plt.show()

• Matplotlibを使ってグラフを作成し、エネルギー準位を表示しています。
• plt.figure(figsize=(8, 6)) でグラフのサイズを設定します。
• plt.plot で n_values に対する energy_levels をプロットし、マーカー ‘o’ を使用してデータ点を示し、直線でデータ点をつなぎます。
• グラフのタイトル、軸ラベルを設定し、グリッドを表示しています。
• plt.show() でグラフを表示します。

結果解説

[実行結果]

このグラフは、ボーアの原子模型に基づいて計算された原子のエネルギー準位を示しています。

以下は、グラフに表示される内容の詳細な説明です。

1. x軸:

• x軸は主量子数(n)を表しています。
  主量子数は、電子が原子の中心から離れた軌道またはエネルギー準位を示します。
  主量子数が大きくなるにつれて、電子のエネルギー準位が上昇します。

2. y軸:

• y軸はエネルギーを表しています。
  エネルギーはボーアの原子模型によって予測された値であり、主量子数(n)に依存します。
  負の値を持つことに注意してください。
  これは、電子が原子核に束縛されているため、系全体のエネルギーが負の値となるためです。

3. グラフのプロット:

• グラフには、主量子数(n)に対するエネルギー準位がプロットされています。
  各点は、特定の主量子数(n)に対応するエネルギーを示しています。
• マーカー ‘o’ が使用されていますが、これはデータ点を示すための円を意味します。
• 線はデータ点をつなぐための直線を表し、データの間の関係を視覚化します。

4. タイトル:

• グラフのタイトルは “Bohr Model Energy Levels” となっており、ボーアの原子模型に基づくエネルギー準位を示していることを示しています。

5. 軸ラベル:

• x軸は “Principal Quantum Number (n)” とラベル付けされており、主量子数(n)を示します。
• y軸は “Energy (J)” とラベル付けされており、エネルギーをジュール単位で示しています。

6. グリッド:

• グラフには背景にグリッドが表示されており、データ点の位置を見やすくし、目盛り線に沿ってデータを読み取るのを助けます。

このグラフは、主量子数(n)とエネルギーの関係を視覚化し、ボーアの原子模型に基づく原子のエネルギー準位の理解を支援します。

クラーク-ラムダ分布（Clark-Lambda Distribution）

クラーク-ラムダ分布（Clark-Lambda Distribution）は、確率分布の一種であり、リスク分析や信号処理などの分野で使用されます。

この分布の確率密度関数（PDF）は次のように定義されます:

f(x;λ)=2πλλ2+x2

ここで、(x)は確率変数であり、(λ)は分布のパラメータです。

以下は、Pythonでこの分布を解析し、グラフ化する方法の例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

import numpy as np
import matplotlib.pyplot as plt

def clark_lambda_distribution(x, lam):
    return (2 / np.pi) * (lam / (lam**2 + x**2))

# パラメータの設定
lam = 1.0  # λの値

# xの範囲を定義
x_values = np.linspace(-10, 10, 1000)

# 確率密度関数（PDF）を計算
pdf_values = clark_lambda_distribution(x_values, lam)

# グラフをプロット
plt.figure(figsize=(8, 6))
plt.plot(x_values, pdf_values, label=f'λ={lam}')
plt.title('Clark-Lambda Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

このコードは、−10から10までの範囲でClark-Lambda分布の確率密度関数を計算し、グラフ化します。

[実行結果]

Lambdaパラメータ（λ）を変更することで、異なる分布を観察できます。

ソースコード解説

ソースコードの各部分の説明します。

1. NumPyとMatplotlibのインポート:

1
2

import numpy as np
import matplotlib.pyplot as plt

• NumPyはPythonで数値計算を行うためのライブラリです。
• MatplotlibはPythonでグラフ描画を行うためのライブラリです。
  このスクリプトでは、Matplotlibのpyplotモジュールを使用しています。

2. Clark-Lambda分布の確率密度関数を定義する関数:

1
2

def clark_lambda_distribution(x, lam):
   return (2 / np.pi) * (lam / (lam**2 + x**2))

• clark_lambda_distribution 関数は、Clark-Lambda分布の確率密度関数を計算します。
  引数として x（確率変数）と lam（分布のパラメータ）を受け取ります。

3. パラメータの設定:

1

lam = 1.0  # λの値

• lam はClark-Lambda分布のパラメータ(λ)の値を示しています。

4. xの範囲を定義:

1

x_values = np.linspace(-10, 10, 1000)

• np.linspace 関数を使って、−10から10の範囲を等間隔で1000点に分割した x の値を生成します。
  これにより、確率密度関数のグラフが滑らかになります。

5. 確率密度関数（PDF）を計算:

1

pdf_values = clark_lambda_distribution(x_values, lam)

• 先ほど定義した clark_lambda_distribution 関数を使って、与えられた x の値とパラメータ(λ)に基づいてClark-Lambda分布の確率密度関数の値を計算します。

6. グラフをプロット:

1
2
3
4
5
6
7
8

plt.figure(figsize=(8, 6))
plt.plot(x_values, pdf_values, label=f'λ={lam}')
plt.title('Clark-Lambda Distribution')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.legend()
plt.grid(True)
plt.show()

• Matplotlibを使ってグラフを作成し、Clark-Lambda分布の確率密度関数を表示します。
• plt.figure(figsize=(8, 6)) でグラフのサイズを設定します。
• plt.plot で x_values と pdf_values をプロットし、ラベルにはパラメータ(λ)の値が表示されます。
• plt.title, plt.xlabel, plt.ylabel を使ってタイトルや軸のラベルを設定します。
• plt.legend() で凡例を表示します。
• plt.grid(True) でグリッドを有効にし、視覚的な参照を改善します。
• plt.show() でグラフを表示します。

結果解説

[実行結果]

グラフに表示される内容の詳細な説明です。

1. x軸:

• x軸は確率変数 (x)を表します。
  この確率変数はClark-Lambda分布におけるランダム変数であり、確率密度関数が評価される値の範囲が表示されます。
  ここでは、−10から10までの範囲が選択されています。

2. y軸:

• y軸は確率密度関数（PDF）の値を表します。

Clark-Lambda分布の確率密度関数は、(x)に関する確率密度を示し、y軸の値はその密度を表します。

3. ラベル:

• グラフにはClark-Lambda分布の確率密度関数が、指定されたLambdaパラメータ（λ）でプロットされています。
  ラベルにはこのパラメータの値が表示され、グラフ上で異なるパラメータの効果を直感的に理解するのに役立ちます。

4. 凡例:

• 複数のLambdaパラメータを使用する場合、それぞれの分布が区別できるように凡例が表示されます。
  この例では、唯一のLambdaパラメータが使用されていますが、複数の分布を比較する場合には凡例が重要です。

5. タイトル:

• グラフのタイトルには、プロットされている分布の種類が示されます。
  この場合、「Clark-Lambda Distribution」と表示されます。

6. グリッド:

• グラフには背景にグリッドが表示されます。
  これにより、目盛り線に沿ってデータを読み取るのが容易になります。

このグラフは、Clark-Lambda分布の確率密度関数を直感的に理解しやすくするためのものであり、異なるLambdaパラメータを使用することで、分布の形状がどのように変化するかを視覚的に把握できます。

オイラー-ラグランジュ方程式

オイラー-ラグランジュ方程式は、力学系の運動を記述する非線形常微分方程式です。

以下は、Pythonコードの例です。

このコードでは、scipy.integrateモジュールを使って常微分方程式を数値的に解き、matplotlibを使ってグラフを描画しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

# オイラー-ラグランジュ方程式
def euler_lagrange(y, t, m, k, g, l):
    theta, theta_dot = y
    dtheta_dt = theta_dot
    dtheta_dot_dt = -(g/l)*np.sin(theta) - (k/(m*l**2))*theta
    return [dtheta_dt, dtheta_dot_dt]

# 初期条件
theta0 = np.pi/4
theta_dot0 = 0
y0 = [theta0, theta_dot0]

# パラメータ
m = 1.0  # 質量
k = 1.0  # ばね定数
g = 9.81 # 重力加速度
l = 1.0  # 長さ

# 時間範囲
t = np.linspace(0, 20, 1000)

# 常微分方程式を解く
sol = odeint(euler_lagrange, y0, t, args=(m, k, g, l))

# グラフ描画
plt.figure(figsize=(10, 6))
plt.plot(t, sol[:, 0], 'b', label='theta(t)')
plt.plot(t, sol[:, 1], 'g', label='theta_dot(t)')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Solution')
plt.title('Euler-Lagrange Equation')
plt.show()

このコードを実行すると、時間tに対する変数thetaとtheta_dotのグラフが描画されます。
初期条件やパラメータを変更すると、異なる振る舞いが観察できます。

オイラー-ラグランジュ方程式は、非線形性があるため、解の振る舞いが複雑になる場合があります。
このコードでは、単振り子の運動を例として示しましたが、さまざまな力学系への応用が可能です。

必要に応じて、グラフの範囲やラベル、タイトルなどを調整してください。
また、より詳細な解析や可視化が必要な場合は、適宜コードを拡張できます。

オイラー-ラグランジュ方程式は、力学系の運動を記述する基本的な方程式であり、物理学や工学分野で広く使われています。

[実行結果]

ソースコード解説

ソースコードを詳しく説明します。

1. ライブラリのインポート

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint

• NumPyライブラリをnpという名前で、数値計算に使用します。
• matplotlibライブラリをpltという名前で、グラフ描画に使用します。
• scipy.integrateモジュールからodeinitを、常微分方程式の数値解を求めるために使用します。

2. オイラー-ラグランジュ方程式の定義

1
2
3
4
5

def euler_lagrange(y, t, m, k, g, l):
    theta, theta_dot = y
    dtheta_dt = theta_dot
    dtheta_dot_dt = -(g/l)*np.sin(theta) - (k/(m*l**2))*theta
    return [dtheta_dt, dtheta_dot_dt]

• この関数では、オイラー-ラグランジュ方程式を定義しています。
• 入力引数yには、角度thetaと角速度theta_dotの値が渡されます。
• tは時間、m、k、g、lはそれぞれ質量、バネ定数、重力加速度、長さです。
• 方程式の右辺は、dtheta_dtとdtheta_dot_dtで表されています。
• 関数の出力は、dtheta_dtとdtheta_dot_dtのリストです。

3. 初期条件と系のパラメータの設定

1
2
3
4
5
6
7
8

theta0 = np.pi/4
theta_dot0 = 0
y0 = [theta0, theta_dot0]

m = 1.0  # 質量
k = 1.0  # ばね定数
g = 9.81 # 重力加速度
l = 1.0  # 長さ

• 初期条件として、theta0とtheta_dot0をそれぞれπ/4(約45度)と0(静止状態)に設定しています。
• y0は初期値のリストです。
• m、k、g、lには、質量、バネ定数、重力加速度、長さの値を代入しています。

4. 時間範囲の設定と常微分方程式の解法

1
2

t = np.linspace(0, 20, 1000)
sol = odeint(euler_lagrange, y0, t, args=(m, k, g, l))

• tには、0から20秒までの1000個の時間点が等間隔で設定されます。
• odeiintを使って、オイラー-ラグランジュ方程式の数値解sol が計算されます。
• 関数euler_lagrangeと初期値y0、時間範囲tが引数として渡されます。
• さらに、m、k、g、lの値もargsで渡されます。

5. グラフの描画

1
2
3
4
5
6
7
8

plt.figure(figsize=(10, 6))
plt.plot(t, sol[:, 0], 'b', label='theta(t)')
plt.plot(t, sol[:, 1], 'g', label='theta_dot(t)')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Solution')
plt.title('Euler-Lagrange Equation')
plt.show()

• 新しい図ウィンドウが、サイズ(10,6)インチで作成されます。
• sol[:, 0]は、thetaの解の時間変化を表す配列です。
• sol[:, 1]は、theta_dotの解の時間変化を表す配列です。
• それぞれ青と緑の線で描画されます。
• 凡例が配置され、ラベルが付けられます。
• 横軸のラベルは’Time’、縦軸のラベルは’Solution’です。
• グラフのタイトルは’Euler-Lagrange Equation’に設定されています。
• plt.show()で、グラフが表示されます。

このコードでは、オイラー-ラグランジュ方程式を使って単振り子の運動を記述し、その解の時間変化をグラフで可視化しています。

初期条件やパラメータを変更することで、異なる振る舞いを観察できます。

結果解説

[実行結果]

グラフには、2つの曲線が表示されています。

1. 青色の曲線: theta(t)

この曲線は、時間tに対する角度theta(単位はラジアン) の変化を表しています。
theta(t)は、オイラー-ラグランジュ方程式の第1変数です。
この例では、初期値theta0 = π/4 = 0.785ラジアン(約45度)から始まっています。
曲線の挙動は、単振り子の振動を表しています。

2. 緑色の曲線: theta_dot(t)

この曲線は、時間tに対する角速度theta_dot(単位はラジアン/秒) の変化を表しています。
theta_dot(t)は、オイラー-ラグランジュ方程式の第2変数です。
この例では、初期値theta_dot0 = 0 (静止状態)から始まっています。
曲線の挙動は、単振り子の振動の速さの変化を表しています。

グラフの横軸は時間tを表し、単位は秒です。
縦軸は、青曲線ではthetaの値(ラジアン)、緑曲線ではtheta_dotの値(ラジアン/秒)を表します。

曲線の挙動は、以下のパラメータによって決まります。

• m = 1.0 (質量)
• k = 1.0 (バネ定数)
• g = 9.81 (重力加速度)
• l = 1.0 (単振り子の長さ)

これらのパラメータを変更すると、曲線の振る舞いが変化します。

つまり、このグラフは単振り子の運動をオイラー-ラグランジュ方程式で記述し、その解の時間変化を可視化したものです。

力学の分野で重要な役割を果たすこの方程式の振る舞いを、視覚的に確認できます。

ケーリー方程式

ケーリー方程式は以下の方程式で表されます。

y2=x3+ax+b

ここで、a、bは定数です。

この方程式は以下の特徴を持っています。

• 左辺のy2は2次式、右辺のx3+ax+bは3次式なので、この方程式は代数曲線を表しています。
• 特に、この曲線は楕円曲線と呼ばれる特殊な形状をしています。
  楕円は円に似た閉じた曲線です。
• a、bの値を変えると、楕円の形状が変わります。
• 楕円曲線上の点の集合は、加算やスカラー倍といった代数的な演算を定義できる代数構造になっています。
• この性質から、楕円曲線は暗号理論などの応用分野で重要な役割を果たしています。

つまり、ケーリー方程式は単に楕円曲線の方程式を表しているだけでなく、楕円曲線の持つ豊富な代数的構造を含んでいるのです。

簡単な方程式ながら、非常に深遠な数学的性質を持っているということができます。

ソースコード

Pythonでケーリー方程式を描画するコードは以下のようになります。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

import matplotlib.pyplot as plt
import numpy as np

# 定数a、bを設定
a = 1
b = 1

# x、yの範囲を設定
x_range = np.linspace(-10, 10, 1000)
y_range = np.linspace(-10, 10, 1000)

# グリッド上の各点でy^2 = x^3 + ax + bを計算
X, Y = np.meshgrid(x_range, y_range)
Z = Y**2 - (X**3 + a*X + b)

# 等高線を描画
plt.contour(X, Y, Z, [0])
plt.title(f"Weierstrass Elliptic Curve: y^2 = x^3 + {a}x + {b}")
plt.xlabel("x")
plt.ylabel("y")
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.show()

このコードでは、最初に定数a、bを設定しています。

次に、x、yの範囲を設定し、それぞれの点でケーリー方程式の値を計算しています。

その後、plt.contour関数を使って等高線を描画しています。
等高線の値が0の場合がちょうどケーリー方程式を満たす点になります。

最後に、グラフのタイトルと軸のラベルを設定し、x軸とy軸を描画しています。

実行すると、以下のようなグラフが表示されます。

[実行結果]

このグラフは、a=1、b=1のときのケーリー方程式を表しています。
aやbの値を変更すると、楕円曲線の形状が変わります。

グラフ解説

グラフを詳しく説明します。

1. 曲線の形状

• グラフには曲線が描かれています。
  これがケーリー方程式 y^2 = x^3 + ax + b (ここでは a=1, b=1) を満たす点の集合です。
• 曲線の形状は、楕円に似た閉じた曲線になっています。
  これは楕円曲線の典型的な形状です。
• 曲線は原点(0,0)を通っています。これは、
  原点がケーリー方程式を自動的に満たすためです。

2. 対称性

• 曲線は x 軸と y 軸に対して点対称になっています。
  これは、ケーリー方程式が x と y に関して対称であることに由来します。
• また、曲線は原点に関しても点対称になっています。

3. 交点

• 曲線は x 軸上の 3 点(−2.49,0)、(0,0)、(2.49,0)で交わっています。
  これらの点は、方程式 y^2 = x^3 + x + 1 を満たす y=0 の解になっています。

4. 漸近線

• 曲線は x 軸や y 軸に漸近線を持ちません。
  つまり、無限遠で軸に近づくことはありません。

5. グリッド線

• グラフには x 軸と y 軸が黒色の太い線で描かれています。
  これにより、曲線の位置を視覚的に捉えやすくなっています。

6. 軸のラベル

• x 軸のラベルは “x”、y 軸のラベルは “y” と付けられています。

7. タイトル

• グラフのタイトルは “Weierstrass Elliptic Curve: y^2 = x^3 + x + 1” と表示されています。
  これにより、このグラフがケーリー方程式の特定のケース (a=1, b=1) を表していることがわかります。

このように、この単純な曲線グラフからも、ケーリー方程式や楕円曲線の様々な性質を読み取ることができます。