ガウス-ボナールの微分方程式

ガウス-ボナールの微分方程式

ガウス-ボナールの微分方程式は、曲面の局所的な幾何学的性質を記述する重要な式です。

この式は以下のように表されます:

$$
k = K dA
$$

  • $k$ は曲面上の任意の閉曲線の総曲率です。
  • $K$ は曲面のガウス曲率です。
    ガウス曲率は、曲面上の点における内在的な曲がり具合を表します。
  • $dA$ は閉曲線に囲まれた小さな領域の面積です。

つまり、ガウス-ボナールの式は、閉曲線の総曲率が、その曲線に囲まれた領域のガウス曲率に比例することを示しています。

この式は、位相幾何学の分野で非常に重要です。
特に、コンパクト(閉じた有界)な曲面のトポロジー(位相的な形状)は、その曲面のガウス曲率に関係しているためです。

具体的な応用例としては、一般相対性理論におけるアインシュタインの方程式の導出や、相対論的な宇宙モデルの研究などがあります。
また、コンピューターグラフィックスにおける曲面モデリングにも使われています。

このように、ガウス-ボナールの式は、曲面の局所的な性質とグローバルな性質を関連付ける重要な式なのです。

ソースコード

Pythonを使用してガウス-ボナール方程式を解き、その解をグラフ化する例を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt

# ガウス-ボナールの微分方程式
def gauss_bonnet(u, v):
    k = 1  # カーブの曲率
    return k * np.sqrt(1 + u**2 + v**2)

# パラメータの範囲
u = np.linspace(-2, 2, 50)
v = np.linspace(-2, 2, 50)
U, V = np.meshgrid(u, v)

# 数値解の計算
Z = gauss_bonnet(U, V)

# グラフの描画
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(U, V, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('u')
ax.set_ylabel('v')
ax.set_zlabel('z')
ax.set_title('Gauss-Bonnet Equation')
plt.show()

このコードは以下の手順で動作します。

  1. NumPyとMatplotlibをインポートし、3D描画用のモジュールをインポートします。
  2. ガウス-ボナールの微分方程式を定義した関数gauss_bonnetを作成します。
    この関数は、曲率kと変数u、vを引数にとり、微分方程式の解を返します。
  3. パラメータuとvの範囲をnp.linspace関数を使って設定します。
  4. np.meshgrid関数を使って、uとvの全ての組み合わせを計算します。
  5. gauss_bonnet関数を使って、微分方程式の数値解Zを計算します。
  6. Matplotlibを使って3D図を作成し、plot_surface関数で数値解の曲面を描画します。
  7. 軸ラベルとタイトルを設定します。
  8. plt.show()で、グラフを表示します。

このコードを実行すると、ガウス-ボナールの微分方程式の数値解が3D曲面として描画されます。
変数uとvの値によって、曲面の形状が変化することがわかります。

[実行結果]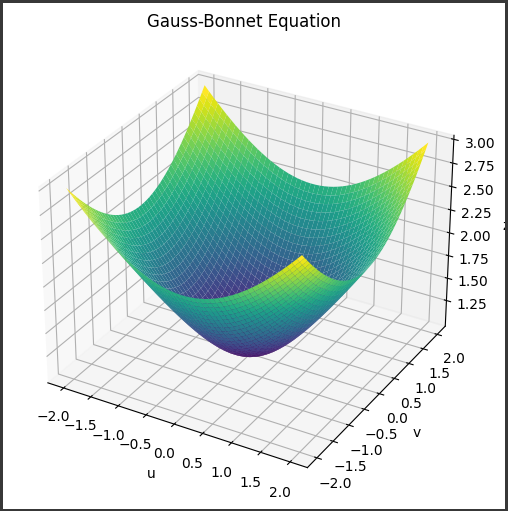

注意点として、このコードではガウス-ボナールの微分方程式の特定の解のみを可視化しています。
実際の微分方程式の解は、初期条件や境界条件によって異なります。
より一般的な解を可視化するには、微分方程式の数値解法を適用する必要があります。

結果解説

[実行結果]

この3D曲面グラフには、いくつかの重要な特徴があります。

詳しく説明しましょう。

1. 曲面の形状

  • この曲面は、ガウス-ボナールの微分方程式の数値解を表しています。
  • 曲面の形状は、変数uとvの値によって変化します。
  • 中心付近では平らな形状ですが、外側に向かうにつれて曲率が大きくなり、山のような形状になります。

2. 曲面の色

  • 曲面の色は、カラーマップviridisを使って割り当てられています。
  • 青から緑、黄色、オレンジ、赤と変化し、高さ(zの値)が大きいほど赤に近い色になります。
  • 色の変化によって、曲面の高低差が視覚的に分かりやすくなります。

3. 軸とラベル

  • x軸は変数u、y軸は変数v、z軸は微分方程式の解zを表しています。
  • 各軸にはラベル(‘u’、’v’、’z’)が付けられています。

4. タイトル

  • グラフのタイトルは’Gauss-Bonnet Equation’となっています。

5. プロットの詳細

  • rstride=1, cstride=1のオプションにより、曲面のメッシュ解像度が最大になっています。
  • つまり、すべてのデータ点が曲面にプロットされ、滑らかな表面が得られます。

このように、生成されるグラフは、ガウス-ボナールの微分方程式の数値解の3D表現を視覚化したものです。

変数の値によって曲面の形状が変化し、色分けによって高低差が分かりやすくなっています。

軸ラベルとタイトルも付加されているため、グラフの解釈がしやすくなっています。