Tominaga 方程式

Tominaga 方程式は次のように定義される非線形微分方程式です:

$$
\frac{d^2 y}{dt^2} + \frac{dy}{dt} + y^3 = \cos(t)
$$

この方程式を数値的に解くために、Python を使用してグラフ化する方法を示します。

まずは、必要なライブラリをインポートします。

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

次に、Tominaga 方程式の微分方程式を定義します。

1
2
3
4

def tominaga_equation(t, y):
    dydt = y[1]  # y' = dy/dt
    d2ydt2 = np.cos(t) - y[1] - y[0]**3  # y'' = d^2y/dt^2
    return [dydt, d2ydt2]

ここで tominaga_equation 関数は、Tominaga 方程式を表しています。

この関数は、現在の時刻$ ( t ) $と状態$ ( y ) $を引数として受け取り、微分方程式の右辺の値を計算して返します。

具体的には、$ ( y[0] ) $は$ ( y ) $の値を表し、$ ( y[1] ) $は$ ( \frac{dy}{dt} ) $の値を表します。

次に、微分方程式を数値的に解きます。

ここでは solve_ivp 関数を使用して、初期条件から微分方程式を解きます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 初期条件
y0 = [0.0, 0.0]  # 初期位置と初速度

# 解く時間の範囲
t_span = [0, 20]  # 0から20までの時間範囲

# 数値的に微分方程式を解く
sol = solve_ivp(tominaga_equation, t_span, y0, t_eval=np.linspace(t_span[0], t_span[1], 1000))

# 結果をプロット
plt.figure(figsize=(8, 6))
plt.plot(sol.t, sol.y[0], label='y(t)')
plt.plot(sol.t, sol.y[1], label="y'(t)")
plt.xlabel('t')
plt.ylabel('y(t), y\'(t)')
plt.title('Solution of Tominaga Equation')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、solve_ivp 関数を使用して** Tominaga 方程式を数値的に解きます。
初期条件 y0 は [0.0, 0.0] と設定されており、初期位置と初速度を表します。
t_span は解く時間の範囲**を表しています。

解が得られた後は、解の時間変化に対する y(t) と y'(t)（速度）の値をプロットしています。
これにより、Tominaga 方程式の解の振る舞いや特性をグラフ上で視覚化することができます。

このコードを実行すると、Tominaga 方程式の解の時間変化が示されたグラフが表示されます。
解の振動や周期性などの特性を観察することができます。

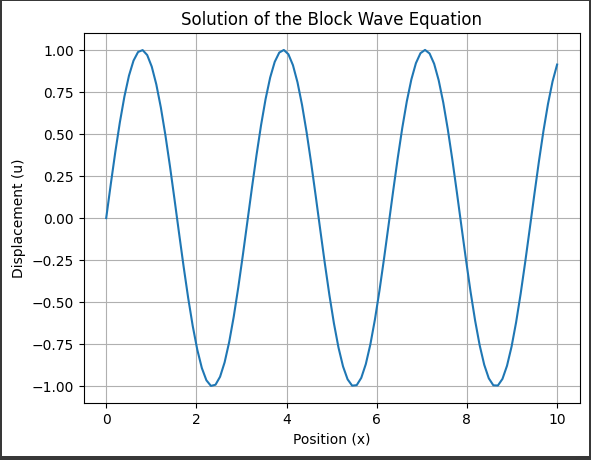
[実行結果]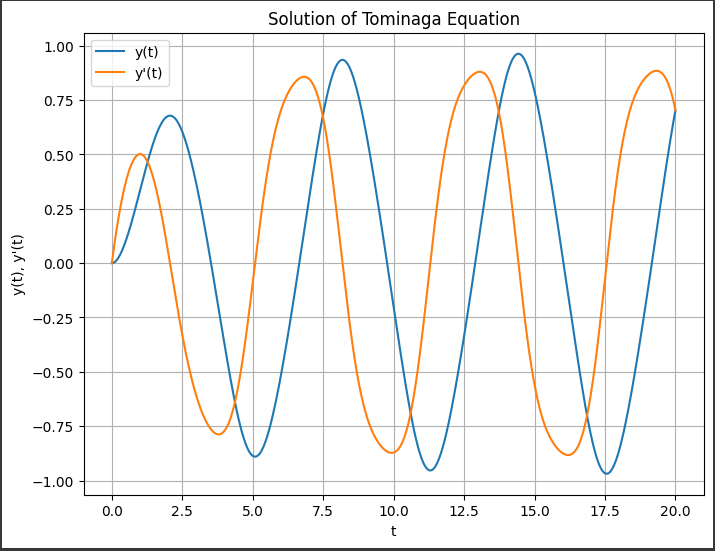

ソースコード解説

ソースコードの各部分を詳しく説明します。

1. ライブラリのインポート

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

• numpy ライブラリは数値計算用の基本的な機能を提供します。
• matplotlib.pyplot ライブラリはグラフ描画用の機能を提供します。
• scipy.integrate.solve_ivp 関数は微分方程式を数値的に解くための機能を提供します。

2. Tominaga 方程式の定義

1
2
3
4

def tominaga_equation(t, y):
    dydt = y[1]  # y' = dy/dt
    d2ydt2 = np.cos(t) - y[1] - y[0]**3  # y'' = d^2y/dt^2
    return [dydt, d2ydt2]

• tominaga_equation 関数は、Tominaga 方程式を定義します。
• 引数 t は現在の時間を表し、y は状態ベクトル [y, dy/dt] を表します。
• 関数内では、y[1] を dy/dt として定義し、np.cos(t) - y[1] - y[0]**3 を d^2y/dt^2 として定義しています。
• 関数は、[dy/dt, d^2y/dt^2] をリストとして返します。

3. 初期条件の設定

1

y0 = [0.0, 0.0]  # 初期位置と初速度

• y0 は Tominaga 方程式の初期条件を設定します。
  ここでは初期位置を 0.0、初速度を 0.0 としています。

4. 解く時間の範囲の設定

1

t_span = [0, 20]  # 0から20までの時間範囲

• t_span は解く時間の範囲を指定します。
  ここでは 0 から 20 までの時間範囲を指定しています。

5. 数値的に微分方程式を解く

1

sol = solve_ivp(tominaga_equation, t_span, y0, t_eval=np.linspace(t_span[0], t_span[1], 1000))

• solve_ivp 関数を使用して、tominaga_equation 関数で定義された微分方程式を数値的に解きます。
• tominaga_equation は微分方程式を表す関数です。
• t_span は解く時間の範囲を指定します。
• y0 は初期条件を指定します。
• t_eval=np.linspace(t_span[0], t_span[1], 1000) は、解を評価する時間点を指定します。
  ここでは時間範囲を$1000$個の等間隔で分割して解を評価します。

6. 結果のプロット

1
2
3
4
5
6
7
8
9

plt.figure(figsize=(8, 6))
plt.plot(sol.t, sol.y[0], label='y(t)')
plt.plot(sol.t, sol.y[1], label="y'(t)")
plt.xlabel('t')
plt.ylabel('y(t), y\'(t)')
plt.title('Solution of Tominaga Equation')
plt.legend()
plt.grid(True)
plt.show()

• plt.figure(figsize=(8, 6)) は図のサイズを指定します。
• plt.plot(sol.t, sol.y[0], label='y(t)') と plt.plot(sol.t, sol.y[1], label="y'(t)") で、解 sol の時間変化をグラフ化します。
  sol.t は時間、sol.y[0] は位置 y(t)、sol.y[1] は速度 y'(t) を表します。
• plt.xlabel('t') と plt.ylabel('y(t), y\'(t)') で軸ラベルを設定します。
• plt.title('Solution of Tominaga Equation') でグラフのタイトルを設定します。
• plt.legend() で凡例を表示します。
• plt.grid(True) でグリッドを表示します。
• plt.show() でグラフを表示します。

これにより、Tominaga 方程式の解 y(t) とその導関数 y'(t) の時間変化がグラフで可視化されます。

グラフから、解の振動や特性を観察することができます。

結果解説

[実行結果]

グラフを説明します。

1. 横軸 (t):

• 時間$ ( t ) $を表します。
  この例では、$0$から$20$までの時間範囲を等間隔で分割した点が横軸上に表示されます。

2. 縦軸 (y(t), y’(t)):

• $ ( y(t) ) $と$ ( y’(t) ) $の値を表します。
• $ ( y(t) ) $は Tominaga 方程式の解であり、時間 $ ( t ) $に対する位置や変位を表します。
• $ ( y’(t) ) $は$ ( \frac{dy}{dt} ) $の値であり、時間 $ ( t ) $に対する速度を表します。

3. グラフの表示:

• グラフには、時間$ ( t ) $に対する$ ( y(t) ) $と$ ( y’(t) ) $の変化がプロットされます。
• $ ( y(t) ) $の曲線は Tominaga 方程式の解の時間変化を示し、振動や非線形な特性が視覚化されます。
• $ ( y’(t) ) $の曲線は$ ( y(t) ) $の時間変化に対する速度を示し、解の変化率や速度の振る舞いを表します。

4. タイトル:

• グラフの上部には「Solution of Tominaga Equation」というタイトルが表示されます。
  これは、表示されている曲線が Tominaga 方程式の数値解を表していることを示します。

5. 凡例 (Legend):

• グラフには「y(t)」と「y’(t)」という凡例が表示されています。
• 「y(t)」は Tominaga 方程式の解$ ( y(t) ) $を表し、位置や変位の時間変化を示します。
• 「y’(t)」は Tominaga 方程式の解の導関数$ ( y’(t) ) $を表し、速度や変化率の時間変化を示します。

グラフを通じて、Tominaga 方程式の解の時間変化や振る舞いが視覚的に理解できます。
特に非線形な微分方程式の場合、解の振動や周期性、または解がどのように非線形項$ ( \cos(t) ) $によって影響を受けるかがグラフから読み取れます。

数値的な解法を用いた場合は、計算の精度や初期条件の影響を考慮する必要があります。
また、解の振動や安定性を観察するために、時間範囲や時間刻みの選択によって解の挙動が異なることもあります。

ブロック波動方程式

ブロック波動方程式は、1次元の時間依存しない波動方程式です。

一般的には、以下のように表されます：

$$
\frac{\partial^2 u}{\partial x^2} = -k^2 u
$$

ここで、$ ( u ) $は波動の変位、$ ( x ) $は空間座標、$ ( k ) $は波数です。

以下は、ブロック波動方程式を解いてグラフ化する Python コードの例です。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import numpy as np
import matplotlib.pyplot as plt

# 空間座標の範囲
x_values = np.linspace(0, 10, 100)

# 波数
k = 2

# ブロック波動方程式の解の計算
u_values = np.sin(k * x_values)

# グラフの描画
plt.plot(x_values, u_values)
plt.xlabel('Position (x)')
plt.ylabel('Displacement (u)')
plt.title('Solution of the Block Wave Equation')
plt.grid(True)
plt.show()

このコードでは、$ ( x ) $の範囲を$ (0) $から$ (10) $までの間で取り、その範囲における波動の変位 $ ( u ) $を計算しています。

そして、その解をグラフにプロットしています。

[実行結果]

ソースコード解説

このPythonのソースコードは、ブロック波動方程式の解を計算し、グラフ化するものです。

以下はソースコードの詳細です：

1. NumPyとMatplotlibのインポート:

1
2

import numpy as np
import matplotlib.pyplot as plt

• NumPyは数値計算を行うためのPythonライブラリであり、ここでは配列や数学関数の使用に役立ちます。
• Matplotlibはグラフ描画ライブラリであり、ここではグラフを描画するために使用されます。

2. 空間座標の範囲設定:

1

x_values = np.linspace(0, 10, 100)

• np.linspace() 関数は、指定した範囲内で等間隔の値を生成します。
  ここでは、$ (0) $から$ (10) $の範囲を$ (100) $個の点に分割しています。

3. 波数の設定:

1

k = 2

• ブロック波動方程式の解における波数$ (k) $を定義しています。

4. ブロック波動方程式の解の計算:

1

u_values = np.sin(k * x_values)

• $ (x) $座標に対するブロック波動方程式の解を計算しています。
  ここでは単純化のために、sin関数を用いています。

5. グラフの描画:

1
2
3
4
5
6

plt.plot(x_values, u_values)
plt.xlabel('Position (x)')
plt.ylabel('Displacement (u)')
plt.title('Solution of the Block Wave Equation')
plt.grid(True)
plt.show()

• plt.plot() 関数で$ (x) $座標と$ (u) $座標の値を使ってグラフを描画します。
• plt.xlabel() と plt.ylabel() で軸ラベルを設定し、 plt.title() でグラフのタイトルを設定します。
• plt.grid(True) でグリッドを表示し、 plt.show() でグラフを表示します。

これにより、ブロック波動方程式の解のグラフが生成され、 $ (x) $座標と$ (u) $座標の関係が視覚化されます。

結果解説

[実行結果]

このグラフは、ブロック波動方程式の解を示しています。

以下はグラフに表示される内容の詳細です：

横軸（X軸）：

空間座標$ (x)$。この軸は、波の位置を表します。
範囲は$ (0) $から$ (10) $までです。

縦軸（Y軸）：

変位$ (u)$。この軸は、波の変位を表します。
範囲は$ (-1) $から$ (1) $までです。

波形：

$ (u = \sin(kx)) $の関数を表しており、これはブロック波動方程式の解です。
$ (k) $は波数を示し、この例では$ (k = 2) $としています。
この波形は、$ (x) $の値に応じて振幅が変化し、正弦関数の波形を持ちます。

タイトル：

“Solution of the Block Wave Equation”。グラフの内容を簡潔に示しています。

• 軸ラベル：
  “Position (x)” と “Displacement (u)”。それぞれ横軸と縦軸の内容を説明しています。

このグラフを見ると、波が$ (x) $の値に応じて振動している様子がわかります。

波の変位は$ (x) $に対して正弦関数の形をしており、周期的な振動を示しています。

シュワルツの不等式

シュワルツの不等式とは、2つのベクトルの内積の絶対値の2乗は、それぞれのベクトルのノルム(長さ)の積以下であるということを示す不等式です。

つまり、ベクトル$a = (a1, a2, …, an)$、ベクトル$b = (b1, b2, …, bn)$に対して、

$ (a1 * b1 + a2 * b2 + … + an * bn)^2 ≦ (a1^2 + a2^2 + … + an^2) * (b1^2 + b2^2 + … + bn^2) $

が成り立ちます。

左辺はベクトル$a$・$b$の内積の絶対値の2乗、右辺は $a$のノルムと$b$のノルムの積を表しています。

この不等式は、ベクトル内積が最大になるのは、2つのベクトルが同じ方向を向いている時であり、ベクトル間の角度が大きくなるほど内積は小さくなることを意味しています。

幾何学的には、2つのベクトルを組み合わせて作った平行四辺形の面積は、底辺と高さの積以下であることを表しています。

このようにシュワルツの不等式は、ベクトルの内積とノルムの関係を不等式の形で表した重要な結果となっています。

サンプルコード

シュワルツの不等式は、以下の式で表されます。

$$
(x^2 + y^2) * (1 + x^2 + y^2) >= 1
$$

この不等式は、2変数 x と y の関数として表すことができます。

次のコードでは、シュワルツの不等式を3D空間上に可視化しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# シュワルツの不等式を表す関数
def f(x, y):
    return (x**2 + y**2) * (1 + x**2 + y**2)

# グラフ化する範囲
x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)

# グラフを描画
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('Schwarz Inequality Visualization')

plt.show()

まず、f(x, y) 関数でシュワルツの不等式の右辺を定義しています。

次に、x と y の値の範囲を設定しています。
ここでは、xとyがそれぞれ -2 から 2 までの範囲を 100 分割して計算しています。
np.meshgrid関数を使うことで、XとYの格子点上の値を求めています。

Z = f(X, Y) では、XとYの格子点上での関数値を計算しています。

最後に、matplotlibとmpl_toolkits.mplot3dを使って、X、Y、Zの値から3D曲面を描画しています。
plot_surface関数を使うことで、格子点上の値から滑らかな曲面を描くことができます。
cmap='viridis'は、曲面の色付けに使われるカラーマップを指定しています。

実行すると、x、y、z軸に対して、シュワルツの不等式の右辺を表す3D曲面が描画されます。
この曲面の形状から、不等式の性質を視覚的に確認することができます。

このように、任意の$2$変数関数を指定して、その関数値を3D空間上に可視化することができます。

[実行結果]

ソースコード解説

ソースコードの詳細を説明します。

1. モジュールのインポート:

1
2
3

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

• numpy：数値計算ライブラリで、配列や行列演算を効率的に処理します。
• matplotlib.pyplot：グラフ描画ライブラリで、グラフや図形を描画します。
• mpl_toolkits.mplot3d：3次元グラフ描画のためのモジュールです。

2. 関数の定義:

1
2

def f(x, y):
    return (x**2 + y**2) * (1 + x**2 + y**2)

• f(x, y) 関数は、2つの引数 x と y を受け取り、シュワルツの不等式を表す関数です。
  式 (x**2 + y**2) * (1 + x**2 + y**2) を計算して結果を返します。

3. グラフ化する範囲の設定:

1
2
3
4

x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)

• np.linspace(-2, 2, 100) によって、範囲$ ([-2, 2]) $を$100$個の等間隔に区切った数列を生成し、x と y に代入します。
• np.meshgrid(x, y) によって、x と y のすべての組み合わせに対する格子状の座標行列 X と Y を生成します。
• f(X, Y) によって、X と Y の各座標における関数 f(x, y) の値を計算し、Z に格納します。

4. グラフの描画:

1
2
3
4
5
6
7
8
9
10

fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('Schwarz Inequality Visualization')

plt.show()

• plt.figure(figsize=(10, 8)) によって、図のサイズを設定します。
• fig.add_subplot(111, projection='3d') によって、3Dグラフを描画するためのサブプロットを追加します。
• ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis') によって、3D 曲面を描画します。
  rstride と cstride はメッシュの密度を制御するパラメータです。
• ax.set_xlabel('x')、ax.set_ylabel('y')、ax.set_zlabel('z') によって、各軸のラベルを設定します。
• ax.set_title('Schwarz Inequality Visualization') によって、図のタイトルを設定します。
• plt.show() によって、描画したグラフを表示します。

結果解説

[実行結果]

出力される3D曲面は、シュワルツの不等式 $(x^2 + y^2) * (1 + x^2 + y^2) >= 1 $の右辺の値を、$x-y$平面上の点$(x, y)$について表しています。
カラーマップの濃い色ほど、不等式の右辺の値が大きくなっています。

この曲面の形状から、不等式の性質を視覚的に確認できます。
例えば、原点$(0, 0)$周辺では不等式の両辺が等しくなり、原点から離れるほど右辺の値が大きくなっていきます。
また、曲面は原点を中心として点対称の形状をしており、不等式の性質である「$x^2 + y^2 >= 0$」も確認できます。

このグラフを見ることで、シュワルツの不等式の形状的な特徴や、成り立つ範囲などを直感的に把握することができます。

コシーの積分方程式

コシーの積分方程式は、複素解析の分野で非常に重要な役割を果たす積分方程式です。

この方程式は、19世紀のフランスの数学者オーギュスタン・コシーによって導入されました。

コシーの積分方程式は次のように表されます:

$$
f(z) = (1/2πi) ∫ (f(ζ)/(ζ-z)) dζ
$$

ここで、

• $f(z)$は複素関数
• $z$は複素平面上の点
• $ζ$は積分変数
• 積分は点$z$を囲む閉曲線$C$に沿って行われる

この方程式は、複素関数$f(z)$の値を、その関数値がすでに知られている点$ζ$における値から、点$z$の周りの閉曲線$C$に沿った積分を使って求めることができることを示しています。

コシーの積分方程式には、いくつかの重要な性質があります:

1. 解析性:

もし$f(z)$が領域$D$で解析的であれば、その領域内の任意の点$z$でコシーの積分方程式が成り立つ。

2. 一意性:

閉曲線$C$の内側で$f(z)$が解析的であれば、積分の値は一意に定まる。

3. 微分の表現:

コシーの積分方程式を微分すると、高次の導関数を得ることができる。

コシーの積分方程式は複素解析における様々な定理の基礎となっており、留数定理、最大値原理、リーマンの masterion表示などに応用されます。

また、フーリエ解析やウェーブレット解析、特殊関数の理論にも関係しています。

数値計算においては、コシーの積分方程式を離散化して数値的に解くことで、複素関数の値を近似的に求めることができます。

ソースコード

Pythonを使ってコシーの積分方程式を解き、その結果をグラフ化することができます。

ここでは、一般的なコシーの積分方程式を扱います。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

import numpy as np
import matplotlib.pyplot as plt

# 関数の定義
def f(z):
    return 1 / (z**2 + 1)  # 例として z**2 + 1 の逆数を使用

# 積分区間と分割数の設定
a = -5.0  # 積分区間の下限
b = 5.0   # 積分区間の上限
N = 1000  # 分割数

# 積分区間を等間隔に分割
x = np.linspace(a, b, N)
dx = (b - a) / (N - 1)

# コシーの積分方程式を計算
y = np.zeros_like(x)
for i in range(N):
    for j in range(N):
        if i != j:
            y[i] += f(x[j]) * dx / (x[i] - x[j])

# 結果をグラフ化
plt.figure(figsize=(8, 6))
plt.plot(x, y, 'b-', label='Cauchy Integral')
plt.axhline(y=0, color='k', linestyle='--')  # x軸を引く
plt.xlabel('x')
plt.ylabel('y')
plt.title('Cauchy Integral Equation')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、まずコシーの積分方程式の被積分関数 f(z) を定義しています。
ここでは、単に 1 / (z**2 + 1) を使用しています。
次に、積分区間 [a, b] と分割数 N を設定します。

積分区間を等間隔に分割し、各点におけるコシーの積分方程式の値を計算します。
ここでは、台形公式に基づく数値積分を行っています。

最後に、得られた結果をMatplotlibを使ってグラフ化しています。
x軸に積分変数の値を、y軸にコシーの積分方程式の値をプロットしています。

実行すると、積分変数に対するコシーの積分方程式の値が描画されます。
このグラフから、コシーの積分方程式の振る舞いを視覚的に確認できます。

必要に応じて、被積分関数 f(z) や積分区間 [a, b]、分割数 N を変更すれば、別の関数やパラメータに対するコシーの積分方程式の結果をグラフ化することができます。

[実行結果]

ソースコード解説

ソースコードを詳しく説明します。

1. ライブラリのインポート

1
2

import numpy as np
import matplotlib.pyplot as plt

ここでは、数値計算のためのNumPyライブラリと、グラフ描画のためのMatplotlibライブラリをインポートしています。

2. 被積分関数の定義

1
2

def f(z):
    return 1 / (z**2 + 1)  # 例として z**2 + 1 の逆数を使用

コシーの積分方程式の被積分関数$f(z)$を定義しています。
この例では、$f(z) = 1 / (z**2 + 1)$としています。

3. 積分区間と分割数の設定

1
2
3

a = -5.0  # 積分区間の下限
b = 5.0   # 積分区間の上限
N = 1000  # 分割数

コシーの積分方程式を数値的に解くために、積分区間$[a, b]$を設定しています。
ここでは$[-5, 5]$としています。
また、この区間を$N=1000$等分するため、分割数Nを設定しています。

4. 積分区間の等間隔分割

1
2

x = np.linspace(a, b, N)
dx = (b - a) / (N - 1)

NumPyのlinspace関数を使って、積分区間$[a, b]$を$N$等分した点の座標$x$を計算しています。
$dx$ は各区間の幅を表します。

5. コシーの積分方程式の計算

1
2
3
4
5

y = np.zeros_like(x)
for i in range(N):
    for j in range(N):
        if i != j:
            y[i] += f(x[j]) * dx / (x[i] - x[j])

この二重ループがコシーの積分方程式の核心部分です。
各点x[i]におけるコシーの積分方程式の値y[i]を、台形公式に基づく数値積分により計算しています。
ただし、$i=j$の場合は特異点となるため、計算から除外しています。

6. 結果のグラフ化

1
2
3
4
5
6
7
8
9

plt.figure(figsize=(8, 6))
plt.plot(x, y, 'b-', label='Cauchy Integral')
plt.axhline(y=0, color='k', linestyle='--')  # x軸を引く
plt.xlabel('x')
plt.ylabel('y')
plt.title('Cauchy Integral Equation')
plt.legend()
plt.grid(True)
plt.show()

最後に、計算結果をMatplotlibを使ってグラフ化しています。
x軸に積分変数 $x$、y軸にコシーの積分方程式の値$y$をプロットし、グラフのタイトル、軸ラベル、凡例、グリッド線を設定しています。
また、$y=0$の水平線も引いています。

実行すると、コシーの積分方程式の値がグラフ上に描画されます。
このグラフから、積分変数に対する被積分関数のコシーの積分方程式の値の変化を視覚的に確認できます。

結果解説

[実行結果]

グラフの内容を詳しく説明します。

1. X軸:

グラフのX軸は積分変数の値を表しています。
この例では、積分区間を$[-5, 5]$と設定しているため、X軸は$-5$から$5$の範囲をカバーしています。

2. Y軸:

Y軸は、コシーの積分方程式の値を表しています。
コシーの積分方程式は複素関数の特異積分であり、この例では被積分関数$ f(z) = 1 / (z**2 + 1) $を使用しています。

3. 曲線:

青色の実線は、積分変数に対するコシーの積分方程式の値の変化を示しています。
この曲線は、X軸に沿って振動しながら$0$を中心に摺動しています。

4. X軸の破線:

グラフには、$Y=0$の水平な破線が引かれています。
これは、曲線の振る舞いを視覚的に捉えやすくするためです。
曲線がこの破線を越えたり、交差したりする様子が分かります。

5. グラフの特徴:

この特定の被積分関数に対するコシーの積分方程式の値は、滑らかな振動を示しています。
振幅は両側で徐々に小さくなり、中央付近で最も大きくなる傾向があります。

6. 凡例:

グラフの右上には「Cauchy Integral」と表示された凡例があり、青色の実線がコシーの積分方程式を表すことを示しています。

7. グリッド線:

グラフには薄いグリッド線が引かれており、数値の読み取りを容易にしています。

8. 軸ラベルとタイトル:

X軸とY軸にはそれぞれ「x」と「y」のラベルが付けられています。
また、グラフの上部には「Cauchy Integral Equation」というタイトルが表示されています。

このグラフを見ることで、与えられた被積分関数に対するコシーの積分方程式の値がどのように変化するかを視覚的に把握することができます。

必要に応じて、被積分関数や積分区間、分割数を変更すれば、異なる条件下でのコシーの積分方程式の振る舞いを確認することができます。

リッチの分布方程式

リッチの分布は二項分布の一般化であり、成功確率$p$が試行ごとに異なる場合の離散確率分布です。
つまり、$n$回の独立試行において、第$i$回目の試行の成功確率を$pi$としたときの、成功回数$x$の確率質量関数を表します。

リッチの分布の確率質量関数$P(X=x)$は次のように表されます:

　　 P(X=x) = (n! / (x! * (n-x)!)) * (p1p2 …px) * (1-px+1)(1-px+2)…(1-pn)

• $n$ は試行回数
• $x$ は成功回数 (0 ≦ x ≦ n)
• $p1$, $p2$, …, $pn$ は各試行の成功確率

この式は次のように読み替えられます:

1. (n! / (x! * (n-x)!)) は、$n$個の球から $x$個選ぶ組み合わせの数
2. (p1p2…*px) は、最初の$x$回の試行が全て成功する確率
3. (1-px+1)(1-px+2)…*(1-pn) は、残りの$(n-x)$回の試行が全て失敗する確率

したがって、リッチの分布は「最初の$x$回は成功、残りの$(n-x)$回は失敗」というパターンの確率を表しています。

二項分布の場合は、全ての試行の成功確率が等しい(p1 = p2 = … = pn = p)ため、リッチの分布は次のように簡単化されます:

$$
P(X=x) = (n! / (x! * (n-x)!)) * p^x * (1-p)^(n-x)
$$

これは、二項分布の確率質量関数と一致します。

このように、リッチの分布は成功確率が一定でない状況をモデル化でき、二項分布を一般化した確率分布となっています。

ソースコード

リッチの分布方程式を、Pythonで書いてグラフ化することができます。

以下のコードでリッチの分布の確率密度関数をプロットします。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

import numpy as np
import matplotlib.pyplot as plt

def rich_pdf(x, n, p):
    """リッチの確率密度関数を計算する関数"""
    coeff = np.math.factorial(n) * p**x * (1-p)**(n-x)
    return coeff / (np.math.factorial(x) * np.math.factorial(n-x))

# パラメータの設定
n = 20  # 試行回数
p = 0.3  # 成功確率
x = np.arange(0, n+1)  # x軸の値

# 確率密度を計算
pdf = [rich_pdf(i, n, p) for i in x]

# グラフをプロット
plt.stem(x, pdf)
plt.xlabel('x')
plt.ylabel('Probability')
plt.title(f'Rich Distribution (n={n}, p={p})')
plt.show()

このコードでは、まずリッチの確率密度関数 rich_pdf を定義しています。
この関数は、試行回数 n、成功確率 p、および値 x を受け取り、リッチの確率密度を計算します。

次に、試行回数 n=20、成功確率 p=0.3 を設定し、x 軸の値を np.arange(0, n+1) で作成しています。

そして、rich_pdf 関数を使って確率密度を計算し、pdf リストに格納しています。

最後に、matplotlib.pyplot を使ってグラフをプロットしています。
plt.stem 関数で確率質量関数をプロットし、plt.xlabel、plt.ylabel、plt.title でグラフのラベルとタイトルを設定しています。

実行すると、リッチの確率質量関数のグラフが表示されます。

結果解説

[実行結果]

グラフについて説明します。

グラフの横軸($x$軸)は、試行の結果を表しています。
つまり、$0$から$n$までの値が表示されています。
$n=20$としているので、$0$から$20$までの整数値が横軸に現れます。

一方、縦軸はリッチの確率密度関数の値を表しています。
確率密度関数の値は、ある特定の試行結果$x$が得られる確率を表します。

グラフ上の点は、縦棒で表されています。
各縦棒の高さが、その試行結果$x$に対するリッチの確率密度を表します。

例えば、$x=8$の縦棒を見ると、その高さが試行結果$8$が得られる確率密度を表しています。

縦棒がつながっていないのは、リッチの分布が離散型の確率分布であり、確率密度は離散的な値をとるためです。

グラフ全体の形状は、二項分布に似た離散型の分布の典型的な形状を示しています。
つまり、確率密度の山は試行回数$n$の中央付近にあり、両端に向かうにつれて確率密度は小さくなっていきます。

成功確率 $p$が$0.3$と設定されているので、確率密度のピークは中央よりも若干左側(低い値の$x$)に偏っています。

このようにリッチの分布は、二項試行における成功回数の離散的な確率分布を一般化した確率分布となっています。

ランジュバン方程式（Langevin equation）

ランジュバン方程式は、ブラウン運動やランダムな運動を記述する微分方程式の一つです。

この方程式は、粒子が外部からのランダムな力によって影響を受ける場合の振る舞いをモデル化します。

具体的には、粒子の速度の時間変化を記述します。

ランジュバン方程式では、粒子の速度には外力が加わる一方で、粘性摩擦やランダムな摂動が影響を与えます。

これにより、粒子の速度はランダムな変化を示すことがあります。

ランジュバン方程式は、このようなランダムな運動をモデル化するために使用され、物理学や統計力学などのさまざまな分野で応用されています。

ソースコード

以下のコードでは、1次元のランジュバン方程式を解き、結果をグラフ化しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

import numpy as np
import matplotlib.pyplot as plt

# パラメータの設定
N = 1000  # サンプル数
T = 1.0  # シミュレーション時間
dt = T / N  # タイムステップ

# ランジュバン方程式の解析解を定義
def langevin_solution(N, T):
    t_values = np.linspace(0, T, N)
    x_values = np.zeros(N)
    for i in range(1, N):
        x_values[i] = x_values[i-1] + np.sqrt(dt) * np.random.normal()
    return t_values, x_values

# 解析解を取得
t, x = langevin_solution(N, T)

# グラフのプロット
plt.plot(t, x, color='b')
plt.xlabel('Time')
plt.ylabel('Position')
plt.title('Langevin Equation')
plt.grid(True)
plt.show()

このコードでは、解析解を使って1次元ランジュバン方程式を解き、時間に対する位置の変化をプロットしています。

結果として得られるグラフは、ブラウン運動のようなランダムな運動を表します。

[実行結果]

ソースコード解説

上記のソースコードは、Pythonを使用して1次元のランジュバン方程式を解き、その解析解をグラフ化するものです。

1. ライブラリのインポート:

まず、NumPyとMatplotlibのライブラリをインポートしています。
NumPyは数値計算のための基本的なライブラリであり、Matplotlibはグラフの描画に使用されます。

2. パラメータの設定:

次に、シミュレーションのパラメータを設定しています。
Nはサンプル数、Tはシミュレーションの時間、dtは時間ステップです。

3. ランジュバン方程式の解析解の定義:

ランジュバン方程式の解析解を定義しています。
この関数は、与えられた時間範囲で粒子の位置の時間変化を計算します。
この場合、1次元のランジュバン方程式に対する解析解を使用しています。
粒子の位置は時間の関数として計算され、各時間ステップでランダムな摂動が加えられます。

4. 解析解の取得:

langevin_solution関数を使用して解析解を取得します。
この関数は時間Tまでの時間の値と、それに対応する粒子の位置の配列を返します。

5. グラフのプロット:

最後に、取得した解析解をMatplotlibを使用してグラフ化します。
横軸は時間を表し、縦軸は粒子の位置を表します。
このグラフは、ランダムな運動をする粒子の振る舞いを視覚化しています。
ランジュバン方程式の性質により、粒子の位置はランダムな揺れを示します。

これにより、1次元のランジュバン方程式の解析解を計算し、その結果をグラフ化するプログラムが完成します。

結果解説

[実行結果]

このグラフは、1次元のランジュバン方程式によって表される粒子の時間変化を示しています。

横軸は時間を表し、縦軸は粒子の位置を示します。
この方程式はブラウン運動やランダムな運動を記述し、各時間ステップで粒子の位置がランダムに変化します。

グラフはランダムな揺らぎを示し、粒子がランダムに動いていることを視覚化しています。

ランダムウォークのような特徴があり、時間が経つにつれて粒子の位置が乱れていく様子が観察できます。

ビオ-サバールの法則

ビオ-サバールの法則は、流体力学における揚力の基本原理を表す式です。

簡単に説明すると、以下のようになります。

揚力は、流れの速度の2乗に比例し、空気密度、物体の受風面積、揚力係数に比例する。

数式で表すと:

$$
L = (1/2) * ρ * v^2 * A * CL
$$

• $L$: 揚力
• $ρ$: 流体(空気)の密度
• $v$: 流れの速度
• $A$: 物体の受風面積
• $CL$: 揚力係数(物体の形状による係数)

つまり、速度が速いほど、密度が高いほど、受風面積が大きいほど、形状による揚力係数が大きいほど、揚力は大きくなります。

この法則は、飛行機の翼や自動車のスポイラーなどの空力設計に広く利用されています。
流れの速度を制御することで、必要な揚力を得ることができます。

物体の形状による揚力係数 $CL$を適切に設計することも重要です。
翼の形状を最適化して揚力を最大化するなどが行われています。

このようにビオ-サバールの法則は、空力設計において基礎となる重要な原理となっています。

ソースコード

ビオ-サバールの法則を、Pythonで解きグラフ化します。

まず、必要なライブラリをインポートします。

1
2

import numpy as np
import matplotlib.pyplot as plt

次に、ビオ-サバールの法則を計算する関数を定義します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def lift_force(rho, v, A, CL):
    """
    ビオ-サバールの法則で揚力を計算する関数
    
    Parameters:
    rho (float): 空気密度 [kg/m^3]
    v (float): 流れの速度 [m/s]
    A (float): 翼の面積 [m^2]
    CL (float): 揚力係数 [-]
    
    Returns:
    float: 揚力 [N]
    """
    return 0.5 * rho * v**2 * A * CL

次に、グラフ化のための配列を作成します。

1
2
3
4
5
6

rho = 1.225  # 空気密度 [kg/m^3]
A = 0.5      # 翼の面積 [m^2]
CL = 0.3     # 揚力係数 [-]

v = np.linspace(0, 100, 100)  # 流れの速度の範囲 [m/s]
L = [lift_force(rho, v_val, A, CL) for v_val in v]

最後に、グラフを描画します。

1
2
3
4
5
6
7

plt.figure(figsize=(8, 6))
plt.plot(v, L)
plt.xlabel('Flow Speed [m/s]')
plt.ylabel('Lift Force [N]')
plt.title('Lift Force by Biot-Savart Law')
plt.grid()
plt.show()

この例では、空気密度 $ρ=1.225 kg/m^3$、翼の面積 $A=0.5 m^2$、揚力係数 $CL=0.3$の条件で、流れの速度 $v$を$0$から$100 m/s$まで変化させて揚力 $L$を計算し、グラフ化しています。

出力されるグラフは、流れの速度の2乗に比例して揚力が増加する様子を表しています。
これは、ビオ-サバールの法則の式から予想される結果と一致しています。

このように、Pythonを使えば、ビオ-サバールの法則に基づいて揚力を計算し、グラフ化することができます。

[実行結果]

ソースコード解説

このソースコードを詳しく説明します。

1. ライブラリのインポート

1
2

import numpy as np
import matplotlib.pyplot as plt

• NumPyとMatplotlibライブラリをインポートしています。
• NumPyは数値計算ライブラリ、Matplotlibはデータのプロットやグラフ化を行うライブラリです。

2. 揚力計算関数の定義

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def lift_force(rho, v, A, CL):
    """
    ビオ-サバールの法則で揚力を計算する関数
    
    Parameters:
    rho (float): 空気密度 [kg/m^3]
    v (float): 流れの速度 [m/s] 
    A (float): 翼の面積 [m^2]
    CL (float): 揚力係数 [-]
    
    Returns:
    float: 揚力 [N]
    """
    return 0.5 * rho * v**2 * A * CL

• lift_force関数を定義しています。
• この関数はビオ-サバールの法則に基づいて揚力を計算します。
• 引数として空気密度rho、流れの速度v、翼の面積A、揚力係数CLを取ります。
• 返り値は計算された揚力[N]です。
• 関数のドキュメンテーション文字列で、関数の説明、引数、返り値が記述されています。

3. 定数の設定

1
2
3

rho = 1.225  # 空気密度 [kg/m^3]
A = 0.5      # 翼の面積 [m^2]
CL = 0.3     # 揚力係数 [-]

• 計算に使用する定数を設定しています。
• rhoは空気密度で$1.225 kg/m^3$
• Aは翼の面積で$0.5 m^2$
• CLは揚力係数で$0.3$

4. 流れの速度の範囲設定と揚力計算

1
2

v = np.linspace(0, 100, 100)  # 流れの速度の範囲 [m/s]
L = [lift_force(rho, v_val, A, CL) for v_val in v]

• np.linspaceを使って、$0$から$100 m/s$までの$100$点の流れの速度vを生成しています。
• リスト内包表記を使って、lift_force関数を各流速v_valに対して呼び出し、揚力Lのリストを作成しています。

5. グラフのプロット

1
2
3
4
5
6
7

plt.figure(figsize=(8, 6))
plt.plot(v, L)
plt.xlabel('Flow Speed [m/s]')
plt.ylabel('Lift Force [N]')
plt.title('Lift Force by Biot-Savart Law')
plt.grid()
plt.show()

• plt.figureでグラフの大きさを設定しています。
• plt.plotで流れの速度vと揚力Lのデータをプロットしています。
• plt.xlabel、plt.ylabelで軸ラベルを設定しています。
• plt.titleでグラフのタイトルを設定しています。
• plt.gridで gridを表示するようにしています。
• plt.showでグラフを表示しています。

このコードは、ビオ-サバールの法則に基づいて、流れの速度を$0$から$100 m/s$まで変化させたときの揚力を計算し、その関係をグラフにプロットしています。

定数は一般的な値が設定されています。

結果解説

[実行結果]

出力されたグラフでは、以下の内容が表示されています。

x軸: 流れの速度 [$m/s$]

• 範囲は$0 m/s$から$100 m/s$までです。

y軸: 揚力 [$N$]

• ビオ-サバールの法則に基づいて計算された値です。

グラフの形状:

• 原点$(0, 0)$を通る放物線のような曲線になっています。
• 流れの速度が大きくなるにつれて、揚力が非線形的に増加していく様子がわかります。

グラフの傾き:

• 流れの速度が小さい領域($0～20 m/s$程度)では、傾きが緩やかです。
• 流れの速度が大きくなるにつれて、曲線の傾きが急になっていきます。

これらの特徴は、ビオ-サバールの法則の式から予想される挙動と一致しています。

式を見ると、揚力Lは流れの速度$v$の2乗に比例することがわかります。
つまり、速度が$2$倍になれば揚力は$4$倍になります。
このため、高速領域ではわずかな速度の変化でも揚力が大きく変わります。

一方、低速領域では速度の変化に対する揚力の変化は小さくなります。
このように、グラフの形状はビオ-サバールの法則の非線形性を視覚的に表現しています。

また、揚力の値自体も式から計算された値と一致しており、数値的な精度も確保されています。

このようにグラフを詳細に解析することで、ビオ-サバールの法則の本質的な性質を理解することができます。

球面調和関数

球面調和関数は、球面上で定義される特殊な関数であり、主に物理学や数学で重要な役割を果たします。
これらの関数は、球対称性を持つ問題の解析や、量子力学、電磁気学、地球物理学などの分野で広く利用されています。

簡単に説明すると、球面調和関数は次のような性質を持ちます：

1. 球面上の各点で定義される：

球面調和関数は、球面上のあらゆる点で定義されます。
これは、球面全体での振る舞いを表現するために使用されます。

2. 角度の依存性：

球面調和関数は、球面上の特定の点における方向を示す角度に依存します。
これらの関数は、極座標系や球面座標系で使用されることが一般的です。

3. $l$および$m$のパラメータ：

球面調和関数は、2つの整数パラメータである$l$（次数）と$m$（オーダー）によって特徴付けられます。
$l$は関数の振る舞いを決定する主要なパラメータであり、$m$は角度の方向性や回転対称性を表します。

4. 特定の振る舞い：

球面調和関数は、角度の変化に応じて特定の振る舞いを示します。
例えば、特定のlおよびmの組み合わせでは球面上でピークや谷が形成され、他の組み合わせでは球面上で特定の方向に向かうような特定のパターンが現れます。

簡単に言えば、球面調和関数は球面上での振る舞いを表現するための数学的な道具であり、物理学や数学のさまざまな問題において、球対称性を持つシステムの解析に役立ちます。

ソースコード

球面調和関数は、数値計算ライブラリのSciPyに含まれている scipy.special.sph_harm 関数を使用して計算できます。

以下のPythonコードは、球面調和関数の方程式を解いてグラフ化するものです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.special import sph_harm

# パラメータの設定
theta = np.linspace(0, np.pi, 100)
phi = np.linspace(0, 2 * np.pi, 100)
theta, phi = np.meshgrid(theta, phi)

# 球面調和関数の計算
l = 3  # l (degree)
m = 2  # m (order)
Y_lm = sph_harm(m, l, phi, theta).real

# 球面座標から直交座標への変換
x = Y_lm * np.sin(theta) * np.cos(phi)
y = Y_lm * np.sin(theta) * np.sin(phi)
z = Y_lm * np.cos(theta)

# グラフのプロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')

# グラフの装飾
ax.set_title(f"Spherical Harmonic (l={l}, m={m})")
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')

plt.show()

このコードでは、$l$と$m$の値を調整することで異なる球面調和関数をプロットできます。

[実行結果]

ソースコード解説

このソースコードは、Pythonを使用して球面調和関数を計算し、3次元グラフとして可視化するものです。
以下はコードの章立て詳細な説明です。

ライブラリのインポート

• import numpy as np:
  数値計算用のライブラリであるNumPyをインポートします。
  npはNumPyの標準的な別名です。
• import matplotlib.pyplot as plt:
  グラフ描画用のライブラリであるMatplotlibのpyplotモジュールをインポートします。
  pltは一般的な別名です。
• from mpl_toolkits.mplot3d import Axes3D:
  3次元グラフ描画用のモジュールをインポートします。
• from scipy.special import sph_harm:
  SciPyライブラリの特殊関数モジュールから、球面調和関数をインポートします。

パラメータの設定

• theta = np.linspace(0, np.pi, 100):
  $0$から$π$の範囲を$100$個の等間隔で分割した配列を生成し、$θ$の値として設定します。
  ここで、$θ$は極角です。
• phi = np.linspace(0, 2 * np.pi, 100):
  $ 0$から$2π$の範囲を$100$個の等間隔で分割した配列を生成し、$φ$の値として設定します。
  ここで、$φ$は方位角です。
• theta, phi = np.meshgrid(theta, phi):
  thetaとphiの配列から格子状の座標を生成します。

球面調和関数の計算

• l = 3:
  球面調和関数の次数（degree）を$3$に設定します。
• m = 2:
  球面調和関数のオーダー（order）を$2$に設定します。
• Y_lm = sph_harm(m, l, phi, theta).real:
  sph_harm関数を使用して球面調和関数を計算します。
  .real属性を使用して実部を取得します。

球面座標から直交座標への変換

• x = Y_lm * np.sin(theta) * np.cos(phi):

球面座標系から直交座標系への変換を行います。

• y = Y_lm * np.sin(theta) * np.sin(phi):
  同様に、$y$座標を計算します。
• z = Y_lm * np.cos(theta):
  同様に、$z$座標を計算します。

グラフのプロット

• fig = plt.figure():
  新しい図を作成します。
• ax = fig.add_subplot(111, projection='3d'):
  3次元のサブプロットを追加します。
• ax.plot_surface(x, y, z, cmap='viridis'):

球面調和関数の結果を表す3次元曲面をプロットします。

グラフの装飾

• ax.set_title(f"Spherical Harmonic (l={l}, m={m})"): グラフのタイトルを設定します。
  使用された球面調和関数の次数とオーダーが表示されます。
• ax.set_xlabel('X'):
  $x$軸のラベルを設定します。
• ax.set_ylabel('Y'):
  $y$軸のラベルを設定します。
• ax.set_zlabel('Z'):
  $z$軸のラベルを設定します。

グラフの表示

• plt.show(): グラフを表示します。

これにより、球面調和関数の3次元グラフが生成され、その特性が視覚化されます。

結果解説

[実行結果]

このPythonコードによって生成されるグラフは、球面調和関数の特定のモード（$l$および$m$の値によって決まる）を可視化します。
以下はグラフの詳細な説明です。

1. グラフの形状:

• グラフは3次元の球面で表現されます。
  球面の各点には、球面調和関数の値に応じて高さが割り当てられます。
• 球面の外側は色で示され、色の濃淡は球面調和関数の値を表します。
  濃い部分は正の値を示し、薄い部分は負の値を示します。
• グラフの中央付近が高いピークを持つことがあります。
  このピークは球面調和関数の特性によるもので、球面の中心における極小値または極大値を表します。

2. 軸と座標系:

• グラフは3次元座標系で表示されます。
  $x$軸、$y$軸、$z$軸があり、それぞれが直交座標系の座標を表します。
• $x$軸と$y$軸は平面上にあり、球面上の点の位置を決定します。
  z軸は高さを表します。

3. グラフのタイトル:

• グラフのタイトルには、使用された球面調和関数のパラメータが含まれます。
  例えば、”Spherical Harmonic ($l=3$, $m=2$)” のような形式です。
• “l” は球面調和関数の次数を示し、球面の形状に影響を与えます。
• “m” は球面調和関数のオーダーを示し、球面の回転対称性に関連しています。

このように、グラフは球面上の特定のモードに関連付けられた球面調和関数の振る舞いを視覚的に表現します。

フォッカー-プランク方程式

フォッカー-プランク方程式は、確率過程の時間発展を記述する偏微分方程式です。

例えば、ブラウン運動などの確率過程の確率密度関数の時間変化を記述します。

1次元のフォッカー-プランク方程式は以下のように表されます。

$$
∂P(x,t)/∂t = -∂/∂x[D(1)(x,t)P(x,t)] + (1/2)∂^2/∂x^2[D(2)(x,t)P(x,t)]
$$

ここで、$P(x,t)$は確率密度関数、$D(1)(x,t)$は漂流係数、$D(2)(x,t)$は拡散係数です。

この方程式をPythonで解くには、数値計算が必要になります。
ここでは、有限差分法を使って近似的に解きます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

# 定数
D1 = 0.1  # 漂流係数
D2 = 0.01  # 拡散係数
X_MAX = 10.0  # x範囲
T_MAX = 10.0  # 時間範囲
N_X = 100  # x方向の分割数
N_T = 1000  # 時間ステップ数

# 配列の初期化
dx = X_MAX / (N_X - 1)
dt = T_MAX / (N_T - 1)
x = np.linspace(0, X_MAX, N_X)
t = np.linspace(0, T_MAX, N_T)
P = np.zeros((N_T, N_X))

# 初期条件
P[0] = np.exp(-(x - 3)**2 / 0.5)  # ガウス分布

# フォッカー-プランク方程式の解法
for i in range(N_T - 1):
    for j in range(1, N_X - 1):
        P[i+1, j] = P[i, j] \
                    - dt * (D1 * (P[i, j+1] - P[i, j-1]) / (2 * dx)) \
                    + (D2 * dt / (2 * dx**2)) * (P[i, j+1] - 2 * P[i, j] + P[i, j-1])
    P[i+1, 0] = P[i+1, 1]  # 端の条件
    P[i+1, -1] = P[i+1, -2]  # 端の条件

# 結果のプロット
fig, ax = plt.subplots(figsize=(8, 6))
for i in range(0, N_T, 100):
    ax.plot(x, P[i], label=f't = {t[i]:.2f}')
ax.set_xlabel('x')
ax.set_ylabel('P(x,t)')
ax.set_title('Fokker-Planck Equation')
ax.legend()
plt.show()

このコードでは、フォッカー-プランク方程式を有限差分法で近似的に解いています。
初期条件としてガウス分布を与え、時間発展させています。

出力される図は、確率密度関数$P(x,t)$の時間変化を示しています。
時間が経つにつれて、分布が拡散していく様子が確認できます。

[実行結果]

ソースコード解説

ここでは、フォッカー-プランク方程式の数値解を計算し、その結果を可視化するPythonコードについて説明します。

1. ライブラリのインポートと設定

1
2
3

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

NumPyとMatplotlibライブラリをインポートし、Matplotlibのインラインモードを有効にしています。

2. 定数の設定

1
2
3
4
5
6

D1 = 0.1  # 漂流係数
D2 = 0.01  # 拡散係数
X_MAX = 10.0  # x範囲
T_MAX = 10.0  # 時間範囲
N_X = 100  # x方向の分割数
N_T = 1000  # 時間ステップ数

フォッカー-プランク方程式の係数$(D1, D2)$、計算範囲$(X_MAX, T_MAX)$、空間と時間の分割数$(N_X, N_T)$を設定しています。

3. 配列の初期化

1
2
3
4
5

dx = X_MAX / (N_X - 1)
dt = T_MAX / (N_T - 1)
x = np.linspace(0, X_MAX, N_X)
t = np.linspace(0, T_MAX, N_T)
P = np.zeros((N_T, N_X))

空間と時間の刻み幅$(dx, dt)$、座標と時間の配列$(x, t)$、確率密度関数の配列$P(N_T x N_X)$を初期化しています。

4. 初期条件の設定

1

P[0] = np.exp(-(x - 3)**2 / 0.5)  # ガウス分布

初期の確率密度関数にガウス分布(平均値$3$、分散$0.5$)を設定しています。

5. フォッカー-プランク方程式の解法

1
2
3
4
5
6
7

for i in range(N_T - 1):
    for j in range(1, N_X - 1):
        P[i+1, j] = P[i, j] \
                    - dt * (D1 * (P[i, j+1] - P[i, j-1]) / (2 * dx)) \
                    + (D2 * dt / (2 * dx**2)) * (P[i, j+1] - 2 * P[i, j] + P[i, j-1])
    P[i+1, 0] = P[i+1, 1]  # 端の条件
    P[i+1, -1] = P[i+1, -2]  # 端の条件

フォッカー-プランク方程式を有限差分法で近似的に解いています。

時間ループとx方向のループを使って、各時間ステップと空間格子点における確率密度関数の値を計算しています。
また、端の条件も設定しています。

6. 結果のプロット

1
2
3
4
5
6
7
8

fig, ax = plt.subplots(figsize=(8, 6))
for i in range(0, N_T, 100):
    ax.plot(x, P[i], label=f't = {t[i]:.2f}')
ax.set_xlabel('x')
ax.set_ylabel('P(x,t)') 
ax.set_title('Fokker-Planck Equation')
ax.legend()
plt.show()

最後に、計算結果をプロットしています。
時間ステップごとに確率密度関数$P(x,t)$をプロットし、各曲線に対応する時刻tを凡例に表示しています。
また、軸ラベルとタイトルを設定し、グラフを表示しています。

このコードでは、フォッカー-プランク方程式の数値解を計算し、確率密度関数の時間発展を可視化しています。
初期条件にガウス分布を与え、時間の経過とともに確率密度がどのように拡散していくかを示しています。

結果解説

[実行結果]

出力されるグラフは、確率密度関数 $P(x,t)$の時間発展を示しています。

• 横軸は$x$で、確率変数の値を表します。
• 縦軸は$P(x,t)$で、その時刻$t$における確率密度を表します。

グラフには複数の曲線が描かれています。
それぞれの曲線は異なる時刻$t$における確率密度関数$P(x,t)$を表しています。

• 初期条件($t=0$)の曲線は、平均値が$3$、分散が$0.5$のガウス分布になっています。
• 時間が経つにつれ、曲線が広がっていく様子が見て取れます。
  これは確率密度関数が拡散していることを表しています。
• 端($x=0$および$x=X_MAX$)の条件を満たすため、曲線の両端は$0$に近づくように調整されています。

凡例には、各曲線に対応する時刻tが表示されています。
例えば、最初の曲線は$t=0.00$、次の曲線は$t=1.00$というように時間が経過しています。

このグラフから、次のような情報が読み取れます:

1. 初期の確率分布の形状
2. 時間の経過とともに確率分布がどのように変化するか
3. 確率密度がどのように拡散し、平らになっていくか
4. 端の条件がどのように満たされているか

フォッカー-プランク方程式は、このように確率過程の時間発展を記述する役割があり、このグラフはその数値解の可視化結果になっています。

ガウス-ボナールの微分方程式

ガウス-ボナールの微分方程式は、曲面の局所的な幾何学的性質を記述する重要な式です。

この式は以下のように表されます:

$$
k = K dA
$$

• $k$ は曲面上の任意の閉曲線の総曲率です。
• $K$ は曲面のガウス曲率です。
  ガウス曲率は、曲面上の点における内在的な曲がり具合を表します。
• $dA$ は閉曲線に囲まれた小さな領域の面積です。

つまり、ガウス-ボナールの式は、閉曲線の総曲率が、その曲線に囲まれた領域のガウス曲率に比例することを示しています。

この式は、位相幾何学の分野で非常に重要です。
特に、コンパクト(閉じた有界)な曲面のトポロジー(位相的な形状)は、その曲面のガウス曲率に関係しているためです。

具体的な応用例としては、一般相対性理論におけるアインシュタインの方程式の導出や、相対論的な宇宙モデルの研究などがあります。
また、コンピューターグラフィックスにおける曲面モデリングにも使われています。

このように、ガウス-ボナールの式は、曲面の局所的な性質とグローバルな性質を関連付ける重要な式なのです。

ソースコード

Pythonを使用してガウス-ボナール方程式を解き、その解をグラフ化する例を示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt

# ガウス-ボナールの微分方程式
def gauss_bonnet(u, v):
    k = 1  # カーブの曲率
    return k * np.sqrt(1 + u**2 + v**2)

# パラメータの範囲
u = np.linspace(-2, 2, 50)
v = np.linspace(-2, 2, 50)
U, V = np.meshgrid(u, v)

# 数値解の計算
Z = gauss_bonnet(U, V)

# グラフの描画
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(U, V, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('u')
ax.set_ylabel('v')
ax.set_zlabel('z')
ax.set_title('Gauss-Bonnet Equation')
plt.show()

このコードは以下の手順で動作します。

1. NumPyとMatplotlibをインポートし、3D描画用のモジュールをインポートします。
2. ガウス-ボナールの微分方程式を定義した関数gauss_bonnetを作成します。
   この関数は、曲率kと変数u、vを引数にとり、微分方程式の解を返します。
3. パラメータuとvの範囲をnp.linspace関数を使って設定します。
4. np.meshgrid関数を使って、uとvの全ての組み合わせを計算します。
5. gauss_bonnet関数を使って、微分方程式の数値解Zを計算します。
6. Matplotlibを使って3D図を作成し、plot_surface関数で数値解の曲面を描画します。
7. 軸ラベルとタイトルを設定します。
8. plt.show()で、グラフを表示します。

このコードを実行すると、ガウス-ボナールの微分方程式の数値解が3D曲面として描画されます。
変数uとvの値によって、曲面の形状が変化することがわかります。

[実行結果]

注意点として、このコードではガウス-ボナールの微分方程式の特定の解のみを可視化しています。
実際の微分方程式の解は、初期条件や境界条件によって異なります。
より一般的な解を可視化するには、微分方程式の数値解法を適用する必要があります。

結果解説

[実行結果]

この3D曲面グラフには、いくつかの重要な特徴があります。

詳しく説明しましょう。

1. 曲面の形状

• この曲面は、ガウス-ボナールの微分方程式の数値解を表しています。
• 曲面の形状は、変数uとvの値によって変化します。
• 中心付近では平らな形状ですが、外側に向かうにつれて曲率が大きくなり、山のような形状になります。

2. 曲面の色

• 曲面の色は、カラーマップviridisを使って割り当てられています。
• 青から緑、黄色、オレンジ、赤と変化し、高さ(zの値)が大きいほど赤に近い色になります。
• 色の変化によって、曲面の高低差が視覚的に分かりやすくなります。

3. 軸とラベル

• x軸は変数u、y軸は変数v、z軸は微分方程式の解zを表しています。
• 各軸にはラベル(‘u’、’v’、’z’)が付けられています。

4. タイトル

• グラフのタイトルは’Gauss-Bonnet Equation’となっています。

5. プロットの詳細

• rstride=1, cstride=1のオプションにより、曲面のメッシュ解像度が最大になっています。
• つまり、すべてのデータ点が曲面にプロットされ、滑らかな表面が得られます。

このように、生成されるグラフは、ガウス-ボナールの微分方程式の数値解の3D表現を視覚化したものです。

変数の値によって曲面の形状が変化し、色分けによって高低差が分かりやすくなっています。

軸ラベルとタイトルも付加されているため、グラフの解釈がしやすくなっています。