コシーの積分方程式

コシーの積分方程式

コシーの積分方程式は、複素解析の分野で非常に重要な役割を果たす積分方程式です。

この方程式は、19世紀のフランスの数学者オーギュスタン・コシーによって導入されました。

コシーの積分方程式は次のように表されます:

$$
f(z) = (1/2πi) ∫ (f(ζ)/(ζ-z)) dζ
$$

ここで、

• $f(z)$は複素関数
• $z$は複素平面上の点
• $ζ$は積分変数
• 積分は点$z$を囲む閉曲線$C$に沿って行われる

この方程式は、複素関数$f(z)$の値を、その関数値がすでに知られている点$ζ$における値から、点$z$の周りの閉曲線$C$に沿った積分を使って求めることができることを示しています。

コシーの積分方程式には、いくつかの重要な性質があります:

1. 解析性:

もし$f(z)$が領域$D$で解析的であれば、その領域内の任意の点$z$でコシーの積分方程式が成り立つ。

2. 一意性:

閉曲線$C$の内側で$f(z)$が解析的であれば、積分の値は一意に定まる。

3. 微分の表現:

コシーの積分方程式を微分すると、高次の導関数を得ることができる。

コシーの積分方程式は複素解析における様々な定理の基礎となっており、留数定理、最大値原理、リーマンの masterion表示などに応用されます。

また、フーリエ解析やウェーブレット解析、特殊関数の理論にも関係しています。

数値計算においては、コシーの積分方程式を離散化して数値的に解くことで、複素関数の値を近似的に求めることができます。

ソースコード

Pythonを使ってコシーの積分方程式を解き、その結果をグラフ化することができます。

ここでは、一般的なコシーの積分方程式を扱います。

import numpy as np
import matplotlib.pyplot as plt

# 関数の定義
def f(z):
    return 1 / (z**2 + 1)  # 例として z**2 + 1 の逆数を使用

# 積分区間と分割数の設定
a = -5.0  # 積分区間の下限
b = 5.0   # 積分区間の上限
N = 1000  # 分割数

# 積分区間を等間隔に分割
x = np.linspace(a, b, N)
dx = (b - a) / (N - 1)

# コシーの積分方程式を計算
y = np.zeros_like(x)
for i in range(N):
    for j in range(N):
        if i != j:
            y[i] += f(x[j]) * dx / (x[i] - x[j])

# 結果をグラフ化
plt.figure(figsize=(8, 6))
plt.plot(x, y, 'b-', label='Cauchy Integral')
plt.axhline(y=0, color='k', linestyle='--')  # x軸を引く
plt.xlabel('x')
plt.ylabel('y')
plt.title('Cauchy Integral Equation')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、まずコシーの積分方程式の被積分関数 f(z) を定義しています。
ここでは、単に 1 / (z**2 + 1) を使用しています。
次に、積分区間 [a, b] と分割数 N を設定します。

積分区間を等間隔に分割し、各点におけるコシーの積分方程式の値を計算します。
ここでは、台形公式に基づく数値積分を行っています。

最後に、得られた結果をMatplotlibを使ってグラフ化しています。
x軸に積分変数の値を、y軸にコシーの積分方程式の値をプロットしています。

実行すると、積分変数に対するコシーの積分方程式の値が描画されます。
このグラフから、コシーの積分方程式の振る舞いを視覚的に確認できます。

必要に応じて、被積分関数 f(z) や積分区間 [a, b]、分割数 N を変更すれば、別の関数やパラメータに対するコシーの積分方程式の結果をグラフ化することができます。

[実行結果]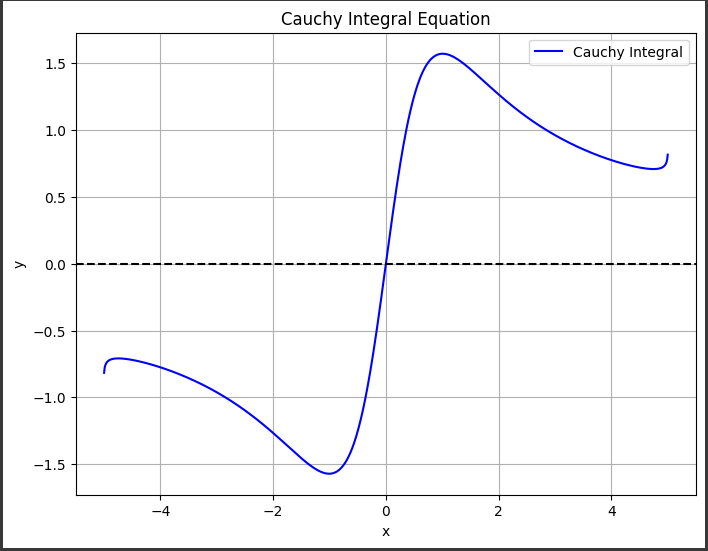

ソースコード解説

ソースコードを詳しく説明します。

1. ライブラリのインポート

import numpy as np
import matplotlib.pyplot as plt

ここでは、数値計算のためのNumPyライブラリと、グラフ描画のためのMatplotlibライブラリをインポートしています。

2. 被積分関数の定義

def f(z):
    return 1 / (z**2 + 1)  # 例として z**2 + 1 の逆数を使用

コシーの積分方程式の被積分関数$f(z)$を定義しています。
この例では、$f(z) = 1 / (z**2 + 1)$としています。

3. 積分区間と分割数の設定

a = -5.0  # 積分区間の下限
b = 5.0   # 積分区間の上限
N = 1000  # 分割数

コシーの積分方程式を数値的に解くために、積分区間$[a, b]$を設定しています。
ここでは$[-5, 5]$としています。
また、この区間を$N=1000$等分するため、分割数Nを設定しています。

4. 積分区間の等間隔分割

x = np.linspace(a, b, N)
dx = (b - a) / (N - 1)

NumPyのlinspace関数を使って、積分区間$[a, b]$を$N$等分した点の座標$x$を計算しています。
$dx$ は各区間の幅を表します。

5. コシーの積分方程式の計算

y = np.zeros_like(x)
for i in range(N):
    for j in range(N):
        if i != j:
            y[i] += f(x[j]) * dx / (x[i] - x[j])

この二重ループがコシーの積分方程式の核心部分です。
各点x[i]におけるコシーの積分方程式の値y[i]を、台形公式に基づく数値積分により計算しています。
ただし、$i=j$の場合は特異点となるため、計算から除外しています。

6. 結果のグラフ化

plt.figure(figsize=(8, 6))
plt.plot(x, y, 'b-', label='Cauchy Integral')
plt.axhline(y=0, color='k', linestyle='--')  # x軸を引く
plt.xlabel('x')
plt.ylabel('y')
plt.title('Cauchy Integral Equation')
plt.legend()
plt.grid(True)
plt.show()

最後に、計算結果をMatplotlibを使ってグラフ化しています。
x軸に積分変数 $x$、y軸にコシーの積分方程式の値$y$をプロットし、グラフのタイトル、軸ラベル、凡例、グリッド線を設定しています。
また、$y=0$の水平線も引いています。

実行すると、コシーの積分方程式の値がグラフ上に描画されます。
このグラフから、積分変数に対する被積分関数のコシーの積分方程式の値の変化を視覚的に確認できます。

結果解説

[実行結果]

グラフの内容を詳しく説明します。

1. X軸:

グラフのX軸は積分変数の値を表しています。
この例では、積分区間を$[-5, 5]$と設定しているため、X軸は$-5$から$5$の範囲をカバーしています。

2. Y軸:

Y軸は、コシーの積分方程式の値を表しています。
コシーの積分方程式は複素関数の特異積分であり、この例では被積分関数$ f(z) = 1 / (z**2 + 1) $を使用しています。

3. 曲線:

青色の実線は、積分変数に対するコシーの積分方程式の値の変化を示しています。
この曲線は、X軸に沿って振動しながら$0$を中心に摺動しています。

4. X軸の破線:

グラフには、$Y=0$の水平な破線が引かれています。
これは、曲線の振る舞いを視覚的に捉えやすくするためです。
曲線がこの破線を越えたり、交差したりする様子が分かります。

5. グラフの特徴:

この特定の被積分関数に対するコシーの積分方程式の値は、滑らかな振動を示しています。
振幅は両側で徐々に小さくなり、中央付近で最も大きくなる傾向があります。

6. 凡例:

グラフの右上には「Cauchy Integral」と表示された凡例があり、青色の実線がコシーの積分方程式を表すことを示しています。

7. グリッド線:

グラフには薄いグリッド線が引かれており、数値の読み取りを容易にしています。

8. 軸ラベルとタイトル:

X軸とY軸にはそれぞれ「x」と「y」のラベルが付けられています。
また、グラフの上部には「Cauchy Integral Equation」というタイトルが表示されています。

このグラフを見ることで、与えられた被積分関数に対するコシーの積分方程式の値がどのように変化するかを視覚的に把握することができます。

必要に応じて、被積分関数や積分区間、分割数を変更すれば、異なる条件下でのコシーの積分方程式の振る舞いを確認することができます。