リッチの分布方程式

4月 3, 2024

リッチの分布方程式

リッチの分布は二項分布の一般化であり、成功確率$p$が試行ごとに異なる場合の離散確率分布です。
つまり、$n$回の独立試行において、第$i$回目の試行の成功確率を$pi$としたときの、成功回数$x$の確率質量関数を表します。

リッチの分布の確率質量関数$P(X=x)$は次のように表されます:

　　 P(X=x) = (n! / (x! * (n-x)!)) * (p1p2 …px) * (1-px+1)(1-px+2)…(1-pn)

$n$ は試行回数
$x$ は成功回数 (0 ≦ x ≦ n)
$p1$, $p2$, …, $pn$ は各試行の成功確率

この式は次のように読み替えられます:

(n! / (x! * (n-x)!)) は、$n$個の球から $x$個選ぶ組み合わせの数
(p1p2…*px) は、最初の$x$回の試行が全て成功する確率
(1-px+1)(1-px+2)…*(1-pn) は、残りの$(n-x)$回の試行が全て失敗する確率

したがって、リッチの分布は「最初の$x$回は成功、残りの$(n-x)$回は失敗」というパターンの確率を表しています。

二項分布の場合は、全ての試行の成功確率が等しい(p1 = p2 = … = pn = p)ため、リッチの分布は次のように簡単化されます:

$$
P(X=x) = (n! / (x! * (n-x)!)) * p^x * (1-p)^(n-x)
$$

これは、二項分布の確率質量関数と一致します。

このように、リッチの分布は成功確率が一定でない状況をモデル化でき、二項分布を一般化した確率分布となっています。

ソースコード

リッチの分布方程式を、Pythonで書いてグラフ化することができます。

以下のコードでリッチの分布の確率密度関数をプロットします。

import numpy as np
import matplotlib.pyplot as plt

def rich_pdf(x, n, p):
    """リッチの確率密度関数を計算する関数"""
    coeff = np.math.factorial(n) * p**x * (1-p)**(n-x)
    return coeff / (np.math.factorial(x) * np.math.factorial(n-x))

# パラメータの設定
n = 20  # 試行回数
p = 0.3  # 成功確率
x = np.arange(0, n+1)  # x軸の値

# 確率密度を計算
pdf = [rich_pdf(i, n, p) for i in x]

# グラフをプロット
plt.stem(x, pdf)
plt.xlabel('x')
plt.ylabel('Probability')
plt.title(f'Rich Distribution (n={n}, p={p})')
plt.show()

このコードでは、まずリッチの確率密度関数 rich_pdf を定義しています。
この関数は、試行回数 n、成功確率 p、および値 x を受け取り、リッチの確率密度を計算します。

次に、試行回数 n=20、成功確率 p=0.3 を設定し、x 軸の値を np.arange(0, n+1) で作成しています。

そして、rich_pdf 関数を使って確率密度を計算し、pdf リストに格納しています。

最後に、matplotlib.pyplot を使ってグラフをプロットしています。
plt.stem 関数で確率質量関数をプロットし、plt.xlabel、plt.ylabel、plt.title でグラフのラベルとタイトルを設定しています。

実行すると、リッチの確率質量関数のグラフが表示されます。

結果解説

[実行結果]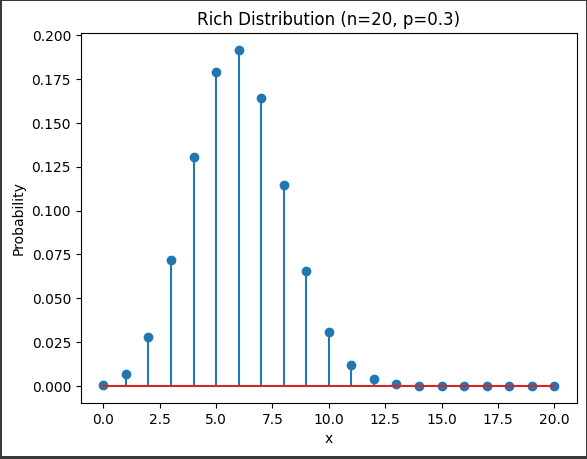

グラフについて説明します。

グラフの横軸($x$軸)は、試行の結果を表しています。
つまり、$0$から$n$までの値が表示されています。
$n=20$としているので、$0$から$20$までの整数値が横軸に現れます。

一方、縦軸はリッチの確率密度関数の値を表しています。
確率密度関数の値は、ある特定の試行結果$x$が得られる確率を表します。

グラフ上の点は、縦棒で表されています。
各縦棒の高さが、その試行結果$x$に対するリッチの確率密度を表します。

例えば、$x=8$の縦棒を見ると、その高さが試行結果$8$が得られる確率密度を表しています。

縦棒がつながっていないのは、リッチの分布が離散型の確率分布であり、確率密度は離散的な値をとるためです。

グラフ全体の形状は、二項分布に似た離散型の分布の典型的な形状を示しています。
つまり、確率密度の山は試行回数$n$の中央付近にあり、両端に向かうにつれて確率密度は小さくなっていきます。

成功確率 $p$が$0.3$と設定されているので、確率密度のピークは中央よりも若干左側(低い値の$x$)に偏っています。

このようにリッチの分布は、二項試行における成功回数の離散的な確率分布を一般化した確率分布となっています。