シュワルツの不等式

シュワルツの不等式

シュワルツの不等式とは、2つのベクトルの内積の絶対値の2乗は、それぞれのベクトルのノルム(長さ)の積以下であるということを示す不等式です。

つまり、ベクトル$a = (a1, a2, …, an)$、ベクトル$b = (b1, b2, …, bn)$に対して、

$ (a1 * b1 + a2 * b2 + … + an * bn)^2 ≦ (a1^2 + a2^2 + … + an^2) * (b1^2 + b2^2 + … + bn^2) $

が成り立ちます。

左辺はベクトル$a$・$b$の内積の絶対値の2乗、右辺は $a$のノルムと$b$のノルムの積を表しています。

この不等式は、ベクトル内積が最大になるのは、2つのベクトルが同じ方向を向いている時であり、ベクトル間の角度が大きくなるほど内積は小さくなることを意味しています。

幾何学的には、2つのベクトルを組み合わせて作った平行四辺形の面積は、底辺と高さの積以下であることを表しています。

このようにシュワルツの不等式は、ベクトルの内積とノルムの関係を不等式の形で表した重要な結果となっています。

サンプルコード

シュワルツの不等式は、以下の式で表されます。

$$
(x^2 + y^2) * (1 + x^2 + y^2) >= 1
$$

この不等式は、2変数 x と y の関数として表すことができます。

次のコードでは、シュワルツの不等式を3D空間上に可視化しています。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# シュワルツの不等式を表す関数
def f(x, y):
    return (x**2 + y**2) * (1 + x**2 + y**2)

# グラフ化する範囲
x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)

# グラフを描画
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('Schwarz Inequality Visualization')

plt.show()

まず、f(x, y) 関数でシュワルツの不等式の右辺を定義しています。

次に、x と y の値の範囲を設定しています。
ここでは、xとyがそれぞれ -2 から 2 までの範囲を 100 分割して計算しています。
np.meshgrid関数を使うことで、XとYの格子点上の値を求めています。

Z = f(X, Y) では、XとYの格子点上での関数値を計算しています。

最後に、matplotlibとmpl_toolkits.mplot3dを使って、X、Y、Zの値から3D曲面を描画しています。
plot_surface関数を使うことで、格子点上の値から滑らかな曲面を描くことができます。
cmap='viridis'は、曲面の色付けに使われるカラーマップを指定しています。

実行すると、x、y、z軸に対して、シュワルツの不等式の右辺を表す3D曲面が描画されます。
この曲面の形状から、不等式の性質を視覚的に確認することができます。

このように、任意の$2$変数関数を指定して、その関数値を3D空間上に可視化することができます。

[実行結果]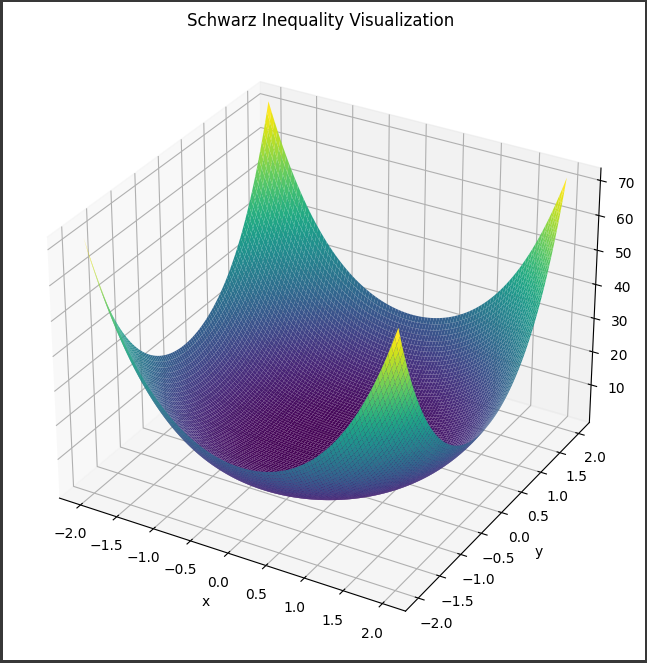

ソースコード解説

ソースコードの詳細を説明します。

1. モジュールのインポート:

1
2
3
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  • numpy：数値計算ライブラリで、配列や行列演算を効率的に処理します。
  • matplotlib.pyplot：グラフ描画ライブラリで、グラフや図形を描画します。
  • mpl_toolkits.mplot3d：3次元グラフ描画のためのモジュールです。

2. 関数の定義:

1
2
def f(x, y):
    return (x**2 + y**2) * (1 + x**2 + y**2)
  • f(x, y) 関数は、2つの引数 x と y を受け取り、シュワルツの不等式を表す関数です。
    式 (x**2 + y**2) * (1 + x**2 + y**2) を計算して結果を返します。

3. グラフ化する範囲の設定:

1
2
3
4
x = np.linspace(-2, 2, 100)
y = np.linspace(-2, 2, 100)
X, Y = np.meshgrid(x, y)
Z = f(X, Y)
  • np.linspace(-2, 2, 100) によって、範囲$ ([-2, 2]) $を$100$個の等間隔に区切った数列を生成し、x と y に代入します。
  • np.meshgrid(x, y) によって、x と y のすべての組み合わせに対する格子状の座標行列 X と Y を生成します。
  • f(X, Y) によって、X と Y の各座標における関数 f(x, y) の値を計算し、Z に格納します。

4. グラフの描画:

1
2
3
4
5
6
7
8
9
10
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title('Schwarz Inequality Visualization')

plt.show()
  • plt.figure(figsize=(10, 8)) によって、図のサイズを設定します。
  • fig.add_subplot(111, projection='3d') によって、3Dグラフを描画するためのサブプロットを追加します。
  • ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis') によって、3D 曲面を描画します。
    rstride と cstride はメッシュの密度を制御するパラメータです。
  • ax.set_xlabel('x')、ax.set_ylabel('y')、ax.set_zlabel('z') によって、各軸のラベルを設定します。
  • ax.set_title('Schwarz Inequality Visualization') によって、図のタイトルを設定します。
  • plt.show() によって、描画したグラフを表示します。

結果解説

[実行結果]

出力される3D曲面は、シュワルツの不等式 $(x^2 + y^2) * (1 + x^2 + y^2) >= 1 $の右辺の値を、$x-y$平面上の点$(x, y)$について表しています。
カラーマップの濃い色ほど、不等式の右辺の値が大きくなっています。

この曲面の形状から、不等式の性質を視覚的に確認できます。
例えば、原点$(0, 0)$周辺では不等式の両辺が等しくなり、原点から離れるほど右辺の値が大きくなっていきます。
また、曲面は原点を中心として点対称の形状をしており、不等式の性質である「$x^2 + y^2 >= 0$」も確認できます。

このグラフを見ることで、シュワルツの不等式の形状的な特徴や、成り立つ範囲などを直感的に把握することができます。