ディリクレ問題
ディリクレ問題は、偏微分方程式の境界値問題の一種です。
この問題では、以下の3つの要素が与えられます。
1. 偏微分方程式
- 通常は、ラプラス方程式やポアソン方程式などの楕円型偏微分方程式が扱われます。
2. 領域($Ω$)
- 問題が定義される有界な領域です。
例えば、矩形、円、三角形などの2次元または3次元の領域です。
3. 境界条件
- 領域の境界 ($∂Ω$)上で、未知関数の値が与えられた関数$(f)$に等しくなるという条件です。
ディリクレ問題では、与えられた偏微分方程式と境界条件のもとで、領域内の未知関数 $u(x,y)$の値を求める必要があります。
つまり、領域内部の解を求めることが目的です。
この問題は、数学的にはよく研究されており、様々な解法が知られています。
代表的な解法としては、離散化による数値解法、有限要素法、分離変数法、グリーン関数法などがあります。
ディリクレ問題の応用例としては、電位問題、伝導問題、膜の振動問題、量子力学などがあげられます。
工学や物理学の分野で重要な役割を果たしています。
ソースコード
ディリクレ問題をPythonで解いて、グラフ化します。
ディリクレ問題は、偏微分方程式の境界値問題の一つです。
2次元の場合、方程式は以下のように記述されます。
$$
∂^2u/∂x^2 + ∂^2u/∂y^2 = 0 (on Ω)
$$
$$
u = f(x, y) (on ∂Ω)
$$
- $u(x, y) $は未知関数
- $Ω $は領域
- $∂Ω $は$Ω$の境界
- $f(x, y) $は与えられた境界条件
Pythonコードは以下の通りです。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import dblquad
x_min, x_max = 0, 1
y_min, y_max = 0, 1
def boundary(x, y):
return np.sin(np.pi * x) * np.sinh(np.pi * y)
def dirichlet_solution(x, y):
return np.sin(np.pi * x) * np.sinh(np.pi * y) / np.sinh(np.pi)
def integrate(f, x_min, x_max, y_min, y_max):
return dblquad(f, x_min, x_max, lambda x: y_min, lambda x: y_max)[0]
x = np.linspace(x_min, x_max, 50)
y = np.linspace(y_min, y_max, 50)
X, Y = np.meshgrid(x, y)
Z = dirichlet_solution(X, Y)
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('U(x, y)')
ax.set_title('Dirichlet Problem Solution')
plt.show()
|
このコードでは、最初に領域とその境界条件を定義しています。
境界条件は boundary 関数で与えられています。
次に、ディリクレ問題の解析的な解 dirichlet_solution を定義しています。
この関数は、与えられた境界条件のもとで、ディリクレ問題の解を返します。
integrate 関数は、数値積分を行うための関数です。
ここでは使用していませんが、必要に応じて利用できます。
次に、グリッド点での解の値を計算しています。
np.meshgrid を使って、$X$, $Y$, $Z$ の値を計算しています。
最後に、matplotlib の plot_surface を使って、3D プロットを作成しています。
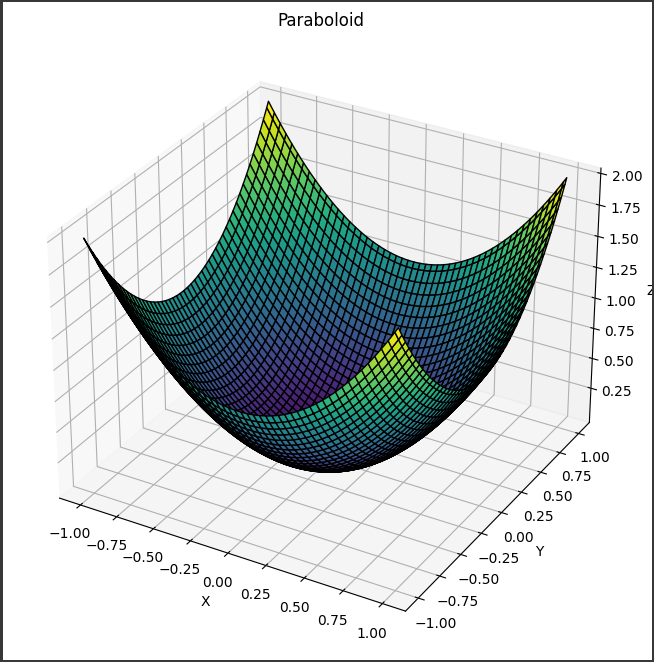
実行すると、以下のような3Dグラフが表示されます。
[実行結果]
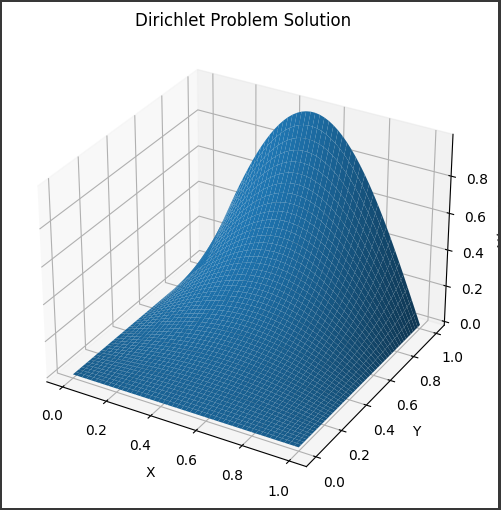
このグラフは、与えられた境界条件のもとでのディリクレ問題の解を視覚化したものです。
境界条件に応じて、解の形状が変化します。
ソースコード解説
ソースコードを説明します。
1. ライブラリのインポート
1
2
3
| import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import dblquad
|
このセクションでは、数値計算や可視化に使用するライブラリ(NumPy, Matplotlib, SciPy)をインポートしています。
2. 問題設定
1
2
3
4
5
6
7
|
x_min, x_max = 0, 1
y_min, y_max = 0, 1
def boundary(x, y):
return np.sin(np.pi * x) * np.sinh(np.pi * y)
|
ここでは、ディリクレ問題の領域$([0, 1] x [0, 1])$と、境界上での条件を定義しています。
boundary関数は、境界上での未知関数の値を返します。
3. 解析解の定義
1
2
3
|
def dirichlet_solution(x, y):
return np.sin(np.pi * x) * np.sinh(np.pi * y) / np.sinh(np.pi)
|
この関数は、与えられた境界条件のもとでのディリクレ問題の解析解を返します。
つまり、この解が領域内部で満たすべき関数形です。
4. 数値積分関数の定義
1
2
3
|
def integrate(f, x_min, x_max, y_min, y_max):
return dblquad(f, x_min, x_max, lambda x: y_min, lambda x: y_max)[0]
|
この関数は、2重積分を数値的に計算するためのものです。
ここでは使用していませんが、必要に応じて利用できます。
5. グリッド点での解の値の計算
1
2
3
4
5
|
x = np.linspace(x_min, x_max, 50)
y = np.linspace(y_min, y_max, 50)
X, Y = np.meshgrid(x, y)
Z = dirichlet_solution(X, Y)
|
このセクションでは、領域内のグリッド点での解の値を計算しています。
np.linspaceを使って$x、y$の座標値を生成し、np.meshgridでそれらの組み合わせを作成しています。
最後に、dirichlet_solution関数を使って各グリッド点での解の値$Z$を計算しています。
6. 3D可視化
1
2
3
4
5
6
7
8
9
|
fig = plt.figure(figsize=(10, 6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('U(x, y)')
ax.set_title('Dirichlet Problem Solution')
plt.show()
|
最後のセクションでは、計算した解の値$Z$を3D曲面プロットで可視化しています。
matplotlib.pyplot.figureでフィギュアを作成し、add_subplotでプロット領域を追加しています。
plot_surfaceを使って$X$、$Y$、$Z$の値から曲面を描画しています。
最後に、軸ラベルとタイトルを設定し、show()でグラフを表示しています。
このコードは、与えられた境界条件のもとでのディリクレ問題の解析解を計算し、3D曲面グラフで可視化しています。
このようにして、解の振る舞いを視覚的に確認することができます。
結果解説
[実行結果]

グラフに表示されている内容を説明します。
1. グラフの種類
- このグラフは3次元の曲面グラフで、
matplotlib の plot_surface 関数を使って作成されています。
2. 軸の説明
- X軸: これは領域の$x$座標を表しています。
領域は$ [0, 1] $の範囲です。
- Y軸: これは領域の$y$座標を表しています。
領域は$ [0, 1] $の範囲です。
- Z軸: これは未知関数 $u(x, y)$の値を表しています。
3. 曲面の形状
- この曲面は、与えられた境界条件の下でのディリクレ問題の解析解を表しています。
- 具体的には、境界条件
u(x, y) = sin(πx) * sinh(πy) のもとで、解は u(x, y) = sin(πx) * sinh(πy) / sinh(π) となります。
- 曲面の形状は、この解析解の式に従って決まります。
4. 境界の値
- この曲面は、$x=0$, $x=1$, $y=0$, $y=1$ の境界上で、与えられた境界条件の値をとります。
- つまり、曲面の$4$辺は境界条件の値に一致しています。
5. 曲面の振る舞い
- $x$方向と$y$方向で、曲面は周期的な振る舞いを示します。
これは境界条件の三角関数とひ過関数の影響です。
- 中心付近ではほぼ平坦ですが、境界に近づくにつれて値が大きくなります。
このように、このグラフはディリクレ問題の解析解の形状を視覚的に表現しています。
与えられた境界条件の下で、解がどのような振る舞いを示すかがわかります。
境界値問題の解を理解する上で、このようなグラフは非常に有用です。