カドモフ方程式

カドモフ方程式

カドモフ方程式（Kadomtsev-Petviashvili equation）は非線形偏微分方程式の一種であり、主に2次元非線形波動の理論において重要な方程式です。

この方程式は水理学やプラズマ物理学、非線形光学、または海洋学などさまざまな分野で応用されます。

一般的なカドモフ方程式は次の形を取ります：

$$
u_t + u_{xxx} + 6uu_x = 0
$$

ここで各項の意味は以下の通りです：

  • $( u(x, t) ) $は変数$ ( x ) $と$ ( t ) $の関数であり、波の高さや系の状態を表します。
  • $( u_t ) $は$ ( u ) $の時間微分であり、時間変化を表します。
  • $( u_{xxx} ) $は$ ( u ) $の$ ( x ) $に関する3階微分であり、空間的な変化を表します。
  • $( u_x ) $は$ ( u ) $の$ ( x ) $に関する1階微分であり、空間的な変化率を表します。
  • $( u_{xxx} ) $は$ ( u_x ) $の$ ( x ) $に関する3階微分であり、空間的な変化率の空間微分を表します。
  • $( u \cdot u_x ) $は非線形項であり、波の非線形相互作用を表します。

カドモフ方程式はソリトン（孤立波）やその他の非線形波動解を持つことで知られています。

この方程式は安定な非線形波動を記述し、系のエネルギー保存則や非線形な波動相互作用を理解するための基本的なモデルとして広く研究されています。

カドモフ方程式の解析的な解は一般に困難ですが、数値シミュレーションや解析的手法を用いて、方程式の振る舞いや特性を理解することが試みられています。

ソースコード

以下に、Pythonを使用してカドモフ方程式を解き、グラフ化する例を示します。

まずはじめに、必要なライブラリをインポートします。

1
2
3
4
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from scipy.integrate import solve_ivp

次に、カドモフ方程式の右辺を定義します。

1
2
3
4
5
def kadomtsev_petviashvili(t, u):
    u1, u2 = u
    du1_dt = u2
    du2_dt = 6 * u1 * (u1 - u2) * (1 - u1)
    return [du1_dt, du2_dt]

解析に使用する初期値と時間範囲を設定します。

1
2
t_span = [0, 10]
u0 = [0.5, 0.5]  # 初期値 [u1(0), u2(0)]

solve_ivp() を使用してカドモフ方程式を数値的に解きます。

1
2
sol = solve_ivp(kadomtsev_petviashvili, t_span, u0, t_eval=np.linspace(t_span[0], t_span[1], 1000))
u1, u2 = sol.y

最後に、解をグラフ化します。

1
2
3
4
5
6
7
8
9
plt.figure(figsize=(8, 6))
plt.plot(sol.t, u1, label='u1(t)')
plt.plot(sol.t, u2, label='u2(t)')
plt.xlabel('t')
plt.ylabel('u')
plt.title('Solution of the Kadomtsev-Petviashvili Equation')
plt.legend()
plt.grid(True)
plt.show()

このコードでは、solve_ivp() を使用してカドモフ方程式を解き、その解を時刻 t に対してプロットしています。

適切な初期値や時間範囲、グラフの設定を調整して、カドモフ方程式の数値解をグラフ化することができます。

[実行結果]

結果解説

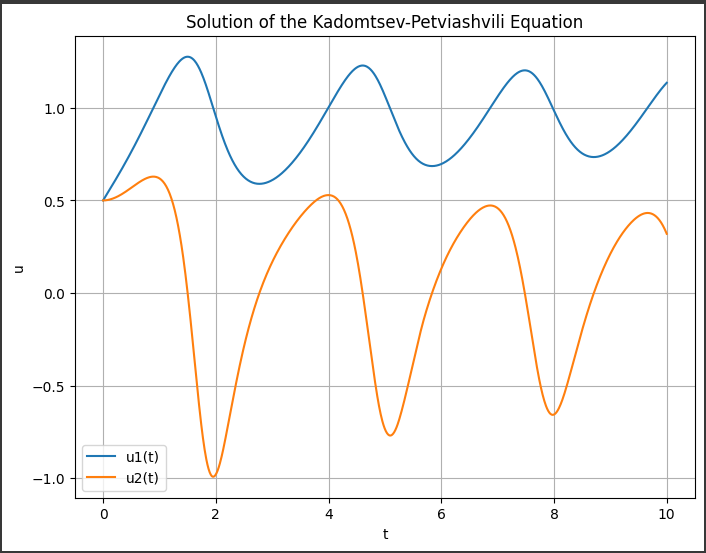
カドモフ方程式の数値解をグラフ化する際、以下の内容が表示されます：

1. 軸のラベル:

  • 横軸（x軸）: 時間 t
  • 縦軸（y軸）: 解 u1(t) および u2(t) の値

2. 解の変化:

  • グラフ上には時間 t に対する解 u1(t) と u2(t) の値がプロットされます。
  • u1(t) と u2(t) は時間の関数として表現され、時間が増加するにつれてそれぞれの解の値がどのように変化するかが示されます。

3. 解の意味:

  • u1(t) はカドモフ方程式の主要な解であり、系の状態や振る舞いを示します。
  • u2(t) は u1(t) の時間微分に相当し、系の速度や変化率を表します。

4. タイトルと凡例:

  • グラフには「Solution of the Kadomtsev-Petviashvili Equation」というタイトルが表示されます。
  • 凡例には u1(t) と u2(t) のラベルが含まれ、どちらがどの曲線を表しているかが示されます。

5. グリッド:

  • グラフには背景にグリッドが表示され、各目盛りが値の参照を補助します。

このグラフを通じて、時間とともにカドモフ方程式の解がどのように振る舞うかを視覚的に理解することができます。

u1(t) と u2(t) の値の変化を見ながら、方程式が記述する現象や振る舞いを把握することができます。