ヘストネス方程式

ヘストネス方程式

ヘストネス方程式は、David Hestenes が1986年に提案した代数的な方程式です。

この方程式は、3次元空間における曲面の形状を記述するものです。

ヘストネス方程式は次のように表されます:

$$
(x^2 + y^2 + z^2 - 1)^3 - x^2y^3 - y^2z^3 - z^2x^3 = 0
$$

この方程式は、非線形の代数方程式で、左辺が$0$になる点の集合が曲面を表しています。

この曲面には以下のような特徴があります:

  1. 中心が原点$(0, 0, 0)$にあり、単位球面$(x^2 + y^2 + z^2 = 1)$に内接する曲面です。

  2. 曲面は滑らかではなく、いくつかの尖った部分があります。

  3. 曲面は$8$回対称性を持っています。
    つまり、座標軸周りに$45$度回転させても同じ形状になります。

  4. 曲面は自己交差しており、内部に空洞部分があります。

ヘストネス方程式は、幾何学的に興味深い性質を持つ代数方程式として知られており、コンピューター graphicsや数学の視覚化などで利用されています。

この方程式から得られる曲面は、複雑で美しい形状を持つため、芸術的な表現の題材にもなっています。

ソースコード

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np
import matplotlib.pyplot as plt

def hestenes_equation(x, y, z):
    return (x**2 + y**2 + z**2 - 1)**3 - x**2 * y**3 - y**2 * z**3 - z**2 * x**3

# Meshgridを作成
x = np.linspace(-1.5, 1.5, 50)
y = np.linspace(-1.5, 1.5, 50)
X, Y = np.meshgrid(x, y)

# 方程式を計算
Z = hestenes_equation(X, Y, 0)  # z=0の平面で計算

# 3D プロット
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Hestenes Equation')

plt.show()

上記のコードでは、まずHestenes方程式を定義する関数 hestenes_equation(x, y, z) を作成しています。

この関数は、与えられた x, y, z の値に対するHestenes方程式の値を返します。

次に、numpy を使って x と y の値の範囲を設定し、それらの値の組み合わせからメッシュグリッドを作成しています。

そして、z=0 の平面上でHestenes方程式を計算し、その結果を Z に格納しています。

最後に、matplotlib の plot_surface 関数を使って、計算された Z の値を3次元プロットしています。

実行すると、Hestenes方程式の立体的な曲面がプロットされます。

[実行結果]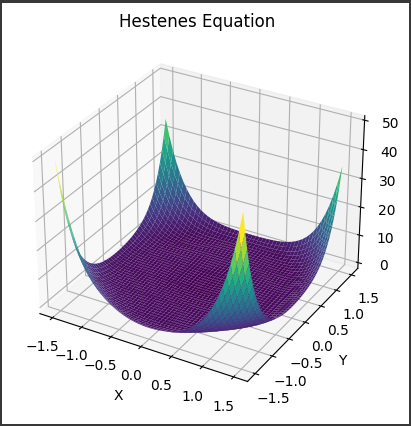

ソースコード解説

ソースコードを説明します。

1. ライブラリのインポート

1
2
import numpy as np
import matplotlib.pyplot as plt

最初に、NumPyとMatplotlibライブラリをインポートしています。
NumPyは数値計算を、Matplotlibはデータの可視化を行うためのPythonライブラリです。

2. Hestenes方程式の定義

1
2
def hestenes_equation(x, y, z):
    return (x**2 + y**2 + z**2 - 1)**3 - x**2 * y**3 - y**2 * z**3 - z**2 * x**3

Hestenes方程式を計算する関数hestenes_equationを定義しています。

この関数は、x、y、zの値を引数として受け取り、それらの値に対するHestenes方程式の値を返します。

3. メッシュグリッドの作成

1
2
3
x = np.linspace(-1.5, 1.5, 50)
y = np.linspace(-1.5, 1.5, 50)
X, Y = np.meshgrid(x, y)

NumPyのlinspace関数を使って、xとyの値の範囲を設定しています。
ここでは、$-1.5$から$1.5$までの$50$個の等間隔の値を生成しています。
次に、meshgrid関数を使って、xとyの値の組み合わせからメッシュグリッドを作成しています。

4. Hestenes方程式の計算

1
Z = hestenes_equation(X, Y, 0)  # z=0の平面で計算

先程定義したhestenes_equation関数を使って、メッシュグリッド上の各点における方程式の値を計算しています。
ここでは、z=0の平面上での値を計算しています。
計算結果はZに格納されます。

5. 3次元プロットの設定

1
2
3
4
5
6
7
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Hestenes Equation')

Matplotlibを使って、3次元プロットを設定しています。

まず、新しい図figを作成し、その中に3次元の座標軸axを追加しています。

次に、plot_surface関数を使って、計算されたZの値を3次元プロットしています。
rstrideとcstrideは、プロットする点の間隔を指定するパラメータです。
cmap='viridis'は、曲面の色を指定するためのカラーマップです。

最後に、軸のラベルとタイトルを設定しています。

6. プロットの表示

1
plt.show()

最後に、plt.show()を呼び出すことで、作成したプロットを表示します。

結果解説

[実行結果]

グラフに表示されている内容について説明します。

このグラフは3次元プロットで、Hestenes方程式から得られる曲面を可視化しています。

曲面の形状は以下のような特徴を持っています:

  1. 中心が原点$(0, 0, 0)$にあり、単位球面に内接しています。
    曲面の外形は球形に近い形をしています。

  2. 曲面は滑らかではなく、いくつかの鋭い尖った部分があります。
    特に、座標軸の正負方向に$4$つの主要な尖った部分があります。

  3. 曲面は$8$回対称性を持っており、座標軸周りに$45$度回転させても同じ形状になります。

  4. 曲面は自己交差しており、内部に空洞部分があります。
    曲面の内側には複雑な入り組んだ構造があり、一見すると次元が高い幾何学的な形状のようにも見えます。

  5. 曲面の色は、viridisカラーマップを使って高さに応じて色分けされています。
    原点付近は青紫色、高い部分は黄色がかった緑色になっています。

  6. グラフの背景は白で、曲面の形状が浮き立つようになっています。

  7. $X$軸、$Y$軸、$Z$軸のラベルと、タイトル「Hestenes Equation」が付けられています。

このようにHestenes方程式から得られる曲面は、非常に複雑で美しい形状を持っており、その幾何学的な特徴が3次元プロットによってよく可視化されています。