減衰調和振動(ダンプドハーモニックモーション)
減衰調和振動(ダンプドハーモニックモーション)は、振動系が外部抵抗(減衰力)によってエネルギーを失いながら振動する現象です。
減衰力は速度に比例し、振動の振幅が時間とともに減少します。
以下に、減衰調和振動について詳しく説明します。
【減衰調和振動の基本概念】
微分方程式
減衰調和振動は、以下の二階線形微分方程式で記述されます:
$$
m \frac{d^2x}{dt^2} + c \frac{dx}{dt} + kx = 0
$$
- $( m )$: 振動する物体の質量
- $( c )$: 減衰係数(速度に比例する抵抗力の係数)
- $( k )$: バネ定数(フックの法則に従うバネの硬さ)
- $( x(t) )$: 時間$ ( t ) $における変位
減衰の種類
減衰の強さによって、振動の挙動は次の3種類に分類されます:
- 過減衰 (Overdamping):
減衰が非常に大きいため、物体は振動せずに平衡位置に戻ります。 - 臨界減衰 (Critical Damping):
減衰が特定の臨界値に等しく、物体は最も速く平衡位置に戻りますが、振動しません。 - 減衰振動 (Underdamping):
減衰が比較的小さいため、物体は減衰しながら振動を続けます。
【減衰調和振動の解】
減衰調和振動の一般解は以下の形になります:
$$
x(t) = e^{-\frac{c}{2m} t} \left( A \cos(\omega_d t) + B \sin(\omega_d t) \right)
$$
- $( \omega_d = \sqrt{\frac{k}{m} - \left( \frac{c}{2m} \right)^2} ) $は減衰振動数(ダンピング振動数)
【減衰調和振動の特徴】
- 指数関数的減衰:
振幅は指数関数的に減少します。
減衰係数$ ( c ) $が大きいほど、振幅の減少が早くなります。 - 振動数の低下:
減衰があると、自然振動数$ ( \omega_0 = \sqrt{\frac{k}{m}} ) $よりも低い減衰振動数$ ( \omega_d ) $で振動します。
【減衰調和振動の物理的直感】
物理的な例として、減衰調和振動は次のようなシステムで観察されます:
- 自動車のサスペンション:
道路の凹凸による振動を抑えるための減衰装置が含まれます。 - 建物の制振装置:
地震時に建物の揺れを減衰させるためのダンパーが使用されます。 - メカニカルウォッチの振り子:
空気抵抗によって振り子の振動が徐々に減衰します。
【まとめ】
減衰調和振動は、多くの物理システムで観察される基本的な現象です。
減衰の影響で振幅が時間とともに減少し、エネルギーが徐々に失われるため、システムは最終的に静止状態に近づきます。
この現象を理解することで、振動を制御し、システムの安定性を向上させることが可能になります。
ソースコード
ダンプドハーモニックモーション(減衰調和振動)をPythonで2Dグラフ化する方法を示します。
以下のコードでは、Matplotlibライブラリを使用して時間経過に伴う振動の減衰をプロットします。
まず、減衰調和振動の微分方程式を以下のように定義します:
$$
m \frac{d^2x}{dt^2} + c \frac{dx}{dt} + kx = 0
$$
ここで、$m$は質量、$c$は減衰係数、$k$はバネ定数です。
この微分方程式の解は一般的に次のようになります:
$$
x(t) = e^{-\frac{c}{2m} t} \left( A \cos(\omega_d t) + B \sin(\omega_d t) \right)
$$
ここで、$ (\omega_d) $は減衰振動数で、
$$$
\omega_d = \sqrt{\frac{k}{m} - \left(\frac{c}{2m}\right)^2}
$$
です。
これを踏まえて、Pythonコードでグラフを描画します。
1 | import numpy as np |
このコードでは、次のステップを実行しています:
- パラメータ(質量 $m$、減衰係数 $c$、バネ定数 $k$、初期振幅 $A$、および初期速度に基づく項 $B$)の設定。
- 減衰振動数 $(\omega_d)$の計算。
- 時間範囲を設定(ここでは$0$から$20$秒までを$1000$ステップに分割)。
- 減衰調和振動の式に基づいて変位$x(t)$を計算。
Matplotlibを使用して2Dプロットを作成。- プロットにラベル、タイトル、グリッド、凡例を追加。
- プロットを表示。
このコードを実行することで、時間の経過に伴う減衰調和振動の挙動を2Dグラフで視覚化できます。
[実行結果]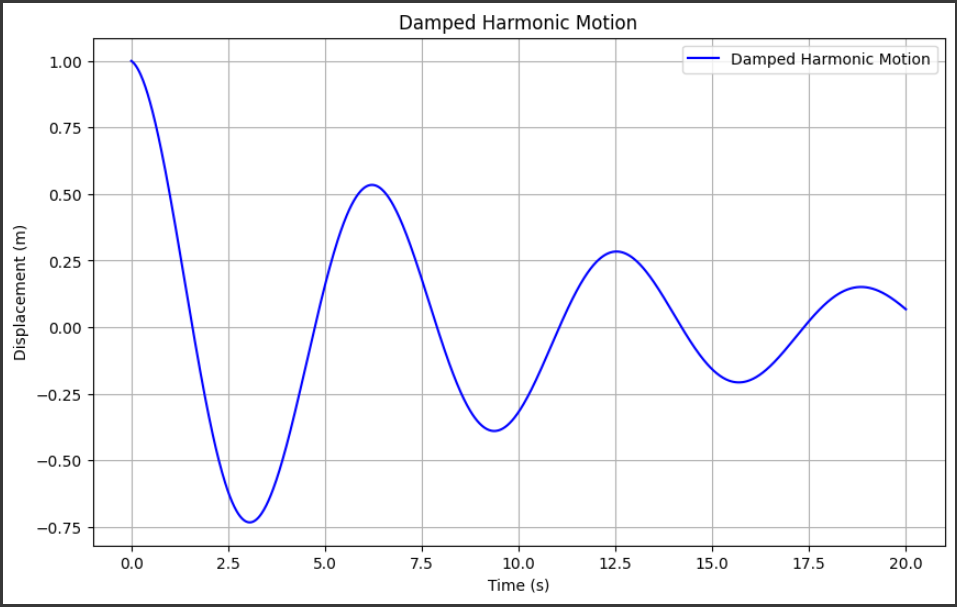
ソースコード解説
減衰調和振動のグラフを描画するために使用したPythonコードを詳細に説明します。
このグラフには、時間の経過に伴う物体の変位が表示されます。
各要素がどのように機能するかを説明します。
パラメータ設定
1 | m = 1.0 # 質量 |
m(質量): 振動する物体の質量です。c(減衰係数): 減衰の度合いを決定するパラメータです。値が大きいほど減衰が強くなります。k(バネ定数): バネの硬さを表します。A(初期振幅): 初期時点での振動の最大変位です。B(初期速度に基づく項): 初期速度がある場合に使いますが、ここでは$0$としています。
減衰振動数の計算
1 | omega_d = np.sqrt(k/m - (c/(2*m))**2) |
omega_d(減衰振動数): 減衰がある場合の振動数です。
減衰がない場合の自然振動数 $ (\omega_0 = \sqrt{k/m}) $から減衰項を引いて計算します。
時間の設定
1 | t = np.linspace(0, 20, 1000) |
t: 時間の配列です。
$0$秒から$20$秒までを$1000$ステップに分割しています。
これにより、時間の経過に伴う詳細な変位を計算できます。
減衰調和振動の式
1 | x = np.exp(-c/(2*m)*t) * (A * np.cos(omega_d * t) + B * np.sin(omega_d * t)) |
x: 時間tに対する変位です。
指数関数の項$ (\exp(-c/(2m) t)) $は減衰を表し、三角関数の項$ (\cos(\omega_d t)) $および$ (\sin(\omega_d t)) $は振動を表します。
2Dプロット
1 | plt.figure(figsize=(10, 6)) |
plt.figure(figsize=(10, 6)): グラフのサイズを設定しています。plt.plot(t, x, label='Damped Harmonic Motion', color='b'): 時間tに対する変位xを青色 (b) でプロットし、ラベルを「Damped Harmonic Motion」としています。
ラベルとタイトルの追加
1 | plt.xlabel('Time (s)') |
plt.xlabel('Time (s)'): x軸のラベルを「Time (s)」と設定しています。plt.ylabel('Displacement (m)'): y軸のラベルを「Displacement (m)」と設定しています。plt.title('Damped Harmonic Motion'): グラフのタイトルを「Damped Harmonic Motion」と設定しています。
グリッドと凡例の追加
1 | plt.grid(True) |
plt.grid(True): グラフにグリッド線を表示します。plt.legend(): グラフの凡例を表示します。
プロット表示
1 | plt.show() |
plt.show(): グラフを表示します。
グラフ解説
[実行結果]
このグラフは、時間の経過に伴う減衰調和振動の変位を示しています。
具体的には、以下の特徴があります:
1. 減衰の影響:
振幅が時間とともに指数関数的に減少します。
これは、減衰の影響によるものです。
2. 振動:
減衰していない場合の振動数よりも低い振動数で、減衰しながら振動します。
3. ゼロクロス:
振動がゼロを越える点がいくつかあり、これは物体が平衡位置を通過するたびに発生します。
このグラフを通じて、減衰調和振動の動的な挙動を視覚的に理解することができます。