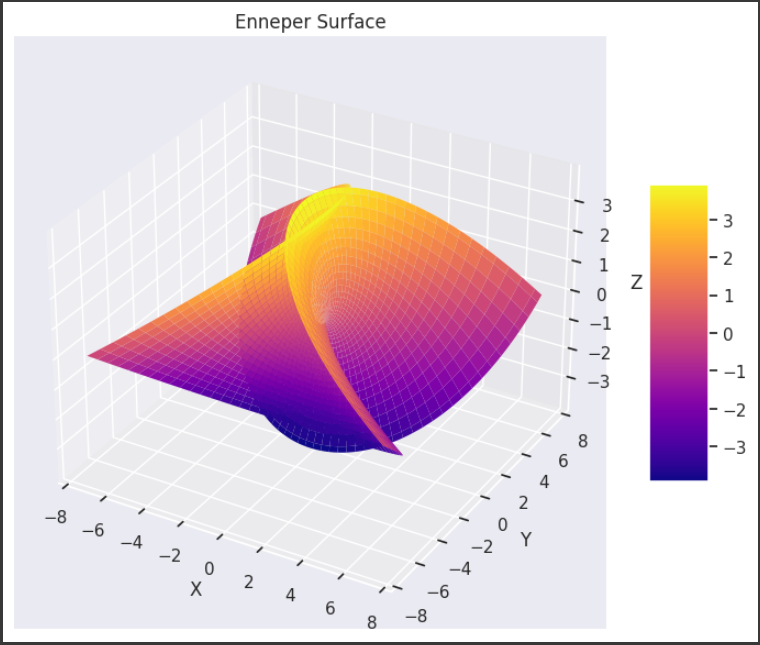
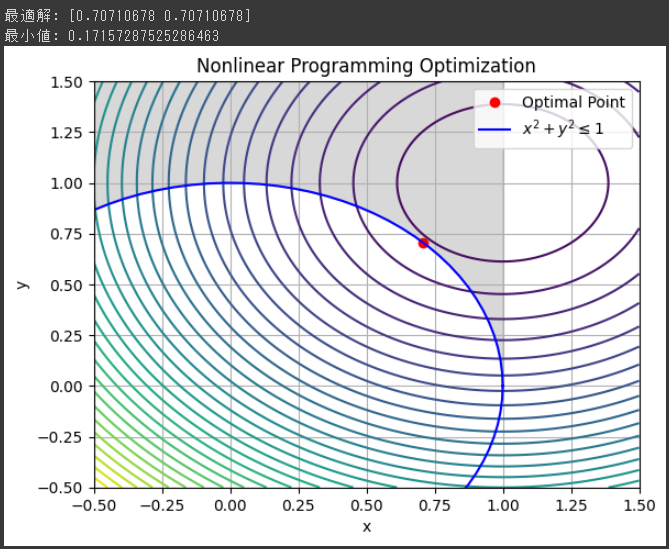
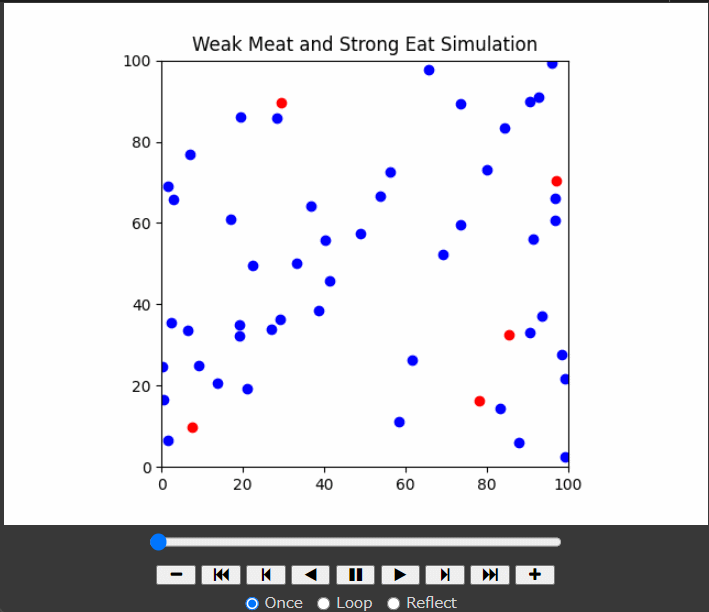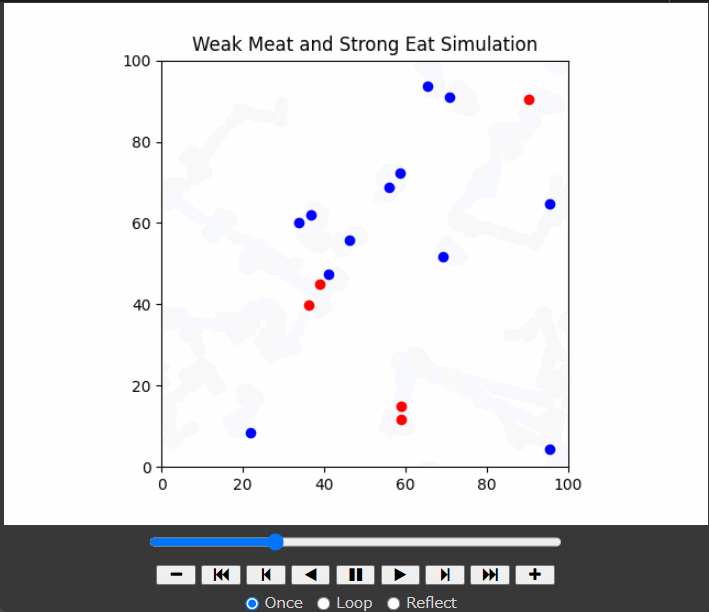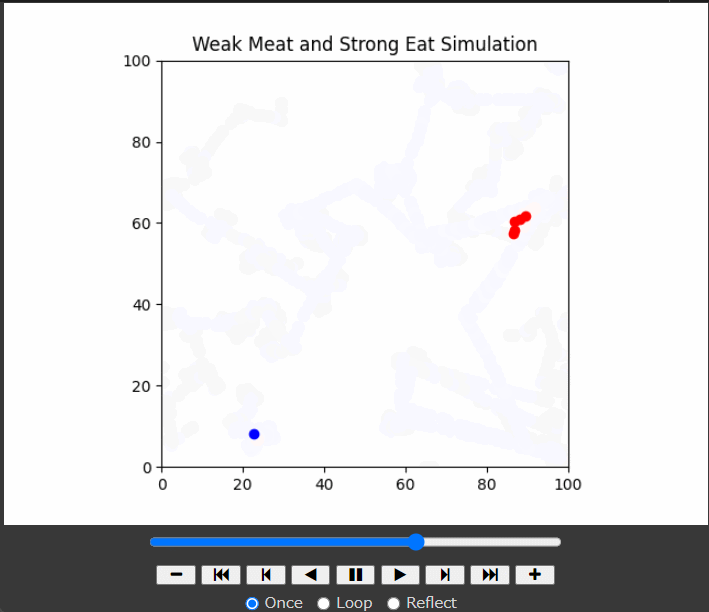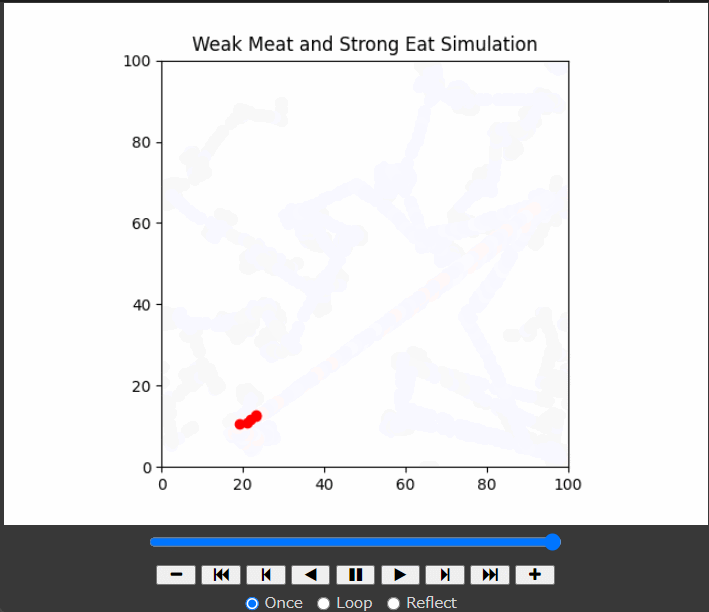
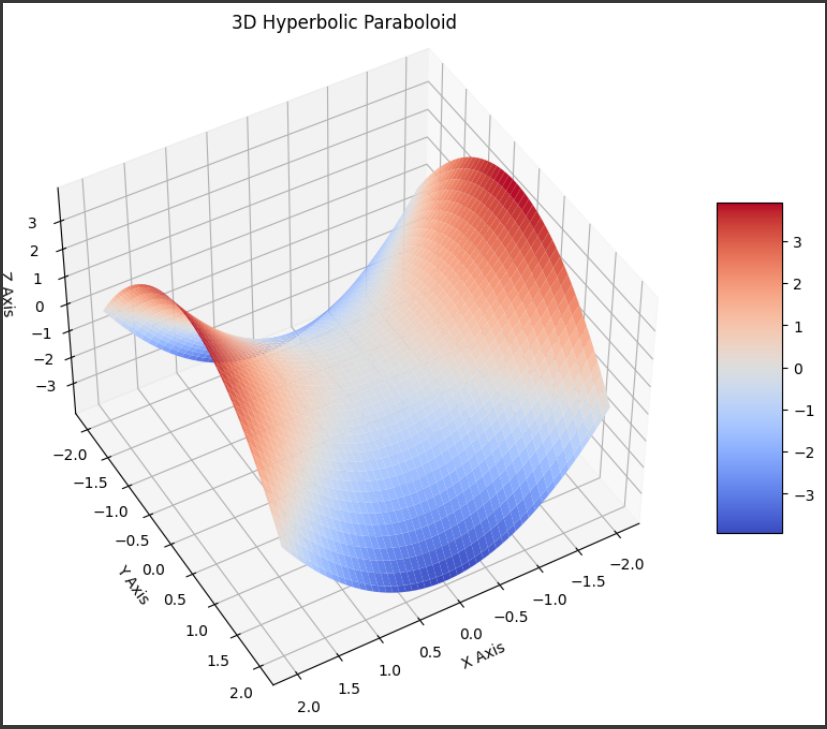
バーンズリーのシダ（Barnsley's fern）

バーンズリーのシダ（Barnsley’s fern）は、確率的な方法で生成されるフラクタル構造の一種であり、数学的な美しさと興味深さで知られています。

このシダは、数学者であるMichael Barnsleyによって導入されました。

バーンズリーのシダは、次のような確率的な方法で生成されます。

まず、初期条件として $(0, 0) $の点を選びます。

その後、一連の確率的な変換を適用して新しい点を生成します。

これらの変換は、特定の確率で選択され、シダの形を生成します。

バーンズリーのシダの生成には、以下のような変換が使用されます：

1. $1%$の確率で、点$ (x, y) $は$ (0, 0.16y) $に変換されます。
   これにより、葉の部分が生成されます。

2. $85%$の確率で、点$ (x, y) $は$ (0.85x + 0.04y, -0.04x + 0.85y + 1.6) $に変換されます。
   これにより、茎と枝が生成されます。

3. $7%$の確率で、点$ (x, y) $は$ (0.20x - 0.26y, 0.23x + 0.22y + 1.6) $に変換されます。
   これにより、さらに複雑な枝が生成されます。

4. $7%$の確率で、点$ (x, y) $は$ (-0.15x + 0.28y, 0.26x + 0.24y + 0.44) $に変換されます。
   これにより、より細かい枝が生成されます。

これらの変換を多数回繰り返すことで、バーンズリーのシダの構造が形成されます。

このフラクタル構造は、自然界に見られるシダの葉や枝の形状に類似しており、その美しさと複雑さから数学的な芸術の一形態として広く愛されています。

プログラム例

以下は、NetworkXを使用してバーンズリーのシダを生成し、グラフで表現するサンプルコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

import random
import networkx as nx
import matplotlib.pyplot as plt

# バーンズリーのシダ生成関数
def barnsley_fern(n):
    # 初期条件
    x, y = 0, 0
    points = [(x, y)]
    
    # バーンズリーのシダ生成
    for _ in range(n):
        r = random.random()
        if r <= 0.01:
            x, y = 0, 0.16 * y
        elif r <= 0.86:
            x, y = 0.85 * x + 0.04 * y, -0.04 * x + 0.85 * y + 1.6
        elif r <= 0.93:
            x, y = 0.20 * x - 0.26 * y, 0.23 * x + 0.22 * y + 1.6
        else:
            x, y = -0.15 * x + 0.28 * y, 0.26 * x + 0.24 * y + 0.44
        points.append((x, y))
    
    return points

# バーンズリーのシダを生成
fern_points = barnsley_fern(10000)

# グラフの作成
G = nx.Graph()

# ノードの追加
for i, (x, y) in enumerate(fern_points):
    G.add_node(i, pos=(x, y))

# エッジの追加
for i in range(len(fern_points) - 1):
    G.add_edge(i, i+1)

# グラフの描画
pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, node_size=0, edge_color='green', alpha=0.5, linewidths=0.5)
plt.title("Barnsley Fern using NetworkX")
plt.show()

このコードでは、バーンズリーのシダを生成するための関数 barnsley_fern を定義し、その結果をNetworkXのグラフに変換して描画しています。

生成されたグラフは、バーンズリーのシダの形を模倣した美しい構造を持っています。

[実行結果]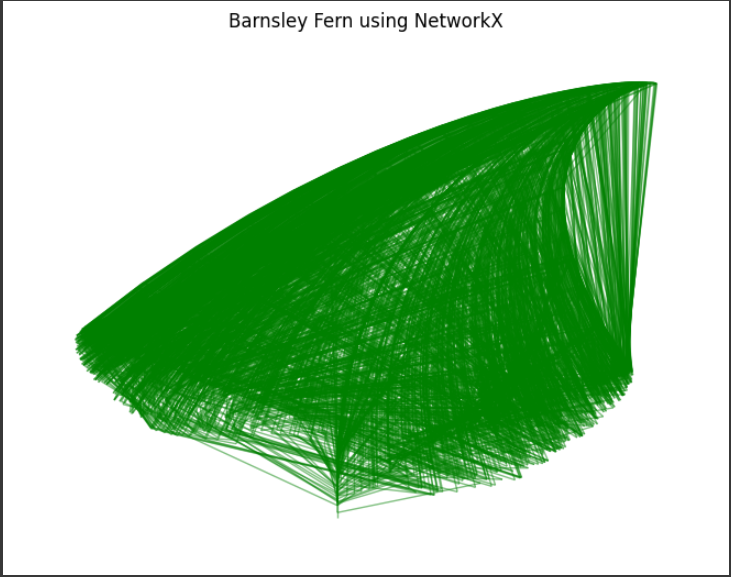

ソースコード解説

このソースコードは、Pythonを使用してバーンズリーのシダ（Barnsley’s fern）を生成し、NetworkXを使用してそのグラフを描画するものです。

以下では、コードの構造と各部分の役割について詳しく説明します。

1. バーンズリーのシダ生成関数の定義

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

def barnsley_fern(n):
    x, y = 0, 0  # 初期条件
    points = [(x, y)]  # 座標を格納するリスト

    # バーンズリーのシダ生成
    for _ in range(n):
        r = random.random()  # 0から1の乱数を生成
        if r <= 0.01:
            x, y = 0, 0.16 * y
        elif r <= 0.86:
            x, y = 0.85 * x + 0.04 * y, -0.04 * x + 0.85 * y + 1.6
        elif r <= 0.93:
            x, y = 0.20 * x - 0.26 * y, 0.23 * x + 0.22 * y + 1.6
        else:
            x, y = -0.15 * x + 0.28 * y, 0.26 * x + 0.24 * y + 0.44
        points.append((x, y))  # 新しい座標をリストに追加

    return points

この部分では、バーンズリーのシダを生成する関数 barnsley_fern が定義されています。

この関数は、生成する点の数 n を引数として受け取ります。

バーンズリーのシダは、一連の確率的な変換を繰り返すことで生成されます。

各ステップで、ランダムに選択された変換に基づいて新しい座標が計算され、リスト points に追加されます。

2. バーンズリーのシダを生成

1

fern_points = barnsley_fern(10000)

この行では、barnsley_fern 関数を呼び出して、$10000$個の点からなるバーンズリーのシダを生成し、fern_points に格納しています。

3. グラフの作成

1

G = nx.Graph()

この行では、NetworkXのグラフオブジェクト G を作成しています。

4. ノードの追加

1
2

for i, (x, y) in enumerate(fern_points):
    G.add_node(i, pos=(x, y))

この部分では、バーンズリーのシダで生成された点をグラフのノードとして追加しています。

各ノードには、座標を属性として持つことができます。

ここでは、各ノードに座標情報を pos という名前の属性として追加しています。

5. エッジの追加

1
2

for i in range(len(fern_points) - 1):
    G.add_edge(i, i+1)

この部分では、連続する点の間にエッジを追加しています。

これにより、シダの枝の構造が表現されます。

6. グラフの描画

1
2
3
4

pos = nx.get_node_attributes(G, 'pos')
nx.draw(G, pos, node_size=0, edge_color='green', alpha=0.5, linewidths=0.5)
plt.title("Barnsley Fern using NetworkX")
plt.show()

最後に、NetworkXの draw 関数を使用してグラフを描画しています。

ノードの座標は pos から取得し、それに基づいてノードとエッジが描画されます。

結果として得られるグラフは、バーンズリーのシダの形状を美しく表現しています。

輸送問題 (Transportation Problem)

最適化問題の例として、輸送問題 (Transportation Problem) を考えます。

この問題は、複数の供給地から複数の需要地に商品を輸送する際の輸送コストを最小化する問題です。

以下は簡単な輸送問題の例です。

問題設定:

• 供給地A、B、Cがあり、それぞれの供給量は次の通りです:
  • A: 20
  • B: 30
  • C: 25
• 需要地1、2、3があり、それぞれの需要量は次の通りです:
  • 1: 30
  • 2: 35
  • 3: 10
• 各供給地から各需要地への輸送コストは次のように設定されています:

この輸送問題を PuLP で解いてみましょう。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import pulp

# 供給量
supply = {'A': 20, 'B': 30, 'C': 25}

# 需要量
demand = {1: 30, 2: 35, 3: 10}

# 輸送コスト
cost = {'A': {1: 8, 2: 6, 3: 10},
        'B': {1: 9, 2: 12, 3: 13},
        'C': {1: 14, 2: 9, 3: 16}}

# 問題の定義
prob = pulp.LpProblem("Transportation_Problem", pulp.LpMinimize)

# 変数の定義
routes = [(i,j) for i in supply for j in demand]
vars = pulp.LpVariable.dicts("Route", (supply, demand), lowBound=0, cat='Continuous')

# 目的関数
prob += pulp.lpSum([vars[i][j] * cost[i][j] for (i, j) in routes])

# 制約条件
# 各供給地から出る供給量がその供給地の供給量に等しい
for i in supply:
    prob += pulp.lpSum([vars[i][j] for j in demand]) == supply[i]

# 各需要地に入る供給量がその需要地の需要量に等しい
for j in demand:
    prob += pulp.lpSum([vars[i][j] for i in supply]) == demand[j]

# 最適化の実行
prob.solve()

# 結果の表示
print("Status:", pulp.LpStatus[prob.status])
print("Total Cost:", pulp.value(prob.objective))
for v in prob.variables():
    print(v.name, "=", v.varValue)

このコードでは、供給地と需要地の間の輸送量を決定し、全体の輸送コストを最小化するように最適化しています。

最適化の結果に基づいて、どの供給地からどの需要地にいくらの商品を輸送すればコストが最小になるかを表示します。

[実行結果]

Status: Optimal
Total Cost: 655.0
Route_A_1 = 0.0
Route_A_2 = 10.0
Route_A_3 = 10.0
Route_B_1 = 30.0
Route_B_2 = 0.0
Route_B_3 = 0.0
Route_C_1 = 0.0
Route_C_2 = 25.0
Route_C_3 = 0.0

ソースコード解説

ソースコードを詳しく解説します。

1. 概要

このプログラムは、Pulpライブラリを使用して輸送問題を最適化する例です。

輸送問題は、供給地から需要地へ物資を輸送する際のコストを最小化するために、各ルートに割り当てる物資の量を決定する問題です。

2. 必要なライブラリのインポート

1

import pulp

• Pulpは、線形計画問題（LP）や整数計画問題（ILP）を解くためのPythonライブラリです。

3. データの定義

1
2
3
4
5
6
7
8
9
10

# 供給量
supply = {'A': 20, 'B': 30, 'C': 25}

# 需要量
demand = {1: 30, 2: 35, 3: 10}

# 輸送コスト
cost = {'A': {1: 8, 2: 6, 3: 10},
        'B': {1: 9, 2: 12, 3: 13},
        'C': {1: 14, 2: 9, 3: 16}}

• 供給量: 各供給地の供給量を表します。
• 需要量: 各需要地の需要量を表します。
• 輸送コスト: 各供給地から需要地への輸送コストを表します。

4. 問題の定義

1

prob = pulp.LpProblem("Transportation_Problem", pulp.LpMinimize)

• 輸送問題を最小化問題として定義します。ここでは、輸送コストを最小化することが目的です。

5. 変数の定義

1
2

routes = [(i,j) for i in supply for j in demand]
vars = pulp.LpVariable.dicts("Route", (supply, demand), lowBound=0, cat='Continuous')

• routes: 全ての供給地と需要地の組み合わせをリストにします。
• vars: 各ルートにおける輸送量を表す変数を定義します。ここでは、連続変数として定義しています。

6. 目的関数の定義

1

prob += pulp.lpSum([vars[i][j] * cost[i][j] for (i, j) in routes])

• 目的関数は、全てのルートにおける輸送コストの総和を最小化することです。

7. 制約条件の定義

1
2
3
4
5
6
7

# 各供給地から出る供給量がその供給地の供給量に等しい
for i in supply:
    prob += pulp.lpSum([vars[i][j] for j in demand]) == supply[i]

# 各需要地に入る供給量がその需要地の需要量に等しい
for j in demand:
    prob += pulp.lpSum([vars[i][j] for i in supply]) == demand[j]

• 供給制約: 各供給地から出る供給量が、その供給地の供給量に等しくなるようにします。
• 需要制約: 各需要地に入る供給量が、その需要地の需要量に等しくなるようにします。

8. 最適化の実行

1

prob.solve()

• Pulpのsolveメソッドを使用して、定義した問題を解きます。

9. 結果の表示

1
2
3
4

print("Status:", pulp.LpStatus[prob.status])
print("Total Cost:", pulp.value(prob.objective))
for v in prob.variables():
    print(v.name, "=", v.varValue)

• 最適化のステータス（成功・失敗）を表示します。
• 最小化された総輸送コストを表示します。
• 各ルートにおける最適な輸送量を表示します。

結果解説

この実行結果を詳しく解説します。

[実行結果]

Status: Optimal
Total Cost: 655.0
Route_A_1 = 0.0
Route_A_2 = 10.0
Route_A_3 = 10.0
Route_B_1 = 30.0
Route_B_2 = 0.0
Route_B_3 = 0.0
Route_C_1 = 0.0
Route_C_2 = 25.0
Route_C_3 = 0.0

結果:

• 最適化ステータス: Optimal
  • この結果は、PuLPが問題に対して最適な解を見つけたことを示しています。
• 総輸送コスト: 655.0
  • この値は、最適な輸送計画に基づいて計算された最小の総コストです。

各供給地から各需要地への輸送量:

• Route_A_1 = 0.0
  • 供給地Aから需要地1への輸送量は 0 です。
• Route_A_2 = 10.0
  • 供給地Aから需要地2への輸送量は 10 です。
• Route_A_3 = 10.0
  • 供給地Aから需要地3への輸送量は 10 です。
• Route_B_1 = 30.0
  • 供給地Bから需要地1への輸送量は 30 です。
• Route_B_2 = 0.0
  • 供給地Bから需要地2への輸送量は 0 です。
• Route_B_3 = 0.0
  • 供給地Bから需要地3への輸送量は 0 です。
• Route_C_1 = 0.0
  • 供給地Cから需要地1への輸送量は 0 です。
• Route_C_2 = 25.0
  • 供給地Cから需要地2への輸送量は 25 です。
• Route_C_3 = 0.0
  • 供給地Cから需要地3への輸送量は 0 です。

解釈

この結果から、以下の輸送プランがコストを最小化するために用いられます。

• 供給地A:
  • 需要地2に 10 単位を輸送します。 (コスト: $(6 \times 10 = 60)$)
  • 需要地3に 10 単位を輸送します。 (コスト: $(10 \times 10 = 100)$)
• 供給地B:
  • 需要地1に 30 単位を輸送します。 (コスト: $(9 \times 30 = 270)$)
• 供給地C:
  • 需要地2に 25 単位を輸送します。 (コスト: $(9 \times 25 = 225)$)

総コストの計算

上記の輸送プランに基づいた輸送コストは次のように計算できます。

• 供給地Aのコスト: $(60 + 100 = 160)$
• 供給地Bのコスト: $(270)$
• 供給地Cのコスト: $(225)$

したがって、合計の輸送コストは下記のようになります。
$$
160 + 270 + 225 = 655
$$

エンネーパーの面（Enneper Surface）

エンネーパーの面（Enneper Surface）は、微分幾何学における特異な極小曲面の一例であり、以下の特徴を持ちます：

特徴

1. 極小曲面：

   • エンネーパーの面は、曲面上の任意の点で曲率が最小となる極小曲面です。
     極小曲面は、物理的には石鹸膜のように、表面積を最小化する形状を取る面です。

2. 自己交差：

   • エンネーパーの面は、自己交差する点を持ちます。
     つまり、曲面の一部が別の部分と交差する点が存在します。

3. パラメトリック方程式：

   • エンネーパーの面は、以下のパラメトリック方程式で定義されます：
     $$
     x(u, v) = u - \frac{u^3}{3} + u v^2
     $$
     $$
     y(u, v) = v - \frac{v^3}{3} + v u^2
     $$
     $$
     z(u, v) = u^2 - v^2
     $$
     ここで、$(u) $と$ (v) $はパラメータです。

4. 対称性：

   • エンネーパーの面は、対称性を持つ曲面であり、中心対称的な形状をしています。
     曲面は中央部分から外側に向かって曲がりくねる形状を持ち、対称的に広がります。

5. 幾何学的美しさ：

   • エンネーパーの面は、その複雑で滑らかな形状から、数学的にも美しい曲面として知られています。

例

エンネーパーの面は、数学的研究や教育においてよく使用される曲面で、極小曲面の典型例として知られています。

コンピュータグラフィックスや芸術的なデザインにおいても、その独特の形状が利用されることがあります。

視覚的な説明

エンネーパーの面を視覚化すると、以下のような特徴が見られます：

• 曲面は中央部で交差し、内側にくびれた形状を形成します。
• 高さの違いによって色が変わるカラーマップを適用することで、曲面の高低差が視覚的に強調されます。

エンネーパーの面は、その独特の形状と数学的特性から、微分幾何学における重要な研究対象の一つです。

プログラム例

以下にPythonコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns

# seabornのスタイルを使用
sns.set(style='darkgrid')

# パラメータの範囲を設定
u = np.linspace(-2, 2, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

# エンネーパーの面のパラメトリック方程式
x = u - (u**3) / 3 + u * v**2
y = v - (v**3) / 3 + v * u**2
z = u**2 - v**2

# プロットを作成
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')

# 3Dサーフェスプロット
surf = ax.plot_surface(x, y, z, cmap='plasma', edgecolor='none')

# カラーバーを追加
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)

# 軸ラベル
ax.set_xlabel('X軸')
ax.set_ylabel('Y軸')
ax.set_zlabel('Z軸')

# タイトルを追加
ax.set_title('Enneper Surface')

# グラフを表示
plt.show()

このコードを実行すると、エンネーパーの面の3Dプロットが描画されます。

学術的に興味深い形状を持つエンネーパーの面を使って、複雑な3Dグラフを表示します。

[実行結果]

ソースコード解説

ソースコードを詳しく説明します。

1. 必要なライブラリのインポート

1
2
3
4

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns

このセクションでは、以下のライブラリをインポートしています。

• numpy: 数値計算を効率的に行うためのライブラリ。
• matplotlib.pyplot: グラフ作成のためのライブラリ。
• mpl_toolkits.mplot3d: 3Dプロットをサポートするためのライブラリ。
• seaborn: 見栄えの良いグラフを作成するためのライブラリ。

2. Seabornスタイルの設定

1
2

# seabornのスタイルを使用
sns.set(style='darkgrid')

Seabornのスタイルをdarkgridに設定しています。
これにより、プロットの背景がダークグリッドスタイルになります。

3. パラメータの範囲を設定

1
2
3
4

# パラメータの範囲を設定
u = np.linspace(-2, 2, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

ここでは、uとvの範囲を-2から2まで$100$等分した配列を作成しています。
その後、np.meshgridを使用して2次元のグリッドデータを作成しています。

4. エンネーパーの面のパラメトリック方程式

1
2
3
4

# エンネーパーの面のパラメトリック方程式
x = u - (u**3) / 3 + u * v**2
y = v - (v**3) / 3 + v * u**2
z = u**2 - v**2

エンネーパーの面のパラメトリック方程式を使って、x, y, zの座標を計算しています。

5. プロットの作成

1
2
3

# プロットを作成
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')

figオブジェクトを作成し、サイズを設定しています。
次に、3Dプロット用のaxオブジェクトを追加しています。

6. 3Dサーフェスプロット

1
2

# 3Dサーフェスプロット
surf = ax.plot_surface(x, y, z, cmap='plasma', edgecolor='none')

ax.plot_surfaceを使用して、x, y, zのデータを基に3Dサーフェスプロットを作成しています。
色のマッピングにはplasmaカラーマップを使用し、エッジの色を無くしています。

7. カラーバーの追加

1
2

# カラーバーを追加
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)

サーフェスプロットに対応するカラーバーを追加しています。
shrinkでカラーバーのサイズを調整し、aspectでアスペクト比を設定しています。

8. 軸ラベルの設定

1
2
3
4

# 軸ラベル
ax.set_xlabel('X軸')
ax.set_ylabel('Y軸')
ax.set_zlabel('Z軸')

3Dプロットの各軸にラベルを設定しています。

9. タイトルの追加

1
2

# タイトルを追加
ax.set_title('Enneper Surface')

3Dプロットにタイトルを追加しています。

10. グラフの表示

1
2

# グラフを表示
plt.show()

最終的に、plt.show()を使用してグラフを表示しています。

以上が、コードの詳細な説明です。

各ステップがどのように3Dプロットを作成するために機能しているかを理解することで、同様の3Dプロットを作成する際に応用することができます。

結果解説

[実行結果]

このグラフは、エンネーパーの面（Enneper Surface）を3Dで表示したものです。

エンネーパーの面は、数学や幾何学で知られる特異な曲面で、以下のような特徴を持っています：

1. 形状：

エンネーパーの面は、曲線的で非線形な形状を持ち、複雑な対称性を示します。
表面は中央部から外側に向かって曲がりくねり、波打つような形状になっています。

2. カラーマップ：

plasmaというカラーマップが使用されており、表面の高さや深さに応じて色が変化します。
これにより、3D構造の高低差が視覚的にわかりやすくなっています。

3. 軸：

• X軸：横方向の軸。
• Y軸：縦方向の軸。
• Z軸：高さ方向の軸。

4. カラーバー：

グラフの右側にカラーバーが表示されており、色と高さの対応関係を示しています。
これにより、特定の色がどの高さを表しているかがわかります。

このグラフは、エンネーパーの面の複雑な幾何学的特徴を直感的に理解できるように可視化しています。

非線形計画法（Nonlinear Programming、NLP）

非線形計画法（Nonlinear Programming、NLP）は、目的関数と制約条件が非線形となる最適化問題を扱います。

今回は、非線形最適化の典型的な例題として、以下の問題を考えます。

例題

最小化する関数と条件は以下の通りです。

$$
\text{minimize } f(x, y) = (x-1)^2 + (y-1)^2
$$

制約条件:

$$
g_1(x, y) = x^2 + y^2 - 1 \leq 0
$$
$$
g_2(x, y) = x \geq 0
$$
$$
g_3(x, y) = y \geq 0
$$

この問題をPythonのscipy.optimizeを使って解き、その結果をグラフ化します。

必要なライブラリのインストール

Google Colab環境で以下のコマンドを実行して必要なライブラリをインストールします。

1

!pip install scipy matplotlib

コード

以下がこの問題を解き、その結果をグラフ化するPythonコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 最適化する関数の定義
def objective_function(x):
    return (x[0] - 1)**2 + (x[1] - 1)**2

# 制約条件の定義
def constraint1(x):
    return 1 - (x[0]**2 + x[1]**2)  # x^2 + y^2 <= 1 に対応

# 境界条件の定義
bounds = [(0, None), (0, None)]  # x >= 0, y >= 0

# 制約条件のリスト
constraints = [{'type': 'ineq', 'fun': constraint1}]

# 初期点
x0 = [0.5, 0.5]

# 最適化の実行
result = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=constraints)

# 結果の出力
print('最適解:', result.x)
print('最小値:', result.fun)

# 結果のグラフ化
x = np.linspace(-0.5, 1.5, 400)
y = np.linspace(-0.5, 1.5, 400)
X, Y = np.meshgrid(x, y)
Z = (X - 1)**2 + (Y - 1)**2

plt.contour(X, Y, Z, levels=30)
plt.plot(result.x[0], result.x[1], 'ro', label='Optimal Point')  # 最適解を赤い点でプロット

# 制約条件の境界線をプロット
theta = np.linspace(0, 2*np.pi, 100)
x_circle = np.cos(theta)
y_circle = np.sin(theta)
plt.plot(x_circle, y_circle, 'b-', label='$x^2 + y^2 \leq 1$')

plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1.5)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Nonlinear Programming Optimization')
plt.grid(True)
plt.legend()
plt.fill_between(x_circle, y_circle, 1.5, where=(y_circle >= 0), alpha=0.3, color='gray')  # 可行領域
plt.show()

解説

1. 最適化する関数の定義:
   目的関数 $ ( f(x, y) = (x-1)^2 + (y-1)^2 ) $を定義します。

2. 制約条件の定義:
   非線形制約 $ ( g_1(x, y) = x^2 + y^2 - 1 \leq 0 ) $を定義します。

3. 境界条件の定義:
   $( x \geq 0 ) $および$ ( y \geq 0 ) $に対応する境界条件を定義します。

4. 制約条件のリスト constraints:
   制約条件をリスト形式で定義します。

5. 初期点の設定 x0:
   最適化アルゴリズムの初期点を設定します。

6. 最適化の実行 result:
   scipy.optimize.minimize を使用して最適化を実行します。
   methodにはSLSQP（Sequential Least Squares Programming）を使用します。

7. 結果の出力:
   得られた最適解と最小値を表示します。

8. グラフ化:

   • 目的関数の等高線を描画。
   • 制約条件 $ ( x^2 + y^2 \leq 1 ) $の境界線を描画。
   • 最適解を赤い点でプロット。
   • 制約条件を満たす領域を灰色で塗りつぶします。

以上で、非線形最適化問題の解と制約条件を含む結果をグラフで視覚的に確認できます。

実行結果

弱肉強食シミュレーション

弱肉強食の様子をアニメーションで視覚化するために、プレデター（捕食者）とプレイ（被食者）の関係をシミュレートするプログラムを作成します。

matplotlib.animationモジュールを使用して、シミュレーションの進行状況をリアルタイムで描画します。

以下は、プレデターとプレイのシミュレーションを行い、その様子をアニメーションとして可視化するPythonコードです。

（以下のコードは、Google Colab上で動作確認できます。）

必要なパッケージのインストール

まず、必要なパッケージをインストールします。

1

!pip install matplotlib numpy

Pythonコード

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTML

# パラメータ
num_prey = 50  # 被食者の数
num_predator = 5  # 捕食者の数
world_size = (100, 100)  # 世界のサイズ
prey_speed = 1  # 被食者の移動速度
predator_speed = 1.5  # 捕食者の移動速度

# 被食者クラス
class Prey:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def move(self):
        self.x = (self.x + np.random.uniform(-prey_speed, prey_speed)) % world_size[0]
        self.y = (self.y + np.random.uniform(-prey_speed, prey_speed)) % world_size[1]

# 捕食者クラス
class Predator:
    def __init__(self, x, y):
        self.x = x
        self.y = y

    def move(self, prey_list):
        if prey_list:
            # 最も近い被食者を探す
            prey = min(prey_list, key=lambda p: (p.x - self.x)**2 + (p.y - self.y)**2)
            dx = prey.x - self.x
            dy = prey.y - self.y
            dist = np.sqrt(dx**2 + dy**2)
            if dist > 0:
                self.x = (self.x + predator_speed * dx / dist) % world_size[0]
                self.y = (self.y + predator_speed * dy / dist) % world_size[1]

        # 捕食チェック
        for prey in prey_list.copy():
            if np.sqrt((prey.x - self.x)**2 + (prey.y - self.y)**2) < 1:
                prey_list.remove(prey)

# 初期化
preys = [Prey(np.random.uniform(0, world_size[0]), np.random.uniform(0, world_size[1])) for _ in range(num_prey)]
predators = [Predator(np.random.uniform(0, world_size[0]), np.random.uniform(0, world_size[1])) for _ in range(num_predator)]

fig, ax = plt.subplots()
scat_prey = ax.scatter([prey.x for prey in preys], [prey.y for prey in preys], c='blue')
scat_pred = ax.scatter([pred.x for pred in predators], [pred.y for pred in predators], c='red')
plt.xlim(0, world_size[0])
plt.ylim(0, world_size[1])
plt.gca().set_aspect('equal', adjustable='box')
plt.title('Weak Meat and Strong Eat Simulation')

def update(frame):
    for prey in preys:
        prey.move()
    for pred in predators:
        pred.move(preys)
        
    scat_prey.set_offsets(np.c_[[prey.x for prey in preys], [prey.y for prey in preys]])
    scat_pred.set_offsets(np.c_[[pred.x for pred in predators], [pred.y for pred in predators]])
    return scat_prey, scat_pred

ani = FuncAnimation(fig, update, frames=200, interval=100, blit=True)

# アニメーションをHTMLとして表示する
HTML(ani.to_jshtml())

コードの説明

1. インストールとインポート:
   必要なパッケージをインストールし、インポートします。

2. パラメータの設定:

   1 2 3 4 5

   num_prey = 50 # 被食者の数 num_predator = 5 # 捕食者の数 world_size = (100, 100) # 世界のサイズ prey_speed = 1 # 被食者の移動速度 predator_speed = 1.5 # 捕食者の移動速度

3. 被食者と捕食者のクラス定義:
   前述の通り、被食者と捕食者の移動ロジックを定義します。

4. 初期化:
   被食者と捕食者の位置をランダムに初期化します。

   1 2	preys = [Prey(np.random.uniform(0, world_size[0]), np.random.uniform(0, world_size[1])) for _ in range(num_prey)] predators = [Predator(np.random.uniform(0, world_size[0]), np.random.uniform(0, world_size[1])) for _ in range(num_predator)]

5. アニメーションの設定:
   アニメーション更新関数を設定し、FuncAnimationを使用してアニメーションを作成します。

   1	ani = FuncAnimation(fig, update, frames=200, interval=100, blit=True)

6. アニメーションの表示:
   HTML形式でアニメーションを表示します。

   1	HTML(ani.to_jshtml())

このコードをGoogle Colabで実行すると、弱肉強食の様子がアニメーションとして表示されます。

結果解説

[実行結果]

アニメーションの様子を具体的に理解するためには、シミュレーションがどのように進行し、どのような視覚効果があるのかを詳しく説明します。

アニメーションの概要

このシミュレーションとアニメーションは、シンプルなエコシステムをモデル化しています。
シミュレーション内で、青い点は被食者（プレイ）、赤い点は捕食者（プレデター）を表しています。
これらの点が指定されたルールに従って移動し、捕食の様子がリアルタイムで表示されます。

初期状態

• 被食者（青い点）：
  • 数量：$50$
  • ランダムな位置に配置され、移動速度は$1$です。
• 捕食者（赤い点）：
  • 数量：$5$
  • ランダムな位置に配置され、移動速度は$1.5$です。

アニメーションの進行

1. 被食者の移動：

   • 被食者は毎フレームごとにランダムな方向に少しずつ移動します。
   • 移動範囲は、世界サイズ（100x100）の中でラップアラウンド（画面端から反対側に移動）します。

2. 捕食者の移動：

   • 捕食者は最も近い被食者を追いかけます。
     具体的には、次のステップで被食者との距離が最も小さくなる方向に移動します。
   • 捕食者も同様に世界サイズ（100x100）の中でラップアラウンドします。

3. 捕食チェック：

   • 捕食者が被食者に非常に近づいた場合（距離が1未満）、その被食者は捕食されてリストから削除されます。

アニメーションのビジュアル効果

• 被食者は青い点として、捕食者は赤い点として表示されます。
• 被食者が捕食されると、その青い点は消え、アニメーション進行中に点の数が減少します。
• アニメーションは200フレーム間で進行し、各フレームごとに被食者と捕食者の位置が更新され、描画されます。

実行の様子

1. 開始時：

   • 画面にはランダムに配置された多くの青い点（被食者）と少数の赤い点（捕食者）が表示されます。

2. 中盤：

   • 青い点がランダムに動き回る一方で、赤い点が最も近い青い点を追いかける様子が確認できます。
   • 捕食が成功すると、青い点が消える様子が見えます。

3. 終了時：

   • 多くの青い点が捕食され、減少しています。
   • 赤い点が依然として動き回り、残った青い点を追いかけ続けます。

線形計画問題（Linear Programming Problem）

目的最適化の一つの例として、線形計画問題（Linear Programming Problem）を挙げることができます。

以下に、シンプルな線形計画問題をPythonで解く方法を示します。

ここではscipy.optimize.linprogを使います。

例題

問題の目的は、以下の制約条件を満たしつつ、次の目的関数を最小化することです。

目的関数:

$
f(x, y) = 3x + 4y
$

制約条件:

1. $( x + 2y \geqq 4 )$
2. $( 3x + y \geqq 3 )$
3. $( x \geqq 0 )$
4. $( y \geqq 0 )$

この問題をPythonで解く方法を以下に示します。

Pythonコード:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
from scipy.optimize import linprog

# 目的関数の係数
c = np.array([3, 4])

# 制約条件の係数行列
A = np.array([[-1, -2], [-3, -1]])

# 制約条件の右辺ベクトル
b = np.array([-4, -3])

# 変数の下限定義 (x ≥ 0, y ≥ 0)
x_bounds = (0, None)
y_bounds = (0, None)

# linprog関数を使って問題を解く
result = linprog(c, A_ub=A, b_ub=b, bounds=[x_bounds, y_bounds], method='highs')

# 結果を表示
if result.success:
    print("最適解:", result.x)
    print("目的関数値:", result.fun)
else:
    print("最適化は成功しませんでした。")

[実行結果]

解説

1. 目的関数の係数: c = [3, 4]

   • 目的関数 $ ( f(x, y) = 3x + 4y ) $の係数です。

2. 制約条件の係数行列: A = [[-1, -2], [-3, -1]]

   • 制約条件を標準形$（ (Ax \leqq b) ）$にするために、不等式の符号を反転させています。

3. 制約条件の右辺ベクトル: b = [-4, -3]

   • 同様に符号を反転させた右辺ベクトルです。

4. 変数の下限定義: x_bounds = (0, None), y_bounds = (0, None)

   • 変数$ (x, y) $が非負であることを示しています。

5. linprog関数の実行:

   • 目的関数、制約条件、変数の範囲を指定して、線形計画問題を解きます。
   • method='highs' は最先端のアルゴリズムを使って最適化を行うオプションです。

6. 結果の表示:

   • result.success が True の場合、最適解と目的関数値を表示します。

このようにして、この線形計画問題の最適化をPythonコードで解くことができます。

粒子群最適化（Particle Swarm Optimization, PSO）

粒子群最適化（Particle Swarm Optimization, PSO）は、進化的アルゴリズムの一種で、群知能を利用して最適解を見つける手法です。

具体的な問題として、ここでは以下の二次関数の最小化問題を解いてみます：

$$
f(x, y) = (x - 3)^2 + (y - 2)^2
$$

この関数の最小値を探すことが目的です。

この関数はパラボロイドであり、最小値は点$ ( (3, 2) ) $で$ 0 $となります。

以下にPythonを使ったPSOの具体的なコード例を示します。

このコードでは、PyGMOライブラリを使ってPSOを実装します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

import pygmo as pg
import numpy as np
import matplotlib.pyplot as plt

# 最適化したい関数の定義
def objective_function(x):
    return (x[0] - 3)**2 + (x[1] - 2)**2

# 問題の定義
class MyProblem:
    def fitness(self, x):
        return [objective_function(x)]
    def get_bounds(self):
        return ([-10, -10], [10, 10])

# 問題のインスタンスを作成
prob = pg.problem(MyProblem())

# アルゴリズムの選択 (PSO)
algo = pg.algorithm(pg.pso(gen=100))  # 100世代

# アルゴリズムのインスタンスを作成
algo.set_verbosity(1)

# 集団 (swarm) の定義
pop = pg.population(prob, size=20)

# 最適化の実行
pop = algo.evolve(pop)

# 最適化結果の取得
best_solution = pop.champion_x
best_fitness = pop.champion_f

print(f"Best solution: {best_solution}")
print(f"Best fitness: {best_fitness}")

# グラフの描画
# 評価関数の値をカラーマップでプロット
x = np.linspace(-10, 10, 400)
y = np.linspace(-10, 10, 400)
X, Y = np.meshgrid(x, y)
Z = objective_function([X, Y])

plt.contourf(X, Y, Z, levels=50, cmap='viridis')
plt.colorbar()
plt.plot(best_solution[0], best_solution[1], 'ro')  # 最適解を赤い点でプロット
plt.title("Particle Swarm Optimization Result")
plt.xlabel("x")
plt.ylabel("y")
plt.show()

ソースコード解説

1. 必要なライブラリのインポート

1
2
3

import pygmo as pg
import numpy as np
import matplotlib.pyplot as plt

PyGMO、NumPy、Matplotlibライブラリをインポートします。

2. 最適化したい関数の定義

1
2

def objective_function(x):
    return (x[0] - 3)**2 + (x[1] - 2)**2

ここで、最小化したい二次関数を定義します。

3. 最適化問題の定義

1
2
3
4
5

class MyProblem:
    def fitness(self, x):
        return [objective_function(x)]
    def get_bounds(self):
        return ([-10, -10], [10, 10])

PyGMOが理解できる形式で問題を定義します。
この例では、解の範囲を$ -10 $から$ 10 $とします。

4. 問題インスタンスの作成

1

prob = pg.problem(MyProblem())

最適化問題のインスタンスを作成します。

5. アルゴリズムの選択

1

algo = pg.algorithm(pg.pso(gen=100))  # 100世代

PSOアルゴリズムを選択し、世代数を設定します。

6. アルゴリズムインスタンスの作成

1

algo.set_verbosity(1)

アルゴリズムの詳細な実行状況を表示するように設定します。

7. 集団の定義

1

pop = pg.population(prob, size=20)

解の集団（swarm）を定義します。
ここでは $20$ 個体で初期化します。

8. 最適化の実行

1

pop = algo.evolve(pop)

最適化を実行します。

9. 最適化結果の取得

1
2
3
4
5

best_solution = pop.champion_x
best_fitness = pop.champion_f

print(f"Best solution: {best_solution}")
print(f"Best fitness: {best_fitness}")

最適な解とその評価値を取得し、表示します。

10. グラフの描画

1
2
3
4
5
6
7
8
9
10
11
12

x = np.linspace(-10, 10, 400)
y = np.linspace(-10, 10, 400)
X, Y = np.meshgrid(x, y)
Z = objective_function([X, Y])

plt.contourf(X, Y, Z, levels=50, cmap='viridis')
plt.colorbar()
plt.plot(best_solution[0], best_solution[1], 'ro')  # 最適解を赤い点でプロット
plt.title("Particle Swarm Optimization Result")
plt.xlabel("x")
plt.ylabel("y")
plt.show()

評価関数のカラーマップをプロットし、最適解を赤い点で示します。

結果解説

[実行結果]

最適化結果の解釈

• Best solution: [2.99999768, 2.00000504]

  • これはPSOアルゴリズムによって見つかった最適解です。
    関数$ ( f(x, y) = (x - 3)^2 + (y - 2)^2 ) $の最小値を見つけるために、PSOが探索した結果、最適解が$ ( x \approx 3 ) と ( y \approx 2 ) $に非常に近い値であることが示されています。

• Best fitness: [3.07979981e-11]

  • これは最適解における関数の値（評価値）です。
    最小化したい関数の最小値は$ 0 $ですが、見つけた最適解での関数値は$ ( 3.07979981 \times 10^{-11} ) $となっています。
    これは非常に小さい値であり、関数の理論的な最小値に非常に近いことを示しています。

グラフの説明

グラフは評価関数の値をカラーマップとしてプロットしたものです。
以下のような特徴があります：

• カラーマップ:

  • 色の濃淡で関数の値を表しています。

  濃い色の部分が関数の値が低い（小さい）領域を示し、薄い色の部分が関数の値が高い（大きい）領域を示します。

• 等高線:

  • 関数の等高線をプロットしています。

  等高線は、同じ関数値を持つ点を結んだ線であり、最小値に向かって収束するように見えます。

• 最適解のプロット:

  • 赤い点で最適解を示しています。
    この点が$ ( (2.99999768, 2.00000504) ) $の位置にあります。
    これにより、最適化によって見つけた最適解がグラフ上のどこにあるかが視覚的にわかります。

食事計画（線形計画問題）

CVXPYを使って線形計画問題を解きます。

ここでは、食事計画の問題を考えます。

この問題では、複数の食品から適切な組み合わせを選んで、特定の栄養要件を満たしつつ、コストを最小限に抑えることを目的とします。

問題設定

食品の種類：

1. チキン (Chicken)
2. 牛肉 (Beef)
3. 豆 (Beans)

各食品のコストと栄養素含有量は以下の通り：

• チキン: コスト 2ドル、タンパク質 20g、脂肪 5g、炭水化物 0g
• 牛肉: コスト 3ドル、タンパク質 15g、脂肪 10g、炭水化物 0g
• 豆: コスト 1ドル、タンパク質 10g、脂肪 2g、炭水化物 20g

栄養要件：

• タンパク質: 最低 30g
• 脂肪: 最低 10g、最大 20g
• 炭水化物: 最低 20g

解法

この問題をCVXPYを使って解きます。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

import cvxpy as cp
import numpy as np

# 各食品のコストと栄養素含有量
cost = np.array([2, 3, 1])
protein = np.array([20, 15, 10])
fat = np.array([5, 10, 2])
carbs = np.array([0, 0, 20])

# 栄養要件
min_protein = 30
min_fat = 10
max_fat = 20
min_carbs = 20

# 食品の量 (変数)
x = cp.Variable(3, nonneg=True)

# コスト最小化
objective = cp.Minimize(cost @ x)

# 制約条件
constraints = [
    protein @ x >= min_protein,
    fat @ x >= min_fat,
    fat @ x <= max_fat,
    carbs @ x >= min_carbs
]

# 問題の定義と解決
problem = cp.Problem(objective, constraints)
problem.solve()

# 結果の表示
print(f"Status: {problem.status}")
print(f"Optimal value: {problem.value:.2f} dollars")
print(f"Optimal solution: {x.value}")
print(f"Chicken: {x.value[0]:.2f} units")
print(f"Beef: {x.value[1]:.2f} units")
print(f"Beans: {x.value[2]:.2f} units")

このコードでは、以下の手順で食事計画問題を解きます：

1. 各食品のコストと栄養素含有量を定義します。
2. 栄養要件を設定します。
3. 変数 x を定義し、各食品の量を表します（非負制約）。
4. 目的関数をコストの最小化として定義します。
5. 栄養要件に基づく制約を設定します。
6. 問題を定義し、解決します。
7. 最適なコストと食品の量を表示します。

このコードを実行すると、栄養要件を満たしつつコストを最小限に抑える最適な食品の組み合わせが得られます。

[実行結果]

Status: optimal
Optimal value: 3.72 dollars
Optimal solution: [0.64 0.48 1.  ]
Chicken: 0.64 units
Beef: 0.48 units
Beans: 1.00 units

ソースコード解説

ソースコードの詳細は以下の通りです。

1. ライブラリのインポート

1
2

import cvxpy as cp
import numpy as np

ここでは、最適化問題を解くためのCVXPYライブラリと、数値計算を行うためのNumPyライブラリをインポートしています。

2. 各食品のコストと栄養素含有量の定義

1
2
3
4

cost = np.array([2, 3, 1])
protein = np.array([20, 15, 10])
fat = np.array([5, 10, 2])
carbs = np.array([0, 0, 20])

ここでは、各食品（チキン、ビーフ、豆）のコストと栄養素（タンパク質、脂肪、炭水化物）の含有量を配列として定義しています。

例えば、チキンのコストは2ドルで、タンパク質が20グラム、脂肪が5グラム含まれています。

3. 栄養要件の定義

1
2
3
4

min_protein = 30
min_fat = 10
max_fat = 20
min_carbs = 20

ここでは、最低限必要なタンパク質、脂肪の最小および最大量、最低限必要な炭水化物の量を定義しています。

4. 変数の定義

1

x = cp.Variable(3, nonneg=True)

ここでは、最適化問題の変数である各食品の量を表すベクトル x を定義しています。
この変数は非負（負の値を取らない）であることが指定されています。

5. コスト最小化の目的関数

1

objective = cp.Minimize(cost @ x)

ここでは、総コストを最小化する目的関数を定義しています。
cost @ x はコストと食品の量の内積を計算し、これを最小化します。

6. 制約条件の定義

1
2
3
4
5
6

constraints = [
    protein @ x >= min_protein,
    fat @ x >= min_fat,
    fat @ x <= max_fat,
    carbs @ x >= min_carbs
]

ここでは、栄養要件に基づく制約条件を定義しています。
具体的には、次の制約を課しています：

• 総タンパク質が30グラム以上
• 総脂肪が10グラム以上20グラム以下
• 総炭水化物が20グラム以上

7. 最適化問題の定義と解決

1
2

problem = cp.Problem(objective, constraints)
problem.solve()

ここでは、目的関数と制約条件をもとに最適化問題を定義し、これを解決しています。
problem.solve() によって、最適解が計算されます。

8. 結果の表示

1
2
3
4
5
6

print(f"Status: {problem.status}")
print(f"Optimal value: {problem.value:.2f} dollars")
print(f"Optimal solution: {x.value}")
print(f"Chicken: {x.value[0]:.2f} units")
print(f"Beef: {x.value[1]:.2f} units")
print(f"Beans: {x.value[2]:.2f} units")

ここでは、最適化のステータス、最適なコスト、各食品の最適な量を表示しています。

結果解説

[実行結果]

Status: optimal
Optimal value: 3.72 dollars
Optimal solution: [0.64 0.48 1.  ]
Chicken: 0.64 units
Beef: 0.48 units
Beans: 1.00 units

• Status: optimal:
  問題が最適に解決されたことを示しています。
• Optimal value: 3.72 dollars:
  最適な食品の組み合わせのコストが3.72ドルであることを示しています。
• Optimal solution:
  各食品の最適な量を示しています。
  具体的には、チキン0.64単位、ビーフ0.48単位、豆1.00単位です。

これにより、指定された栄養要件を満たしつつ、コストを最小限に抑えるための最適な食事計画が得られます。

巡回セールスマン問題（Traveling Salesman Problem, TSP）

最適化問題の一例として、「巡回セールスマン問題（Traveling Salesman Problem, TSP）」を挙げます。

TSPは、いくつかの都市を訪問する最短経路を求める問題で、非常に計算困難です。

今回は、Pythonを使ってTSPを解き、結果をグラフ化します。

巡回セールスマン問題の説明

巡回セールスマン問題は、以下のように定義されます：

• あるセールスマンが$N$個の都市を訪れ、それぞれの都市を一度だけ訪問し、出発地点に戻る必要がある。
• すべての都市間の距離が与えられている。
• セールスマンが移動する総距離を最小化する経路を見つけることが目的。

解法

TSPはNP困難問題であり、大規模な問題を厳密に解くのは現実的ではありません。
ここでは、近似解法の一つである遺伝的アルゴリズム（Genetic Algorithm）を用いて解を求めます。

実装

まず、必要なライブラリをインストールします。

1

pip install deap matplotlib numpy

次に、Pythonコードを以下に示します：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

import numpy as np
import matplotlib.pyplot as plt
from deap import base, creator, tools, algorithms

# 都市数
num_cities = 20

# ランダムな都市の座標を生成
np.random.seed(42)
cities = np.random.rand(num_cities, 2)

# 距離行列を計算
distance_matrix = np.sqrt(((cities[:, np.newaxis] - cities)**2).sum(axis=2))

# 遺伝的アルゴリズムの設定
creator.create("FitnessMin", base.Fitness, weights=(-1.0,))
creator.create("Individual", np.ndarray, fitness=creator.FitnessMin)

toolbox = base.Toolbox()
toolbox.register("indices", np.random.permutation, num_cities)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.indices)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)

def evalTSP(individual):
    distance = 0
    for i in range(num_cities):
        distance += distance_matrix[individual[i-1], individual[i]]
    return distance,

toolbox.register("mate", tools.cxOrdered)
toolbox.register("mutate", tools.mutShuffleIndexes, indpb=0.05)
toolbox.register("select", tools.selTournament, tournsize=3)
toolbox.register("evaluate", evalTSP)

def main():
    population = toolbox.population(n=300)
    ngen = 400
    cxpb = 0.7
    mutpb = 0.2

    result, log = algorithms.eaSimple(population, toolbox, cxpb, mutpb, ngen, 
                                      stats=None, halloffame=None, verbose=False)
    
    best_ind = tools.selBest(population, 1)[0]
    return best_ind

best_route = main()

# 結果をプロット
plt.figure(figsize=(10, 5))
plt.scatter(cities[:, 0], cities[:, 1], color='red')
for i in range(num_cities):
    plt.annotate(i, (cities[i, 0], cities[i, 1]))
route = np.append(best_route, best_route[0])
plt.plot(cities[route, 0], cities[route, 1], 'b-')
plt.title('Traveling Salesman Problem - Best Route')
plt.xlabel('X Coordinate')
plt.ylabel('Y Coordinate')
plt.grid(True)
plt.show()

コードの説明

1. 都市の生成:

   • num_citiesを設定し、ランダムな都市の座標を生成します。
   • 都市間の距離行列を計算します。

2. 遺伝的アルゴリズムの設定:

   • DEAPライブラリを使用して遺伝的アルゴリズムを設定します。
   • creatorで個体（経路）とその適合度を定義します。
   • toolboxで個体の生成、交叉、突然変異、選択、および評価関数を登録します。

3. 適合度関数:

   • evalTSP関数で個体（経路）の総距離を計算します。

4. 主関数:

   • 遺伝的アルゴリズムの主要なパラメータを設定し、eaSimple関数を使用して進化を実行します。
   • 最良の経路を選択し、結果を返します。

5. 結果のプロット:

   • 最良の経路をプロットし、都市の座標と経路を視覚化します。

結果

このコードを実行すると、TSPの最良の経路がプロットされます。

[実行結果]

都市間の最短経路が青線で表示され、各都市の座標が赤点で示されます。

双曲放物面（hyperbolic paraboloid）

双曲放物面（hyperbolic paraboloid）は、特定の二次曲面で、鞍型（saddle shape）として知られる形状を持っています。

これは幾何学的に興味深い構造を持つため、建築や土木工学などさまざまな分野で応用されています。

双曲放物面の方程式

双曲放物面は次の一般形の二次方程式で表されます：

$$
z = \frac{x^2}{a^2} - \frac{y^2}{b^2}
$$

ここで、$(a) $と$ (b) $は正の実数であり、曲面の形状を定義します。
特に、双曲放物面は放物線と双曲線の特性を組み合わせたものです。

特徴と性質

1. 鞍型:

   • 双曲放物面の形状は「鞍型」とも呼ばれ、中心点の周りで異なる曲率を持ちます。
     片方の軸に沿っては上に開いた放物線の形を持ち、もう片方の軸に沿っては下に開いた放物線の形を持ちます。
   • 中心点（原点）では、曲面は凹型と凸型が交互に現れ、典型的な鞍のような形状を形成します。

2. 双曲線と放物線の交差:

   • 双曲放物面は、$x$軸に沿っては放物線$ ( z = \frac{x^2}{a^2} ) $の形状を持ち、$y$軸に沿っては放物線$ ( z = -\frac{y^2}{b^2} ) $の形状を持ちます。
   • 任意の平行断面（$z$ = 定数）の形状は双曲線となります。

3. 無限に広がる曲面:

   • 双曲放物面は無限に広がる曲面であり、$x$軸や$y$軸の方向に制限なく広がります。

4. 曲率:

   • 双曲放物面の曲率は負であり、これは曲面が中心点の周りで異なる方向に曲がっていることを意味します。

実生活での応用

双曲放物面はその構造的な強度と美しさから、建築や土木工学で広く使用されています。

以下はそのいくつかの応用例です：

1. 建築:

   • モダンな建築物や屋根構造で、双曲放物面はしばしば使用されます。
     例えば、シドニーオペラハウスの屋根の形状は双曲放物面を基にしています。

2. 橋梁:

   • 双曲放物面の形状は橋のデザインにも応用され、構造的な効率性と美しさを兼ね備えたデザインが可能となります。

3. インフラストラクチャー:

   • 双曲放物面はパビリオン、シェル構造、パラボラアンテナなどにも利用されます。
     特に、シェル構造は軽量でありながら高い強度を持ちます。

以下のコードでは、双曲放物面の形状を描き、カラフルなカラーマップを適用します：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# パラメータの設定
u = np.linspace(-2, 2, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

# 放物面の方程式
x = u
y = v
z = u**2 - v**2

# 3Dプロットの作成
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 放物面の描画
surf = ax.plot_surface(x, y, z, cmap='coolwarm', edgecolor='none')

# カラーバーの追加
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)

# ラベルとタイトルの設定
ax.set_xlabel('X Axis')
ax.set_ylabel('Y Axis')
ax.set_zlabel('Z Axis')
ax.set_title('3D Hyperbolic Paraboloid')

# 視点の設定
ax.view_init(elev=45, azim=60)

plt.show()

ソースコード解説

1. ライブラリのインポート:

   • numpyは数値計算を行うために使用します。
   • matplotlib.pyplotはグラフ描画のために使用します。
   • mpl_toolkits.mplot3dは3Dプロットを描画するために使用します。

2. パラメータの設定:

   • uとvは$-2$から$2$までの範囲で等間隔に$100$個の点を生成します。
   • np.meshgridは、2つの1次元配列から2次元の格子を生成します。

3. 放物面の方程式:

   • x, y, zは放物面の座標を表します。
     放物面の方程式は$z = u^2 - v^2$です。

4. 3Dプロットの作成:

   • plt.figure(figsize=(10, 8))で新しい図を作成し、figに割り当てます。
     figsizeで図のサイズを指定します。
   • fig.add_subplot(111, projection='3d')で3Dサブプロットを作成し、axに割り当てます。

5. 放物面の描画:

   • ax.plot_surface(x, y, z, cmap='coolwarm', edgecolor='none')で放物面を描画します。
     cmapはカラーマップを指定し、edgecolor='none'でエッジの色を無効にします。

6. カラーバーの追加:

   • fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)でカラーバーを追加し、色の範囲を視覚化します。

7. ラベルとタイトルの設定:

   • ax.set_xlabel, ax.set_ylabel, ax.set_zlabelで各軸のラベルを設定します。
   • ax.set_titleで図のタイトルを設定します。

8. 視点の設定:

   • ax.view_init(elev=45, azim=60)で3Dプロットの視点を設定します。
     elevは垂直方向の角度、azimは水平方向の角度を指定します。

9. プロットの表示:

   • plt.show()でプロットを表示します。

このコードを実行することで、3Dの放物面がよりカラフルに、美しく描画されます。
カラーマップと視点を工夫することで、視覚的に非常に魅力的なグラフを作成できます。

グラフ解説

[実行結果]

このコードを実行すると、上記のような美しい3Dの放物面が表示されます：

双曲放物面の形状:

$z = u^2 - v^2$に従って計算された双曲放物面が描画されます。
この形状は鞍型で、特定の曲率を持っています。

カラーマップ:

高さに基づいて色が変化するため、放物面の形状が視覚的に強調されます。
coolwarmカラーマップは青から赤へのグラデーションを作成し、見栄えが良くなります。

カラーバー:

放物面の高さに対応する色の範囲が示されるため、特定の高さがどの色に対応するかが一目でわかります。

軸ラベルとタイトル:

$x$軸、$y$軸、$z$軸のラベルとグラフのタイトルが表示され、グラフの内容が明確になります。

• 視点の設定:
  適切な視点から放物面を観察できるため、形状とカラーマップが立体的に見えます。

このグラフは、数学的な関数の視覚化、特に双曲放物面の形状と特性を示すのに非常に有用です。