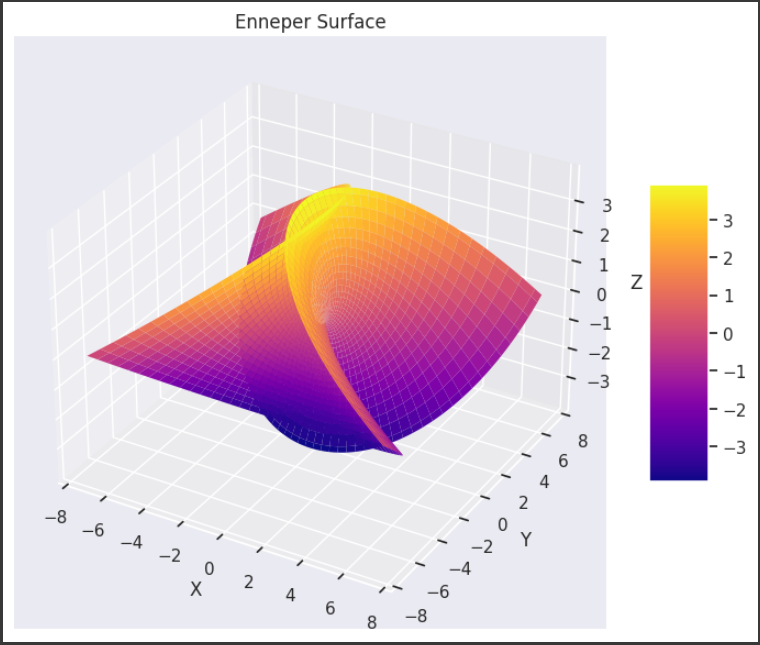
エンネーパーの面（Enneper Surface）

エンネーパーの面（Enneper Surface）

エンネーパーの面（Enneper Surface）は、微分幾何学における特異な極小曲面の一例であり、以下の特徴を持ちます：

特徴

  1. 極小曲面：

    • エンネーパーの面は、曲面上の任意の点で曲率が最小となる極小曲面です。
      極小曲面は、物理的には石鹸膜のように、表面積を最小化する形状を取る面です。

  2. 自己交差：

    • エンネーパーの面は、自己交差する点を持ちます。
      つまり、曲面の一部が別の部分と交差する点が存在します。

  3. パラメトリック方程式：

    • エンネーパーの面は、以下のパラメトリック方程式で定義されます：
      $$
      x(u, v) = u - \frac{u^3}{3} + u v^2
      $$
      $$
      y(u, v) = v - \frac{v^3}{3} + v u^2
      $$
      $$
      z(u, v) = u^2 - v^2
      $$
      ここで、$(u) $と$ (v) $はパラメータです。

  4. 対称性：

    • エンネーパーの面は、対称性を持つ曲面であり、中心対称的な形状をしています。
      曲面は中央部分から外側に向かって曲がりくねる形状を持ち、対称的に広がります。

  5. 幾何学的美しさ：

    • エンネーパーの面は、その複雑で滑らかな形状から、数学的にも美しい曲面として知られています。

例

エンネーパーの面は、数学的研究や教育においてよく使用される曲面で、極小曲面の典型例として知られています。

コンピュータグラフィックスや芸術的なデザインにおいても、その独特の形状が利用されることがあります。

視覚的な説明

エンネーパーの面を視覚化すると、以下のような特徴が見られます：

  • 曲面は中央部で交差し、内側にくびれた形状を形成します。
  • 高さの違いによって色が変わるカラーマップを適用することで、曲面の高低差が視覚的に強調されます。

エンネーパーの面は、その独特の形状と数学的特性から、微分幾何学における重要な研究対象の一つです。

プログラム例

以下にPythonコードを示します。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns

# seabornのスタイルを使用
sns.set(style='darkgrid')

# パラメータの範囲を設定
u = np.linspace(-2, 2, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

# エンネーパーの面のパラメトリック方程式
x = u - (u**3) / 3 + u * v**2
y = v - (v**3) / 3 + v * u**2
z = u**2 - v**2

# プロットを作成
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')

# 3Dサーフェスプロット
surf = ax.plot_surface(x, y, z, cmap='plasma', edgecolor='none')

# カラーバーを追加
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)

# 軸ラベル
ax.set_xlabel('X軸')
ax.set_ylabel('Y軸')
ax.set_zlabel('Z軸')

# タイトルを追加
ax.set_title('Enneper Surface')

# グラフを表示
plt.show()

このコードを実行すると、エンネーパーの面の3Dプロットが描画されます。

学術的に興味深い形状を持つエンネーパーの面を使って、複雑な3Dグラフを表示します。

[実行結果]

ソースコード解説

ソースコードを詳しく説明します。

1. 必要なライブラリのインポート

1
2
3
4
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns

このセクションでは、以下のライブラリをインポートしています。

  • numpy: 数値計算を効率的に行うためのライブラリ。
  • matplotlib.pyplot: グラフ作成のためのライブラリ。
  • mpl_toolkits.mplot3d: 3Dプロットをサポートするためのライブラリ。
  • seaborn: 見栄えの良いグラフを作成するためのライブラリ。

2. Seabornスタイルの設定

1
2
# seabornのスタイルを使用
sns.set(style='darkgrid')

Seabornのスタイルをdarkgridに設定しています。
これにより、プロットの背景がダークグリッドスタイルになります。

3. パラメータの範囲を設定

1
2
3
4
# パラメータの範囲を設定
u = np.linspace(-2, 2, 100)
v = np.linspace(-2, 2, 100)
u, v = np.meshgrid(u, v)

ここでは、uとvの範囲を-2から2まで$100$等分した配列を作成しています。
その後、np.meshgridを使用して2次元のグリッドデータを作成しています。

4. エンネーパーの面のパラメトリック方程式

1
2
3
4
# エンネーパーの面のパラメトリック方程式
x = u - (u**3) / 3 + u * v**2
y = v - (v**3) / 3 + v * u**2
z = u**2 - v**2

エンネーパーの面のパラメトリック方程式を使って、x, y, zの座標を計算しています。

5. プロットの作成

1
2
3
# プロットを作成
fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')

figオブジェクトを作成し、サイズを設定しています。
次に、3Dプロット用のaxオブジェクトを追加しています。

6. 3Dサーフェスプロット

1
2
# 3Dサーフェスプロット
surf = ax.plot_surface(x, y, z, cmap='plasma', edgecolor='none')

ax.plot_surfaceを使用して、x, y, zのデータを基に3Dサーフェスプロットを作成しています。
色のマッピングにはplasmaカラーマップを使用し、エッジの色を無くしています。

7. カラーバーの追加

1
2
# カラーバーを追加
fig.colorbar(surf, ax=ax, shrink=0.5, aspect=5)

サーフェスプロットに対応するカラーバーを追加しています。
shrinkでカラーバーのサイズを調整し、aspectでアスペクト比を設定しています。

8. 軸ラベルの設定

1
2
3
4
# 軸ラベル
ax.set_xlabel('X軸')
ax.set_ylabel('Y軸')
ax.set_zlabel('Z軸')

3Dプロットの各軸にラベルを設定しています。

9. タイトルの追加

1
2
# タイトルを追加
ax.set_title('Enneper Surface')

3Dプロットにタイトルを追加しています。

10. グラフの表示

1
2
# グラフを表示
plt.show()

最終的に、plt.show()を使用してグラフを表示しています。

以上が、コードの詳細な説明です。

各ステップがどのように3Dプロットを作成するために機能しているかを理解することで、同様の3Dプロットを作成する際に応用することができます。

結果解説

[実行結果]

このグラフは、エンネーパーの面（Enneper Surface）を3Dで表示したものです。

エンネーパーの面は、数学や幾何学で知られる特異な曲面で、以下のような特徴を持っています：

1. 形状：

エンネーパーの面は、曲線的で非線形な形状を持ち、複雑な対称性を示します。
表面は中央部から外側に向かって曲がりくねり、波打つような形状になっています。

2. カラーマップ：

plasmaというカラーマップが使用されており、表面の高さや深さに応じて色が変化します。
これにより、3D構造の高低差が視覚的にわかりやすくなっています。

3. 軸：

  • X軸：横方向の軸。
  • Y軸：縦方向の軸。
  • Z軸：高さ方向の軸。

4. カラーバー：

グラフの右側にカラーバーが表示されており、色と高さの対応関係を示しています。
これにより、特定の色がどの高さを表しているかがわかります。

このグラフは、エンネーパーの面の複雑な幾何学的特徴を直感的に理解できるように可視化しています。