非線形計画法（Nonlinear Programming、NLP）

非線形計画法（Nonlinear Programming、NLP）

非線形計画法（Nonlinear Programming、NLP）は、目的関数と制約条件が非線形となる最適化問題を扱います。

今回は、非線形最適化の典型的な例題として、以下の問題を考えます。

例題

最小化する関数と条件は以下の通りです。

minimize f(x,y)=(x−1)2+(y−1)2

制約条件:

g1(x,y)=x2+y2−1≤0


g2(x,y)=x≥0

g3(x,y)=y≥0

この問題をPythonのscipy.optimizeを使って解き、その結果をグラフ化します。

必要なライブラリのインストール

Google Colab環境で以下のコマンドを実行して必要なライブラリをインストールします。

1
!pip install scipy matplotlib

コード

以下がこの問題を解き、その結果をグラフ化するPythonコードです。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 最適化する関数の定義
def objective_function(x):
    return (x[0] - 1)**2 + (x[1] - 1)**2

# 制約条件の定義
def constraint1(x):
    return 1 - (x[0]**2 + x[1]**2)  # x^2 + y^2 <= 1 に対応

# 境界条件の定義
bounds = [(0, None), (0, None)]  # x >= 0, y >= 0

# 制約条件のリスト
constraints = [{'type': 'ineq', 'fun': constraint1}]

# 初期点
x0 = [0.5, 0.5]

# 最適化の実行
result = minimize(objective_function, x0, method='SLSQP', bounds=bounds, constraints=constraints)

# 結果の出力
print('最適解:', result.x)
print('最小値:', result.fun)

# 結果のグラフ化
x = np.linspace(-0.5, 1.5, 400)
y = np.linspace(-0.5, 1.5, 400)
X, Y = np.meshgrid(x, y)
Z = (X - 1)**2 + (Y - 1)**2

plt.contour(X, Y, Z, levels=30)
plt.plot(result.x[0], result.x[1], 'ro', label='Optimal Point')  # 最適解を赤い点でプロット

# 制約条件の境界線をプロット
theta = np.linspace(0, 2*np.pi, 100)
x_circle = np.cos(theta)
y_circle = np.sin(theta)
plt.plot(x_circle, y_circle, 'b-', label='$x^2 + y^2 \leq 1$')

plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1.5)
plt.xlabel('x')
plt.ylabel('y')
plt.title('Nonlinear Programming Optimization')
plt.grid(True)
plt.legend()
plt.fill_between(x_circle, y_circle, 1.5, where=(y_circle >= 0), alpha=0.3, color='gray')  # 可行領域
plt.show()

解説

  1. 最適化する関数の定義:
    目的関数 (f(x,y)=(x−1)2+(y−1)2)を定義します。

  2. 制約条件の定義:
    非線形制約 (g1(x,y)=x2+y2−1≤0)を定義します。

  3. 境界条件の定義:
    (x≥0)および(y≥0)に対応する境界条件を定義します。

  4. 制約条件のリスト constraints:
    制約条件をリスト形式で定義します。

  5. 初期点の設定 x0:
    最適化アルゴリズムの初期点を設定します。

  6. 最適化の実行 result:
    scipy.optimize.minimize を使用して最適化を実行します。
    methodにはSLSQP（Sequential Least Squares Programming）を使用します。

  7. 結果の出力:
    得られた最適解と最小値を表示します。

  8. グラフ化:

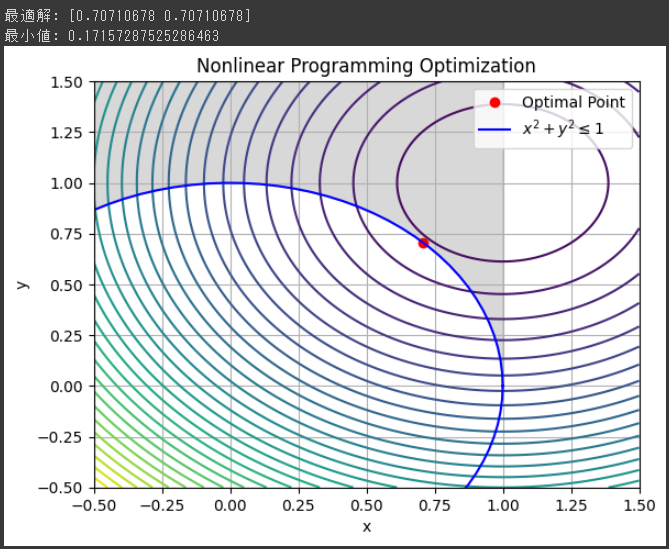
    • 目的関数の等高線を描画。
    • 制約条件 (x2+y2≤1)の境界線を描画。
    • 最適解を赤い点でプロット。
    • 制約条件を満たす領域を灰色で塗りつぶします。

以上で、非線形最適化問題の解と制約条件を含む結果をグラフで視覚的に確認できます。

実行結果